お茶の水女子大学・大学院人間文化創成科学研究科・人間科学系
（人間発達科学専攻・応用社会学コース担当）

1. 超初心者向けのRインストールガイド

1. 基本演算とヴェクトル・行列，データ・フレイムの作成
2. 確率分布を読み取ったりグラフに描いたりする方法
3. 欠損値，変数のリコード
4. 一つのカテゴリカル変数の度数分布表の作成
5. 多項選択回答の表の作成
6. 分割表（クロス表）の作成

二変数の分割表（クロス表）

　調査結果の報告においては，高度な分析をするだけではなく，収集した情報の基本的な集計結果を示す事も重要になる。しかしRでは，度数分布表（単純集計表などとも呼ばれる）や分割表（連関表，クロス表）について，必要最低限の結果を出力するコマンドが基本で，色々な情報を纏めて提示する為には自分で少し手を加える必要がある。
　以下では，学部学生の演習レヴェルであると便利だと思われる作表方法を紹介する。

模擬データの作成

　以下は，二つの変数（5件法と4件法，NA混じり）を発生させて，それを（敢えて）データ・フレイムにしている。何故敢えてデータ・フレイムにしているかと言えば，通常社会調査データはcsvファイルでデータを作成し，それをデータ・フレイムとしてRに読み込んで分析するので，それに近い状態を再現する為である。 　それぞれの変数にアクセスする為には，data01$q1，data01$q2とする事になる。

二つのカテゴリカル変数の分割表（クロス表）

　社会学でクロス表と呼ぶ事の多い分割表（連関表; contingency table）は二つのカテゴリカル変数の集計表であるが，これを作成するRの関数も table( ) である。table( ) に二つの変数を引数で与えると二変数の分割表になる。一変数の場合と同じく，useNA=オプションを指定しないとNAを除外した表になる。
　table( ) で作成した分割表は表の本体だけであるが，集計結果を示す場合には，行周辺度数・列周辺度数なども併せて表示する。table( ) で作成された分割表が t01 と云うオブジェクトに格納されているとすると，周辺度数を付加した表は，addmargins( ) 関数にt01を引数として与えれば作成される。
　大抵の場合，度数ではなく相対度数の表も作成したい。関数は一変数の時と同じ prop.table( ) 関数である。何もオプションを付けないと全体％の表になり，margin=1 と云うオプションを付けると行％の表になる。margin=2 では列％の表である。
　以上を例示する。オブジェクト名は適当であり，自由に付けてよい。


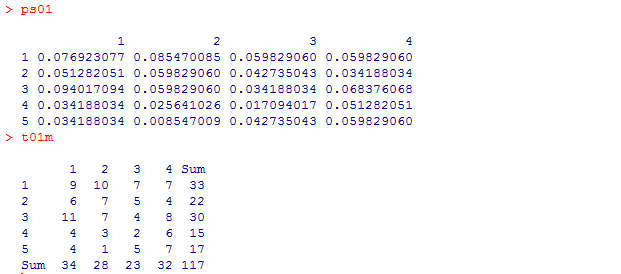
　これらの結果から必要な情報を抜き出して合成し，一つの表にしてみよう。以下はちょっと難しいので初学者は解読出来なくても良い。
　一変数の時に作成した新関数 freq.table( ) と同様に，この長いスクリプトを新関数として定義してしまうと，繰り返して使用するのに便利である。二つの変数を引数とする新関数 contingency( , ) を定義しよう。
　この関数に q1，q2 を引数として与えた結果が以下である（以下のスクリーンショットではうっかり失念しているが，データ・フレイム化している場合には，data01$q1，data01$q2 などとして引数に与える）。関数の結果を一旦 result と云うオブジェクトに格納してから表示している。最後に，分割表のカイ二乗検定の結果とクラメールのVも計算して出力している。


　違う変数を生成して関数に与えてみた。NAは無視して作表される。


　NAを含んだ分割表について同様の作表をしたい場合には，新関数の定義の冒頭の t01 <- table(x, y) を t01 <- table(x, y, useNA="ifany") に変えると出来る。関数名は変えた方が良いだろう。以下がその例である。新関数名を contingencyNA( ) として，上と同じ q3，q4を引数として与えている。


　せっかく作表した結果をcsvファイルに保存するには，以下の様にする。新関数の結果をlist形式で出力しているので，そのうち最初の成分だけを [[1]] で指定している。因みに第二成分はカイ二乗検定の結果とクラマーのVである。

集計表の項目ラベル

　SPSSでは変数に変数ラベル，値に値ラベルを定義する事が出来，出力を見易くする事が出来るが，Rはこの点については余り親切ではない。もっとも特に値ラベルについては，実体としての数値が何であるかが分からなくなって却って初心者が間違える場合もあるので，うまく付けないと（或いは適切に表示オプションを設定しないと）便利ではなくなる。
　いずれにせよRでも出力を分かり易くする方法は知っておいた方が良いので，ここでは分割表にラベルを付ける単純な方法を紹介する。上の新関数 contingency( , ) では使えないものもあるので注意。
　まずは模擬データを生成する。 　このデータで，性別の度数分布表や，性別と教育年数の分割表を作成すると次の様になる。

SPSSの様な変数ラベルや値ラベルがついていないので，これだけでは何であるか分からない。
まずは，性別の度数分布表をオブジェクトに格納して，値ラベル(value label)を付けてみよう。

　これで情報が読み取り易くなったが，依然として変数ラベル(variable label)は付いていない。変数ラベルを付けるには次の様にする。
　これと同様にして，分割表の行と列にもラベルを付けよう。


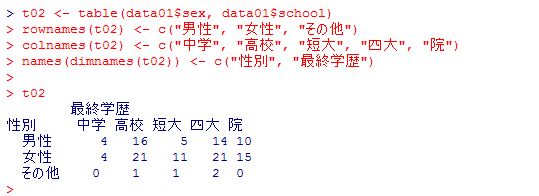
　変数そのものにラベルを貼り付けるのとは違って集計表の行や列に名前を付けているだけなので，正直このやり方ではいちいち非常に面倒であり，SPSS的な変数ラベル，値ラベルを使いたいと思う事も多いだろう。しかしそこは逆に，常に値とラベルの対応に注意させられる事で，ラベルに惑わされて実態としての値（数字）を取り違え，処理や解釈を誤ると云うリスクがなくなると前向きに考えておこう（実際初心者がSPSSを使う場合にこのリスクは小さくない）。Rで変数ラベル，値ラベルを使用可能にする工夫も幾つか開発されているが（例えば"labelled"パッケイジなど），ここでは極力追加アプリケイションや追加パッケイジをインストールしなくて済む方法を紹介しようとしているので，割愛する。