統計的推測(statistical inference)
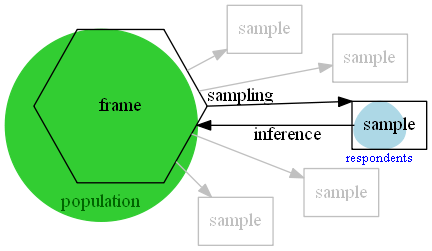
標本抽出分布(sampling distribution)
年収についての模擬母集団データファイル:ダウンロード
| 母集団分布の確認 |
|---|
| R script |
data01 <- read.csv("mock_income.csv")
hist(data01$income, freq=TRUE, ylab="人数", breaks=seq(0, 2000, by=50 ),
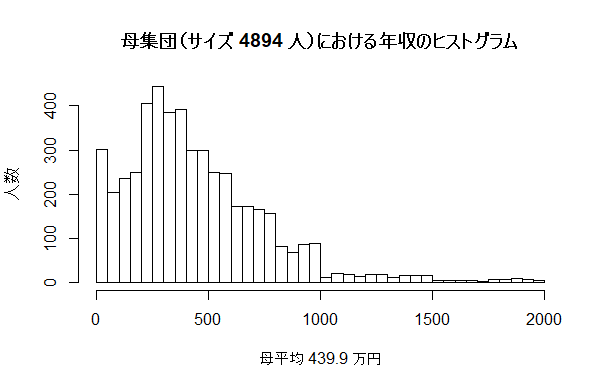
main=paste("母集団(サイズ", nrow(data01), "人)における年収のヒストグラム"),
xlab=paste("母平均", round(mean(data01$income), 1), "万円"))
|
| R Graphics |
 |
| 一つの標本の分布と母平均の点推定 | ||||
|---|---|---|---|---|
| R script | ||||
n1 <- 200
sample02 <- sample(data01$income, size=n1)
m1 <- mean(sample02); sd1 <- sd(sample02)
m1
hist(sample02, freq=TRUE, ylab="人数", breaks=seq(0, 2000, by=50),
main=paste("ある標本(サイズ", n1,"人)における年収のヒストグラム\n"),
xlab=paste("万円(標本平均", round(m1, 1), "万円)"))
|
| 標本抽出実習 |
|---|
| R script |
times <- 10000 # 抽出回数の指定
n <- 50 # サンプルサイズの指定
sample_mean <- vector(length=times)
for (i in 1:times) {
temp_sample <- sample(data01$income, n)
sample_mean[i] <- mean(temp_sample)
}
hist(sample_mean, freq=TRUE, ylab="標本の数",
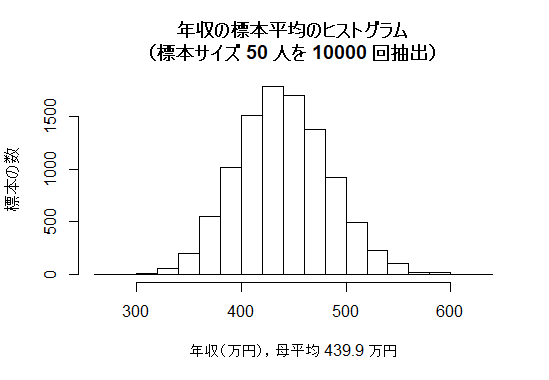
main=paste("年収の標本平均のヒストグラム\n(標本サイズ", n, "人を", times, "回抽出)"),
xlab=paste("年収(万円),母平均", round(mean(data01$income), 1), "万円"))
|
| R Graphics |
 |
区間推定(interval estimation)
一つの標本を抽出し,標本平均と不偏分散を求め,信頼区間を求める。
| 一つの標本による母平均の区間推定 | ||
|---|---|---|
| R script | ||
n1 <- 200 # 標本サイズを指定 p1 <- .90 # 信頼水準を指定 sample02 <- sample(data01$income, size=n1) m1 <- mean(sample02); sd1 <- sd(sample02) alpha <- qt(0.5+p1/2, df=n1-1) # 臨界値を算出 N <- nrow(data01) # 母集団サイズを算出 se <- sqrt((N-n1)/(N-1))*sd1/sqrt(n1) # 標準誤差を算出 N; n1; m1; sd1; alpha; se m1 + c(-1, 1)*alpha*se # p1%信頼区間の下限と上限 |
| 信頼区間シミュレイション |
|---|
| R script[2018.05.18修正] |
times <- 20 # 抽出回数の指定
n2 <- 200 # サンプルサイズの指定
N <- nrow(data01)
sample_mean <- vector(length=times)
sample_sd <- vector(length=times)
uplimit <- vector(length=times) # 信頼区間上限のヴェクトル
lowlimit <- vector(length=times) # 信頼区間下限のヴェクトル
# times回だけ以下の標本抽出と標本統計量の計算の操作を繰り返す
for (i in 1:times) {
temp_sample <- sample(data01$income, n2)
sample_mean[i] <- mean(temp_sample)
sample_sd[i] <- sd(temp_sample)
}
# ここから先だけを,pの値を変えて繰り返す事が出来る
p <- .90 # 信頼水準の設定
alpha <- qt((1-p)/2, df=n2-1, lower.tail=FALSE) # 限界値の計算
# 信頼区間の上限と下限の計算
uplimit <- sample_mean + alpha*sqrt((N-n2)/(N-1))*sample_sd/sqrt(n2)
lowlimit <- sample_mean - alpha*sqrt((N-n2)/(N-1))*sample_sd/sqrt(n2)
windows(width=5, height=5) # グラフウィンドウの大きさの指定
plot(sample_mean, c(1:times), bty="l", las=1, xlim=c(360, 520),
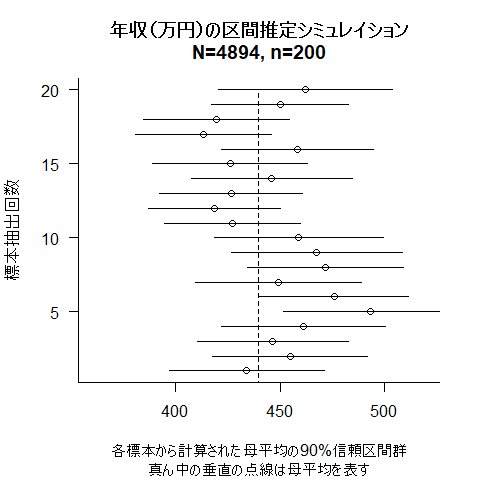
sub="真ん中の垂直の点線は母平均を表す", ylab="標本抽出回数",
xlab=sprintf("各標本から計算された母平均の%.0f%%信頼区間群", p*100),
main=sprintf("年収(万円)の区間推定シミュレイション\nN=%d, n=%d", N, n2))
segments(lowlimit, c(1:times), uplimit, c(1:times))
segments(mean(data01$income), 0, mean(data01$income), times, lty=2)
|
| R Graphics |
 |
母平均の区間推定と線形回帰アプローチ
| 一標本による母平均の区間推定(再掲)と線形モデル |
|---|
| R script |
# 母平均の区間推定(手計算) n1 <- 200 p1 <- .90 sample02 <- sample(data01$income, size=n1) m1 <- mean(sample02); sd1 <- sd(sample02) alpha <- qt(0.5+p1/2, df=n1-1) N <- nrow(data01) fpc <- sqrt((N-n1)/(N-1)) se <- sd1/sqrt(n1) m1; alpha; se m1 + c(-1, 1)*alpha*fpc*se # 有限母集団修正項付き m1 + c(-1, 1)*alpha*se # 有限母集団修正項無し reg0 <- lm(sample02 ~ 1) # 定数項(切片のみ)の回帰モデル confint(reg0, level=0.9) summary(reg0) |
| R console |
 |
統計的検定(statistical test),ゼロ仮説有意性検定(NHST)
①(母集団についての)ゼロ仮説を正しいものと仮定
②「あまりにも稀すぎるので何かがおかしい」と判断する境目の確率である有意水準を設定
③ゼロ仮説の下で,何らかの既知の確率分布に従うと考えられる検定統計量を標本データから計算し,偶然にそのような値になる確率(有意確率)を求める
④有意確率が有意水準よりも小さければ,そんな稀なことが今たまたま起こったとは考えにくいとしてゼロ仮説を棄却
⑤有意確率が有意水準よりも大きければ,そんなこともあるだろうと考えて,ゼロ仮説も棄却しない
| 母平均の検定 |
|---|
| R script |
n3 <- 200; p3 <- .95
sample03 <- sample(data01$income, size=n3)
m3 <- mean(sample03); sd3 <- sd(sample03)
N <- nrow(data01); alpha <- qt(0.5+p3/2, df=n3-1)
fpc <- sqrt((N-n3)/(N-1)); se <- sd3/sqrt(n3)
m3; sd3; alpha
m3 + c(-1, 1)*alpha*fpc*se # 有限母集団修正項付きC.I.
# ゼロ仮説
H0 <- 470
# 検定統計量
t0 <- (m3 - H0)/(fpc*se); t0
# 両側有意確率(有意水準より小さければゼロ仮説棄却)
pH0 <- pt(-1*abs(t0), df=n3-1) +
pt(abs(t0), df=n3-1, lower.tail=F)
pH0
|
| R console |
 |