〔訂正〕刊行後に見つかった誤りの訂正

　こんな事を言うと無責任であるのは否定出来ませんが，著者が自分の能力を超えた内容を説明しようと無理している為に，少なからぬ間違いが刊行後に指摘される事が予想されます。確認出来た誤りを，このページで纏めて訂正したいと思います。
　以下の様に目次に沿って訂正していく予定です。

準備　Rのインストールと操作の基本

第1章　1変量の記述統計の基礎

1　1変量についての要約統計量
1-2　代表値（中心傾向）
　003頁の以下の部分は，印刷されたテクストだと等号が一つに見えますが，ここは半角の等号が二つです。入稿した原稿では半角等号二つになっていますが印刷すると全角等号一つにしか見えないので訂正しておきます〔歸山亜紀さん（群馬県立女子大学）に教えて戴きました。2017.05.29〕。第1章1-2 代表値（中心傾向; central tendency）のスクリプトを御参照下さい。


第2章　2変数の関連の記述統計

2　分割表（クロス表）
2-3　名義尺度の連関係数
　026頁でファイ係数が最大値と最小値を取る場合について，数値（もしくは条件）があべこべになってしまっていました〔立教大学での授業中に気付きました。2018.05.24〕。


第4章　統計的検定の一般型

2　統計的検定における過誤
2-1　2種類の過誤と検定力
　060頁で誤字が有りました。〔上智大学受講生の方に御指摘戴きました。2018.06.11〕。


姉妹本『入門・社会調査法』の間違いの訂正

轟亮・杉野勇(編), [2010]2017, 『入門・社会調査法――2ステップで基礎から学ぶ〔第3版〕』, 京都: 法律文化社.
　上記の本の，杉野執筆章に間違いを見つけたので，ここでお詫びして訂正します。
第3版3刷までの間違い(現行版印刷書籍で未修正)
　第7章の発展「2 系統抽出の実際」表7-3(p. 110)にて，抽出番号の最初の数値89,595が千代田区の列に記載されていますが，連番始点と連番終点をよく見れば分かる通り，これは下の中央区に記載すべきです。第3版にする時に表全体を差し替えたのですが，その時に記載する列を誤った様です。申し訳ありませんでした。次の重版がもしあれば修正致します。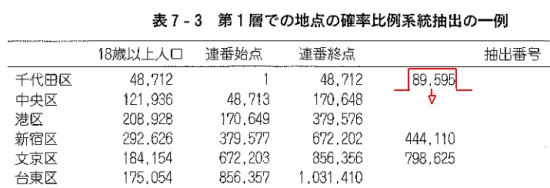


第3版初刷の間違い(2017.Sep.16. 2017年12月の第3版第2刷以降は修正済み)
　第11章の発展3「分散にも標本抽出分布がある」のp. 177にて，「不偏分散というものが母分散を中心とした正規分布をなすことがわかっている。」と書いていますが，これは間違いです。講義資料などではこうは書いていなかったのですが，うっかりミスをこれまで見逃してしまっていました。

　標本分散や不偏分散も，標本が変われば値が変わる標本統計量であり，標本抽出分布（sampling distribution; 一般には標本分布と呼ばれる）が存在する。しかし分散の標本抽出分布は正規分布ではない。『入門・社会統計学』のサポートウェブ第3章1-2で使用した4,894人分の模擬年収データを利用して示してみよう。
　分散の標本抽出分布がどんな形になるのかを検索して調べてみると，カイ二乗分布（を変換した分布）になる事がすぐに分かる。しかしこれは実はその変数の母集団分布が正規分布である場合の話であり，模擬年収データの様に正規分布ではない場合にどうなるのかは明らかではない。

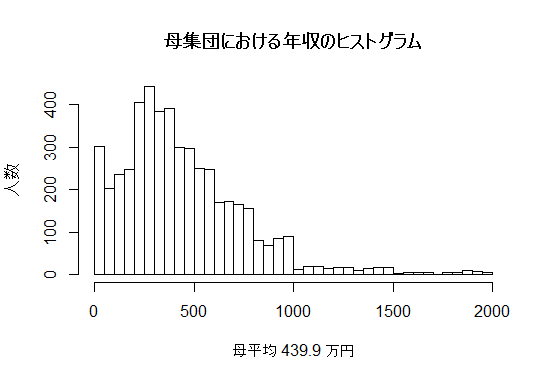
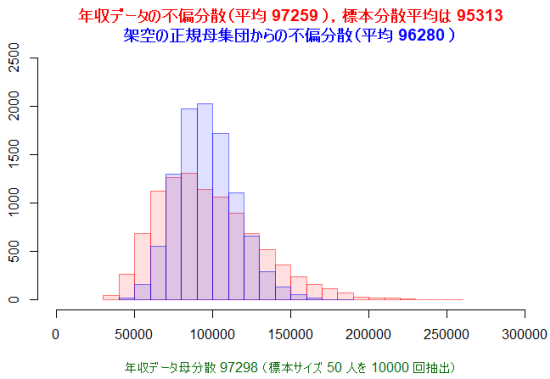
　このN=4894の母集団からサイズn=50の標本を抽出して不偏分散を計算すると云う作業を10000回繰り返し，得られた不偏分散をヒストグラムにしたものが，下の図の赤のグラフである。明らかに左右対称ではないので正規分布ではない。但しその10000個の不偏分散の平均は母分散にかなり近く，標本分散の平均よりも近い。ここから，母分散の近似値としては標本分散よりも不偏分散の方が良さそうである事が推察される。
　この図の青のグラフは，このN=4894の母集団と同じ平均，同じ標準偏差を有する正規母集団からn=50の標本を抽出して不偏分散を計算すると云う作業を10000回繰り返した結果である。母集団が正規分布であるか否かによって，不偏分散の標本抽出分布の形がかなり変わる事が分かる。

　この青のグラフは正規分布にも見えそうだが，これは正確にはカイ二乗分布を変換したものである。正規母集団から抽出された標本の不偏分散を，サンプルサイズと母分散を用いて変換した統計量の標本抽出分布がカイ二乗分布となる。以下の図が，その変換結果のグラフである。対応するカイ二乗分布を濃い緑で示した。
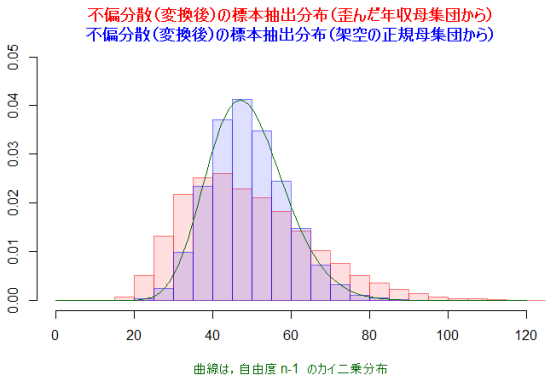
　この様に，実際のデータの不偏分散の標本抽出分布は，母集団分布が正規分布ではないと，理論的なカイ二乗分布とはかなり乖離する事が分かる。「正規母集団からの無作為標本の不偏分散（を変換した統計量）は，自由度n-1のカイ二乗分布に従う」と云う性質は，母集団分布が正規分布ではない場合には余り頑健(robust)とは言えない様である。