ピアソンの積率相関係数(correlation coefficient)
母相関係数のt検定(ゼロ仮説有意性検定)
『入門・社会統計学』演習用データ・ファイル:ダウンロード
| 標本相関と検定 |
|---|
| R script |
|---|
data01 <- read.csv("practice.csv")
names(data01)
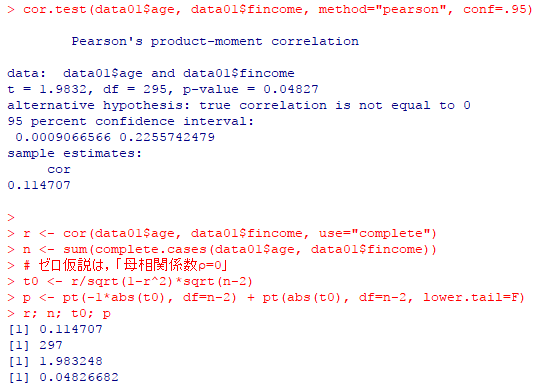
cor.test(data01$age, data01$fincome, method="pearson", conf=.95)
r <- cor(data01$age, data01$fincome, use="complete")
n <- sum(complete.cases(data01$age, data01$fincome))
# ゼロ仮説は,「母相関係数ρ=0」
t0 <- r/sqrt(1-r^2)*sqrt(n-2)
p <- pt(-1*abs(t0), df=n-2) + pt(abs(t0), df=n-2, lower.tail=F)
r; n; t0; p
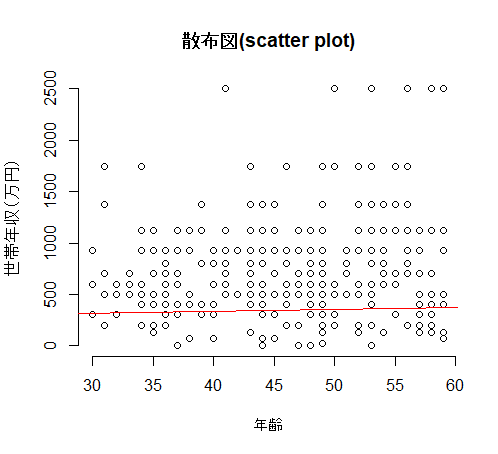
plot(data01$age, data01$fincome, bty="n",
main="散布図(scatter plot)", xlab="年齢", ylab="世帯年収(万円)")
abline(lm(income ~ age, data=data01), col="red") |
| R console |
|---|
 |
| R Graphics |
|---|
 |
母相関係数の区間推定
| 母相関係数の区間推定 |
|---|
| R script |
|---|
cor01 <- cor.test(data01$age, data01$fincome, method="pearson", conf=.95)
n <- sum(complete.cases(data01$age, data01$fincome))
names(cor01)
n; cor01$parameter
r <- cor01$estimate; r
cor01$conf.int
## 95%信頼区間を手計算
lwr <- 1/2*log((1+r)/(1-r))-qnorm(.975, 0, 1)/sqrt(n-3) # Lの信頼区間下限
upr <- 1/2*log((1+r)/(1-r))+qnorm(.975, 0, 1)/sqrt(n-3) # Lの信頼区間上限
# 逆変換して相関係数の値に戻す
rhoL <- (exp(2*lwr)-1)/(exp(2*lwr)+1)
rhoU <- (exp(2*upr)-1)/(exp(2*upr)+1)
rhoL; rhoU
|
| R console |
|---|
 |
積率相関と単回帰分析(simple regression analysis)
母相関係数の区間推定については,SRAの結果から単純に計算すると若干の誤差が生じる。
| SRAの回帰係数 |
|---|
| R script |
|---|
data01 <- read.csv("practice.csv")
names(data01)
data02 <- data01[complete.cases(data01$age, data01$fincome),]
cor2 <- cor.test(data02$age, data02$fincome)
reg1 <- lm(fincome ~ age, data=data02)
cor2
summary(reg1)
# 回帰係数から標本相関係数を算出(完全一致)
reg1$coefficient[2]*sd(data02$age)/sd(data02$fincome)
# 回帰係数の信頼区間から母相関係数の信頼区間を計算(若干の誤差)
confint(reg1, "age")*sd(data02$age)/sd(data02$fincome)
|
| R console |
|---|
 |
| SRAの標準化回帰係数 |
|---|
| R script |
|---|
cor2$conf.int # cor.test()の結果の再掲
sage <- scale(data02$age); sfincome <- scale(data02$fincome)
reg2 <- lm(sfincome ~ sage)
summary(reg2)
confint(reg2, "sage")
reg2$coefficient[2]^2 # 因みに,SRAの決定係数と相関係数の関係
|
| R console |
|---|
 |
| R script |
|---|
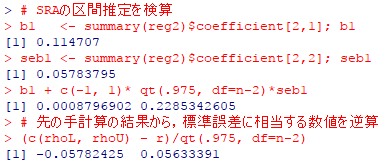
# SRAの区間推定を検算
b1 <- summary(reg2)$coefficient[2,1]; b1
seb1 <- summary(reg2)$coefficient[2,2]; seb1
b1 + c(-1, 1)* qt(.975, df=n-2)*seb1
# 先の手計算の結果から,標準誤差に相当する数値を逆算
(c(rhoL, rhoU) - r)/qt(.975, df=n-2)
|
| R console |
|---|
 |








