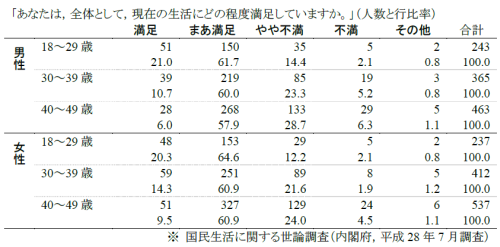
分割表(contingency table),クロス表(cross tabulation)
周辺分布(marginal distribution),比率
| xtabs()を使用した分割表とその拡充 |
|---|
| R script |
|---|
# 蔵書数q0200と最終学歴edu2
data01$books <- c(1:6)[data01$q0200]
t01 <- xtabs(~ edu2 + books, data=data01)
names(dimnames(t01)) <- list("最終学歴edu2", "蔵書数q0200")
dimnames(t01)[[1]] <- c("1 highschool", "2 college", "3 university")
dimnames(t01)[[2]] <- c("0-10", "11-25", "26-100", "101-200", "201-500", "500-")
t01 # 基本の表
addmargins(t01) # 周辺度数
# prop.table(t01, margin=1) # 行比率(出力は省略)
round(prop.table(t01, margin=1)*100, 1) # %で
# 分割表をそのままグラフ化するモザイクプロット
mosaicplot(t01, las=1, main="学歴別蔵書数",
col=rev(terrain.colors(6)))
|
| R console |
|---|
 |
| R Graphics |
|---|
 |
連関係数(coefficient of association)
まずは,2行×2列の分割表について,ユールのQ,φ係数,オッズ比を計算する。使用する変数は,四大卒以上かどうか(edu1),蔵書数が100冊以下か101冊以上か(books2)である。
| 2×2分割表に対するYule's Q,φ,odds ratio |
|---|
| R script |
|---|
# 大卒/非大卒(edu1)と蔵書数100冊以下か超か(books2)
data01$books2 <- c(1, 1, 1, 2, 2, 2)[data01$books]
t02 <- xtabs(~ edu1 + books2, data=data01)
t02
a <- t02[1,1]; b <- t02[1,2]; c <- t02[2,1]; d <- t02[2,2]
Q <- (a*d - b*c)/(a*d + b*c); Q
phi <- (a*d - b*c)/sqrt((a+b)*(c+d)*(a+c)*(b+d)); phi
odds_ratio <- (55/70)/(52/197); odds_ratio
|
| R console |
|---|
 |
| Harald Cramér's V |
|---|
| R script |
|---|
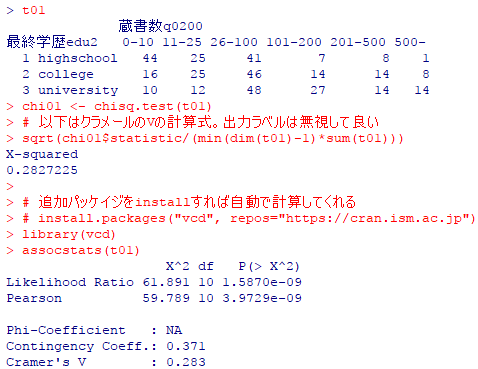
t01
chi01 <- chisq.test(t01)
# 以下はクラメールのVの計算式。出力ラベルは無視して良い
sqrt(chi01$statistic/(min(dim(t01)-1)*sum(t01)))
# 追加パッケイジをinstallすれば自動で計算してくれる
# install.packages("vcd", repos="https://cran.ism.ac.jp")
library(vcd)
assocstats(t01)
|
| R console |
|---|
 |
追加パッケイジのinstallは,PCにつき1回行えばよいが,Rをversion upするとパッケイジも通常は再installが必要になる。
library()による読み込みは,Rを起動する度に行う必要がある。一度読み込んだら,Rをquitするまでは有効である。
独立性のカイ二乗検定
| カイ二乗検定と残差分析 |
|---|
| R script |
|---|
t01
chi01 <- chisq.test(t01)
chi01
names(chi01)
round(chi01$expected, 1) # 期待度数
round(chi01$residuals, 2) # 標準化残差(ピアソン残差)
round(chi01$stdres, 2) # 調整済み標準化残差(ハーバーマン残差)
mosaicplot(t01, las=1, main="学歴別蔵書数", shade=T)
|
| R console |
|---|
 |
| R Graphics |
|---|
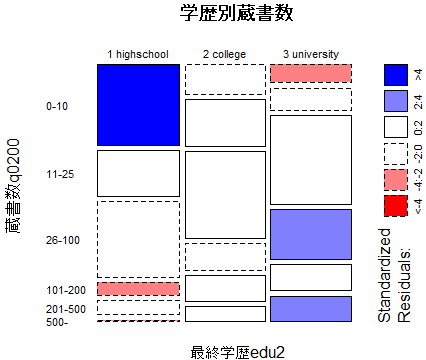 |
自由度kのカイ二乗分布は,独立したk個の標準正規変量の二乗和で定義される。この場合は,各セルの度数がポワソン分布で近似出来ると見做している。よって期待度数が5未満だと近似がうまくいかず,カイ二乗検定の条件を満たさないと考える事が多い。よくある基準は,期待度数が5未満のセルの数が全セル数の20%を超えてはいけないと云う基準,もしくは最小期待度数が1以上であると云う基準である。
カイ二乗検定が統計的に有意になった場合,「母集団でも恐らく独立ではないだろう」と判断するが,独立でない=何らかの関係があると言えるだけで,どの様な関係があるかは,カイ二乗検定だけからは分からない。また,統計的に有意になる事(有意確率の小ささ)と関連の強さは大標本においては別の事柄である点にも注意が必要。
三元分割表(三重クロス),順序連関係数
三元分割表(三重クロス)
| 行,列,層の三元分割表 |
|---|
| R script |
|---|
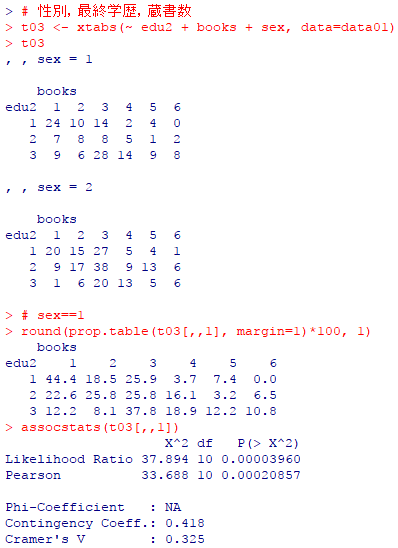
# 性別,最終学歴,蔵書数
t03 <- xtabs(~ edu2 + books + sex, data=data01)
t03
# sex==1
round(prop.table(t03[,,1], margin=1)*100, 1)
assocstats(t03[,,1])
# sex==2
round(prop.table(t03[,,2], margin=1)*100, 1)
assocstats(t03[,,2])
# そのまま表示させる場合の変数の並び順と,ftable()関数にあった並び順が異なる
ftable(xtabs(~ sex + edu2 + books, data=data01))
|
| R console |
|---|
 |
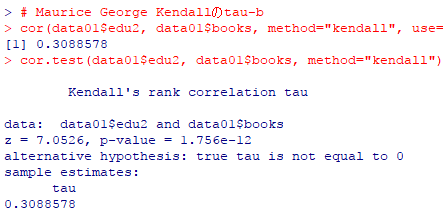
順序連関係数(rank correlation coefficient)
| 順序尺度同士の分割表 |
|---|
| R script |
|---|
# Maurice George Kendallのtau-b
cor(data01$edu2, data01$books, method="kendall", use="complete")
cor.test(data01$edu2, data01$books, method="kendall")
|
| R console |
|---|
 |
順序尺度同士の順序連関係数には,グッドマン=クラスカルのγ,ケンドールのτ(aからcの三種類)があるが,Rなどで簡単に計算出来るのはτbだけである。スピアマンの順位相関係数ρと云うものも一緒に紹介される事があるが,これは同順位が多い変数には適していない。