(対応の無い)2群の母平均の差の検定

スチューデントのt検定
統計的検定(NHST)であるからには必ず「ゼロ仮説」がある。その検定のゼロ仮説が何であるかを最初に確認する。
2群の平均値に差があるかどうかは,その平均値差が,そもそもその変数のバラつきに比べて大きいか小さいかが重要である。
詳しくは『入門・社会統計学』第6章1-2を参照。
| 男性と女性で幸福度の平均を比較 |
|---|
| R script |
# q1700=11は「わからない」で欠損値NAとすべきなので,新変数q1700bを作成。 data01$q1700b <- c(0:10)[data01$q1700+1] # 変数のリコード法には工夫 test1 <- t.test(data01$q1700b ~ data01$sex, var.equal=T) test1 # Student(William Sealy Gosset)のt検定 names(test1) diff(test1$estimate) # 平均値差 |
| R console |
 |
等分散性の検定
上述の様に,2群の母平均に差があるかどうかの検定は,標本平均の差が分散に比べて大きいか小さいかが重要。スチューデントのt検定は,2群における当該変数の分散が等しい事を前提にしている。なので,「等分散」であるかどうかを先に検討しなければならないとされてきた。
| 各群の母分散の等分散性の確認 |
|---|
| R script |
variances <- tapply(data01$q1700b, data01$sex, var, na.rm=T) variances var.test(data01$q1700b ~ data01$sex) variances[1]/variances[2] |
| R console |
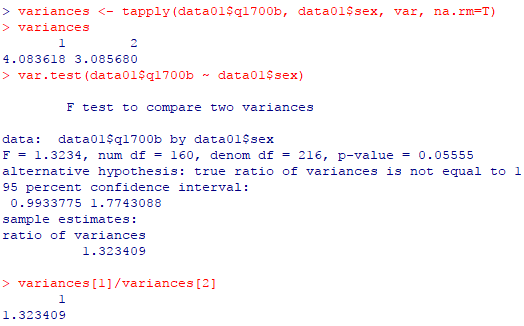 |
ゼロ仮説が棄却された場合は,「2群の母分散は(多分)等しいとは言えない」と云う結論になるが,棄却されなかった場合に「2群の母分散は(多分)等しい」と見做して良いかどうか――等分散であると言って良いかどうか――については論争がある。特に(ゼロ仮説有意性検定に批判的な見方が強まっている)最近は,「2群の母分散は等しい」事を意味しないとする立場が強い様に感じられる。「2群の母分散が異なると主張するには証拠が不十分である」,つまり,ゼロ仮説は間違いだとは言い切れないだけで,正しい事が示された訳では無いと云う解釈である。
ウェルチのt検定
男性と女性で教育年数(変数名edu)の平均に差があるかどうかを検定してみよう。
| 教育年数の男女差 |
|---|
| R script |
tapply(data01$edu, data01$sex, mean, na.rm=T)
tapply(data01$edu, data01$sex, var, na.rm=T)
var.test(data01$edu ~ data01$sex)
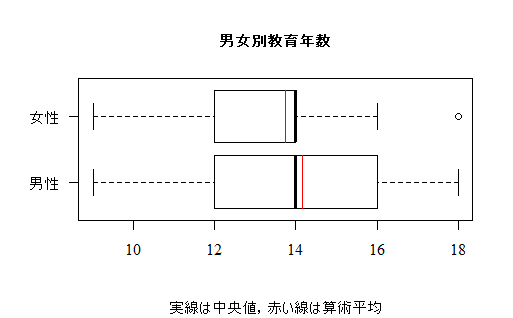
boxplot(data01$edu ~ data01$sex, las=1, cex.main=1,
main="男女別教育年数", sub="実線は中央値,赤い線は算術平均",
names=c("男性","女性"), horizontal=T)
m0 <- by(data01$edu, data01$sex, mean, na.rm=T)
segments(m0[1], 0.6, m0[1], 1.4, col="red")
segments(m0[2], 1.6, m0[2], 2.4, col="red")
|
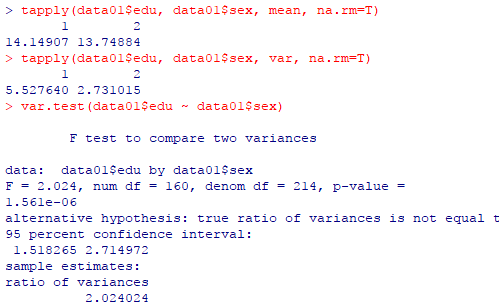
| R console |
 |
| R Graphics |
 |
等分散性が棄却されているので,等分散正規性を仮定するスチューデントのt検定は使えない事になる(分散比が3以内なら構わないとする考えもあり,その基準からすればこの場合もOKだが)。
教科書的に言えば,不等分散の場合は,ウェルチのt検定を使う事になっている(ウェルチ検定は等分散は仮定しないが,正規性は仮定している。)。
| ウェルチ検定 |
|---|
| R script |
test2 <- t.test(data01$edu ~ data01$sex, var.equal=F) test2 # Welch(Bernard Lewis Welch)のt検定 |
| R console |
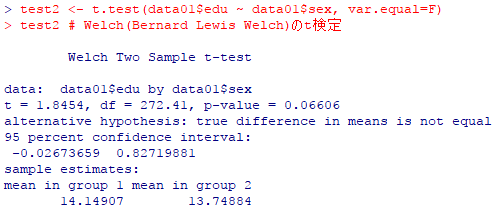 |
ウェルチの検定は,等分散の仮定を必要としない検定であり,等分散であると思われる時にも使用出来る。予め等分散か否かを検定して,等分散であればスチューデントを,不等分散であればウェルチを使うと云う昔の教科書の手順は「検定の多重性」の誤りを犯しており,現在では,最初からウェルチ検定だけを行うべきだと考える研究者が多い。Rのt.test()の関数も,var.equal=Tのオプションを指定しないとdefaultでウェルチ検定を行う仕様になっている。これは一要因分散分析のoneway.test()の関数も同じである。
スチューデントのt検定と一般線形モデル(General Linear Model)
スチューデントのt検定と一要因分散分析(oneway-ANOVA)
| 等分散の平均値差 |
|---|
| R script |
# Student(William Sealy Gosset)のt検定 test1 <- t.test(data01$q1700b ~ data01$sex, var.equal=T) test1 test1$statistic^2 # 検定統計量の対応 # oneway ANOVA oneway.test(data01$q1700b ~ data01$sex, var.equal=T) # Analysis Of Variance anova(aov(data01$q1700b ~ data01$sex)) |
| R console |
 |
ウェルチのt検定と一要因分散分析(oneway-ANOVA)
| 不等分散の平均値差 |
|---|
| R script |
# Welch(Bernard Leis Welch)のt検定 test2 <- t.test(data01$edu ~ data01$sex) test2 test2$statistic^2 # 検定統計量の対応 # oneway ANOVA oneway.test(data01$edu ~ data01$sex) |
| R console |
 |
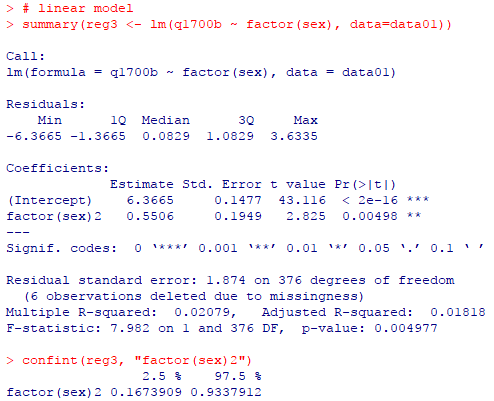
スチューデントのt検定と単回帰分析(Simple Regression Analysis)
| 線形モデル |
|---|
| R script |
test1 # Student's t-test diff(test1$estimate) # 標本平均値差 # linear model summary(reg3 <- lm(q1700b ~ factor(sex), data=data01)) confint(reg3, "factor(sex)2") |
| R console |
  |

