R introduction

重回帰分析(Multiple Regression Analysis)

モデルのF検定と分散説明率（決定係数）

幸福度を，年齢，教育年数，世帯年収で説明
R script
## 幸福度の欠損値処理（素朴な方法）
data01$q1700b <- data01$q1700
data01$q1700b[data01$q1700b == 11] <- NA

reg04 <- lm(q1700b ~ age + edu  + fincome, data=data01)
sum04 <- summary(reg04)
sum04
R console
モデルのF検定，分散説明率
R script
# residuals
summary(reg04$residuals)
mean(reg04$residuals)
quantile(reg04$residuals, probs=c(0, .05, .10, .25, .50, .75, .90, .95,  1))

# F value, p value
F0 <- (var(reg04$fitted.values)/3)/(var(reg04$residuals)/
(length(reg04$residuals)-3-1)); F0
(var(reg04$fitted.values)/(reg04$rank-1))/(var(reg04$residuals)/reg04$df.residual)
# 別の書き方
pf(F0, df1=3, df2=length(reg04$residuals)-3-1, lower.tail=F)
R console
R script
# R-square
1-var(reg04$residuals)/var(reg04$residuals + reg04$fitted.values)
1-var(reg04$residuals)/var(reg04$model$q1700b) # 別の書き方

# adjusted R-square
1-var(reg04$residuals)*length(reg04$residuals)/(length(reg04$residuals)-3-1)/
(var(reg04$residuals + reg04$fitted.values)*length(reg04$residuals)/
(length(reg04$residuals)-1))
1-var(reg04$residuals)/(length(reg04$residuals)-3-1)/(var(reg04$residuals +
 reg04$fitted.values)/(length(reg04$residuals)-1)) # 別の書き方

# 丁寧な書き方
SSr <- var(reg04$residuals)*length(reg04$residuals)
MSr <- SSr/reg04$df.residual
SSt <- var(reg04$model$q1700b)*length(reg04$model$q1700b)
MSt <- SSt/(length(reg04$model$q1700b)-1)
adj.R2 <- 1 - MSr/MSt; adj.R2
R console

偏回帰係数(partial regression coefficient)のt検定と区間推定

係数(coefficients)
R script
# coefficientsのt検定。出力と検算
coef <- summary(reg04)$coefficients; coef
coef[,1]/coef[,2]
pt(abs(coef[,1]/coef[,2]), df=reg04$df.residual, lower.tail=F)*2

# coefficientsの区間推定。出力と検算
confint(reg04)
coef[,1] + coef[,2] %o% (c(-1, 1) * qt(.975, df=reg04$df.residual))
coef[,1] + cbind(-1 * (a <- qt(.975, df=reg04$df.residual) * coef[,2]), a) # 別の書き方
R console

標準化偏回帰係数(standardized partial regression coefficient)

分析に使用するケースだけに限定してから標準化する
R script
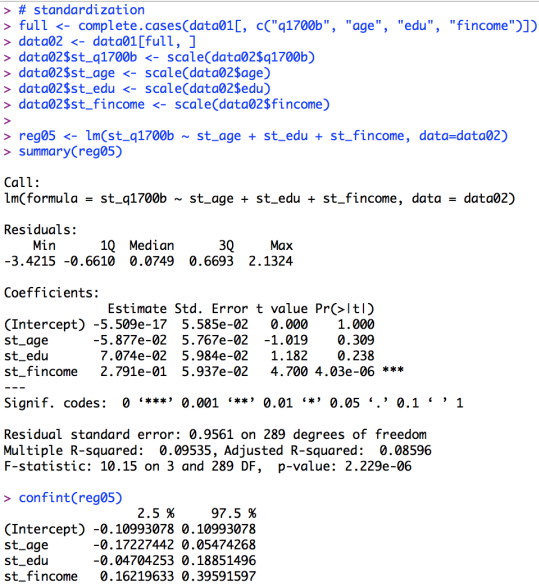
# standardization
full <- complete.cases(data01[, c("q1700b", "age", "edu", "fincome")])
data02 <- data01[full, ]
data02$st_q1700b <- scale(data02$q1700b)
data02$st_age <- scale(data02$age)
data02$st_edu <- scale(data02$edu)
data02$st_fincome <- scale(data02$fincome)

reg05 <- lm(st_q1700b ~ st_age + st_edu + st_fincome, data=data02)
summary(reg05)
confint(reg05)
R console

交互作用項(interaction term)など

要因（名義尺度），交互作用項，二乗項，多重共線性
R script
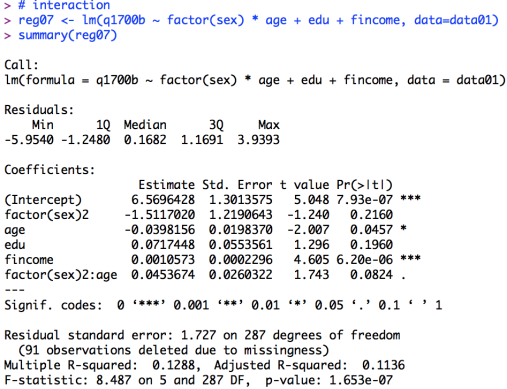
# nominal scale
reg06 <- lm(q1700b ~ factor(sex) + age + edu + fincome, data=data01)
sum06 <- summary(reg06)
sum06

# interaction
reg07 <- lm(q1700b ~ factor(sex) * age + edu + fincome, data=data01)
summary(reg07)

# interactions
reg07b <- lm(q1700b ~ factor(sex) * (age + edu)  + fincome, data=data01)
summary(reg07b)

# interaction only
reg07c <- lm(q1700b ~ factor(sex) : age + edu + fincome, data=data01)
summary(reg07c)
R console

R script
# squared term
reg08 <- lm(q1700b ~ factor(sex) + age + edu + fincome + I(fincome^2), data=data01)
sum08 <- summary(reg08)
sum08

# multiple colinearity
# install.packages("car", repos="https://cran.ism.ac.jp")
library(car)
vif(reg07) # Variance Inflation Factor
1/vif(reg07) # torelance
R console

一要因分散分析と重回帰分析w/ダミー変数

3水準以上の一要因分散分析と，複数のダミー変数を用いた重回帰分析は，数学的に同値であり，分散分析，回帰分析，共分散分析を全て含んで「一般線形モデル」と云う。要件は，従属変数（誤差）に等分散正規性を仮定する事である。

分散分析と重回帰分析の同値性
R script
# oneway-ANOVA and MRA with dummy variables
tapply(data01$q1700b, data01$edu2, mean, na.rm=T)
anova(aov01 <- aov(q1700b ~ factor(edu2), data=data01))
pairwise.t.test(data01$q1700b, data01$edu2, p.adj="hommel", pool.sd=F)
pairwise.t.test(data01$q1700b, data01$edu2, p.adj="none", pool.sd=T)

data01$d1 <- c(0, 1, 0)[data01$edu2]
data01$d2 <- c(0, 0, 1)[data01$edu2]
summary(lm01 <- lm(q1700b ~ d1 + d2, data=data01))

sum(summary(lm01)$coefficients[1:2, 1])
sum(summary(lm01)$coefficients[c(1,3), 1])
R console

（一般）線形モデルを分析する lm() 関数は，要因型変数を投入すれば，自動的に上記の様な dummy coding をしてくれるので，実際に上の様に自分でダミー変数を作成する必要は無い。また，要因型変数と変量型変数を同時投入する事も全く問題ない。共分散分析(ANCOVA; Analysis of Covariance)も要因型と変量型を同時投入するので形の上では同じだが，共分散分析の場合には変量型変数（＝共変量）には主たる関心は無く，要因型変数の効果を正確に測定する為に共変量が投入される。一般線形モデルの場合にはその様な非対称性は特に想定しなくて良い。

要因型変数を投入したlm()
R script
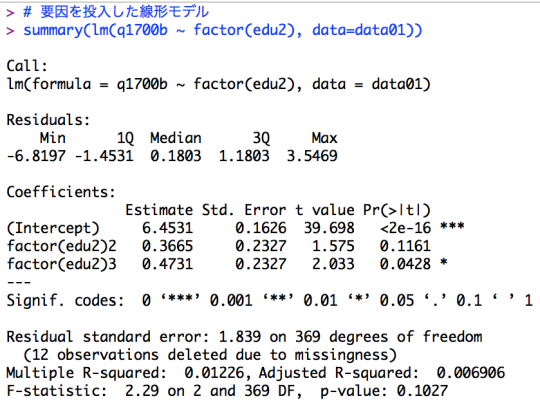
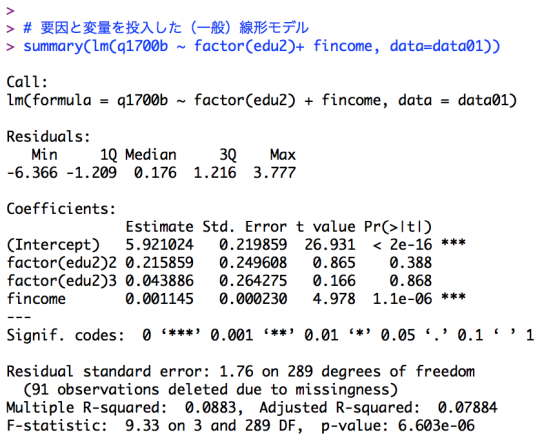
# 要因を投入した線形モデル
summary(lm(q1700b ~ factor(edu2), data=data01))

# 要因と変量を投入した（一般）線形モデル
summary(lm(q1700b ~ factor(edu2) + fincome, data=data01))
R console

古典的パス解析(classical path analysis)

sem()関数を使用した一例
R script
# path analysis
data03 <- data02[, c("age", "edu", "fincome", "q1700b")]
n1 <- nrow(data03) # SEMの為にケース数を保存
cor2 <- cor(data03) # SEMの為に相関係数行列を保存

# install.packages("sem", repos="https://cran.ism.ac.jp")
library(sem)
opt <- options(fit.indices = c("GFI", "AGFI", "RMSEA", "AIC", "BIC"))

pathE <- specifyEquations()
    edu = b12*age
    fincome = b13*age + b23*edu
    q1700b = b14*age + b24*edu + b34*fincome
    V(age) = v1
    V(edu) = v2
    V(fincome) = v3
    V(q1700b) = v4

resultE <- sem(pathE, cor2, N=n1, data=data03)
summary(resultE)

# 重回帰分析の組み合わせと比較
summary(lm(scale(edu) ~ scale(age), data=data03))
summary(lm(scale(fincome) ~ scale(age) + scale(edu), data=data03))
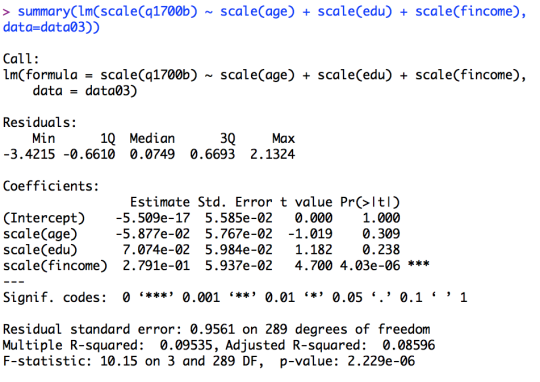
summary(lm(scale(q1700b) ~ scale(age) + scale(edu) + scale(fincome), data=data03))
R console


Graphviz(GVedit)で描いたパスダイアグラム

一般化線形モデル(Generalized Linear Model)

二項ロジスティック回帰モデル

従属変数が二値で，リンク関数を用いて最尤法で解く，一般"化"線形モデルの一つ
R script
# binary logistic regression. edu1は大卒か非大卒か
result <- glm(edu1 ~ factor(sex) + age + I(age^2), family = binomial(link =
 "logit"), data=data01)
summary(result)

# install.packages("ResourceSelection", repos="https://cran.ism.ac.jp")
library(ResourceSelection)
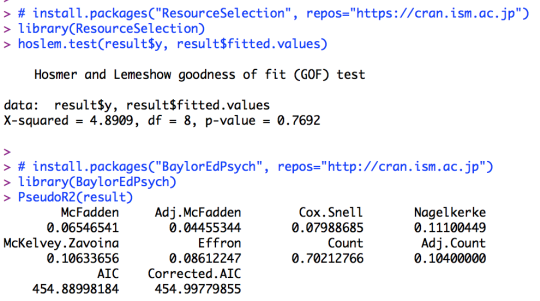
hoslem.test(result$y, result$fitted.values)

# install.packages("BaylorEdPsych", repos="http://cran.ism.ac.jp")
library(BaylorEdPsych)
PseudoR2(result)
R console

R logo

↑ PAGE TOP