杉野 勇 (SUGINO Isamu) お茶の水女子大学・人間発達科学専攻・応用社会学コース担当
『入門・社会統計学』サポートウェブ |
|
1 ベイズ統計学の初歩的な考え方
本文では,これまでの頻度主義統計学(frequentist statistics)もしくはゼロ仮説有意性検定(NHSTP)に対する批判が近年強まっており,その代りにベイズ統計学(Bayesian statistics)への注目が強まっている事に少しだけ触れた。ここでは,ベイズ統計学もしくはベイズ主義の考え方のごく初歩だけを解説する。ベイズ統計学は,計量・統計分析のオルタナティヴとして勢力を増しているだけではなく,定性的(質的)研究(Qualitative Analysis)においても関心が高まっていると言える。

1-1 客観確率と主観確率,事前確率と事後確率
頻度主義においては,「確率」とは,認識する主体とは無関係に,世界に事実として存在する性質を意味している。これを「客観確率」と呼んでおく。サイコロを振った時に1の目が出る確率が1/6であるというのは,誰がそれについて考えるかとは関係のない数字であると想定されている。実際に,或具体的なサイコロで1の目が出る確率が本当に1/6であるかどうかは,原理的には確認するのは難しい。サイコロが綿密に製造されていれば,たくさんの回数そのサイコロを振っていればおおよそ1/6で安定していく事が期待されるが,無限にそのサイコロを振り続けて1の目が出る確率を記録して行っても,厳密に1/6であり続ける保証はなく,ほんの僅か歪んでいる可能性が否定出来ないかも知れない。そもそもそのような無限の試行は実際には困難であるし,振っている間に摩耗して正確なサイコロで無くなっていくかもしれない。
これに対して「主観確率」は,主体・行為者が思念の中で付与する確率である。「私はこのサイコロで1の目が出る確率は1/6だと思う/信じる」と云うのは主観確率である。「この授業で単位が取れる確率は五分五分だな」と云うのも主観確率である。世界が事実として有する性質であると想定されている客観確率は,(その確率を考える事象が時間的・空間的・物理的に同一であれば)変化しない筈であるが,同一の事象についての主観確率は簡単に変化するし,人によって値が全く異なり得る。その事に何も不合理性はない。「確率評価が変化する」と云う言い方をしても良いだろう。
ベイズ統計学は上の主観確率を対象としていると考えられる事もあるが,必ずしも主観的であると云う部分,或は個人差を強調する必要はない。重要なのは,主体・行為者によって異なるかどうかと云う事ではなく,確率評価が(理由を持って)変化すると云う事である。例えば,以前は或要因間関連が存在する確率を10%と見積もっていたが,何らかのデータ・情報・証拠が手に入った事によりその認識が改められ,その関連の存在に対する確率評価が40%と変化する,と云うのがベイズ原理の基本的な考え方である。「事前確率が,データによって更新されて,事後確率に変化する」と表現出来るだろう。
これに対して「主観確率」は,主体・行為者が思念の中で付与する確率である。「私はこのサイコロで1の目が出る確率は1/6だと思う/信じる」と云うのは主観確率である。「この授業で単位が取れる確率は五分五分だな」と云うのも主観確率である。世界が事実として有する性質であると想定されている客観確率は,(その確率を考える事象が時間的・空間的・物理的に同一であれば)変化しない筈であるが,同一の事象についての主観確率は簡単に変化するし,人によって値が全く異なり得る。その事に何も不合理性はない。「確率評価が変化する」と云う言い方をしても良いだろう。
ベイズ統計学は上の主観確率を対象としていると考えられる事もあるが,必ずしも主観的であると云う部分,或は個人差を強調する必要はない。重要なのは,主体・行為者によって異なるかどうかと云う事ではなく,確率評価が(理由を持って)変化すると云う事である。例えば,以前は或要因間関連が存在する確率を10%と見積もっていたが,何らかのデータ・情報・証拠が手に入った事によりその認識が改められ,その関連の存在に対する確率評価が40%と変化する,と云うのがベイズ原理の基本的な考え方である。「事前確率が,データによって更新されて,事後確率に変化する」と表現出来るだろう。
1-2 証拠・データによる確率評価の更新(update)
データ・情報によって確率が更新される例を幾つか考えてみよう。
よくある例は,病気の検査の例である。或病気に罹患する確率が10%(.10)だとしよう。その病気の検査は,90%の確率で正しく識別するとする。言い換えれば,罹患していない人に対して陽性反応を出す偽陽性の確率が10%,罹患している人に対して陰性反応を出す偽陰性の確率も10%である(偽陽性と偽陰性の確率は必ずしも等しいとは限らない)。この時,検査で陽性となった人が,その病気に罹患している確率はどれくらいだろうか?
一般にはこの問いに対して,検査の精度である90%に近い確率を答える人が多い。しかしベイズの考え方では,(何の情報も無い状態での)事前確率は,一般的な罹患率を考える。つまり,その人が罹患している事前確率は10%である。一方,検査で陽性が出る人は,罹患していて検査で正しく検出される人と,罹患していないのに偽陽性が出る人の二種類がいる。検査で陽性が出たと云う事は,少なくともこの二つのグループのうちのどちらかに属する事は確かなので,「検査で陽性が出た時に,実際に病気に罹患している確率」は,この二つのグループのうち前者に含まれる確率,となる。
1000人の人がいた時に,罹患者は100人,そうでない人は900人と考えられる。これが全員この検査を受けたとすると,正しく陽性反応が出るのが100人×.90=90人,偽陽性が900人×.10=90人,合計で180人である。この180人に含まれる人が,実際に罹患している確率は,90/180=50%と云う事になる。事前確率が小さい場合(事前分布で比率がかなり少ない場合),事後確率は事前確率の10%よりは大幅に高くなるが,それでもまだ検査の精度90%に比べるとかなり低い値にとどまる。
事前確率と検査の精度を与えると,更新された事後確率を出力するRスクリプトが以下である。色々な数値を設定して結果を確認してみよう。下の実行結果では上と少し異なる数値で例示している。

科学的知識もこうした確率の更新(信念の更改)と同じ形式で考える事が出来る。
或因果説明が正しいと云う事前確率が,その後得られた証拠に照らして更新され,事後確率が高まる(低まる),と考える。
例えば,最初,因果関係についての理論仮説Aが正しいかどうかの確率は半々であるとする(事前確率.50)。
次に,その仮説Aが正しい時に,或事象bが観察される確率が,.75であるとする。
その仮説Aが正しくない時に,同じその事象bが観察される確率が,.25であるとする。
もし,定性的調査の結果,その事象bが観察されたとすると,仮説Aが正しい確率はどうなるであろうか。

理論(または理論的説明)の尤もらしさが,(その理論の観察可能な含意についての)観察結果により,事前確率から事後確率に変化するのである。

以下の例のそれぞれがどの様な研究の成果を意味しているのか考えてみよう。


よくある例は,病気の検査の例である。或病気に罹患する確率が10%(.10)だとしよう。その病気の検査は,90%の確率で正しく識別するとする。言い換えれば,罹患していない人に対して陽性反応を出す偽陽性の確率が10%,罹患している人に対して陰性反応を出す偽陰性の確率も10%である(偽陽性と偽陰性の確率は必ずしも等しいとは限らない)。この時,検査で陽性となった人が,その病気に罹患している確率はどれくらいだろうか?
一般にはこの問いに対して,検査の精度である90%に近い確率を答える人が多い。しかしベイズの考え方では,(何の情報も無い状態での)事前確率は,一般的な罹患率を考える。つまり,その人が罹患している事前確率は10%である。一方,検査で陽性が出る人は,罹患していて検査で正しく検出される人と,罹患していないのに偽陽性が出る人の二種類がいる。検査で陽性が出たと云う事は,少なくともこの二つのグループのうちのどちらかに属する事は確かなので,「検査で陽性が出た時に,実際に病気に罹患している確率」は,この二つのグループのうち前者に含まれる確率,となる。
1000人の人がいた時に,罹患者は100人,そうでない人は900人と考えられる。これが全員この検査を受けたとすると,正しく陽性反応が出るのが100人×.90=90人,偽陽性が900人×.10=90人,合計で180人である。この180人に含まれる人が,実際に罹患している確率は,90/180=50%と云う事になる。事前確率が小さい場合(事前分布で比率がかなり少ない場合),事後確率は事前確率の10%よりは大幅に高くなるが,それでもまだ検査の精度90%に比べるとかなり低い値にとどまる。
事前確率と検査の精度を与えると,更新された事後確率を出力するRスクリプトが以下である。色々な数値を設定して結果を確認してみよう。下の実行結果では上と少し異なる数値で例示している。
prior <- .05 # 有徴である事前確率
correct.p <- .95 # 有徴のケースで検査が正しく陽性になる確率
correct.n <- .85 # 無徴のケースで検査が正しく陰性になる確率
# 検査で陽性が出た場合に,確かに有徴である事後確率
posterior <- prior * correct.p / (prior * correct.p + (1-prior) * (1-correct.n))
## 詳しい例示
n <- 1000 # 仮に何人の人がいたと仮定するか
text1 <- sprintf("事前確率(%.1f%%): 有徴者%.1f人,無徴者%.1f人", prior*100, n*prior, n*(1-prior))
text2 <- sprintf("有徴者の検査結果: 陽性%.1f人,偽陰性%.1f人", p1 <- n*prior*correct.p, n*prior*(1-correct.p))
text3 <- sprintf("無徴者の検査結果: 偽陽性%.1f人,陰性%.1f人", p2 <- n*(1-prior)*(1-correct.n), n*(1-prior)*correct.n)
text4 <- sprintf("陽性のうち有徴者(事後確率): %.1f人中%.1f%%", p1 + p2, p1/(p1+p2)*100)
text1; text2; text3; text4
correct.p <- .95 # 有徴のケースで検査が正しく陽性になる確率
correct.n <- .85 # 無徴のケースで検査が正しく陰性になる確率
# 検査で陽性が出た場合に,確かに有徴である事後確率
posterior <- prior * correct.p / (prior * correct.p + (1-prior) * (1-correct.n))
## 詳しい例示
n <- 1000 # 仮に何人の人がいたと仮定するか
text1 <- sprintf("事前確率(%.1f%%): 有徴者%.1f人,無徴者%.1f人", prior*100, n*prior, n*(1-prior))
text2 <- sprintf("有徴者の検査結果: 陽性%.1f人,偽陰性%.1f人", p1 <- n*prior*correct.p, n*prior*(1-correct.p))
text3 <- sprintf("無徴者の検査結果: 偽陽性%.1f人,陰性%.1f人", p2 <- n*(1-prior)*(1-correct.n), n*(1-prior)*correct.n)
text4 <- sprintf("陽性のうち有徴者(事後確率): %.1f人中%.1f%%", p1 + p2, p1/(p1+p2)*100)
text1; text2; text3; text4

科学的知識もこうした確率の更新(信念の更改)と同じ形式で考える事が出来る。
或因果説明が正しいと云う事前確率が,その後得られた証拠に照らして更新され,事後確率が高まる(低まる),と考える。
例えば,最初,因果関係についての理論仮説Aが正しいかどうかの確率は半々であるとする(事前確率.50)。
次に,その仮説Aが正しい時に,或事象bが観察される確率が,.75であるとする。
その仮説Aが正しくない時に,同じその事象bが観察される確率が,.25であるとする。
もし,定性的調査の結果,その事象bが観察されたとすると,仮説Aが正しい確率はどうなるであろうか。
prior <- .50; names(prior) <- c("仮説Aが正しい事前確率")
b.A <- .75; names(b.A) <- c("Aが正しい時に事象bが観察される確率")
b.notA <- .25; names(b.notA) <- c("Aが正しくない時にbが観察される確率")
posterior <- prior * b.A / (prior * b.A + (1-prior) * b.notA)
names(posterior) <- c("bが観察された時に,Aが正しい事後確率")
prior; b.A; b.notA; posterior
b.A <- .75; names(b.A) <- c("Aが正しい時に事象bが観察される確率")
b.notA <- .25; names(b.notA) <- c("Aが正しくない時にbが観察される確率")
posterior <- prior * b.A / (prior * b.A + (1-prior) * b.notA)
names(posterior) <- c("bが観察された時に,Aが正しい事後確率")
prior; b.A; b.notA; posterior

理論(または理論的説明)の尤もらしさが,(その理論の観察可能な含意についての)観察結果により,事前確率から事後確率に変化するのである。

以下の例のそれぞれがどの様な研究の成果を意味しているのか考えてみよう。


2 頻度論(frequentist)的推定・検定とベイズ統計学
以下では,ここまで頻度論的(頻度主義的)統計学に基づいて説明して来た統計的検定・推定を,ベイズ統計学(ベイジアン統計学)で解くとどうなるかを簡単に例示してみる。今後,Rでベイズ統計学的分析を行う環境としては,RStanが拡大していくと予想するが,RStanを使用可能にするには,rstanパッケイジ以外に,C++コンパイラなどをインストールする必要があったり, RStudioの様なサポートアプリケイションのインストールが強く推奨されたりするので,本書が想定している初学者や本書で学んだ初級者には難易度が高いと思われる。従ってここでは,本書でおおよそRを学習したユーザなら簡単に導入出来る"MCMCpack"パッケイジで例示を行っていく。MCMCpackもこれまではRでベイズ統計的分析を行うのに広く使われてきたものである。
2-1 2群の母平均の差のt検定――ベイズ統計学の基礎の例示
ここで詳しく説明するのはとても無理なので,詳細は専門の書籍やウェブサイトを参照して貰う事として,最低限の知識だけを例示していくにとどめる。
MCMCpackのインストール
ステューデントのt検定と二値変数による単回帰分析の確認
次に,第6章1-2の2群の母平均の差のステューデントt検定を改めて実行しておく。

ステューデントのt検定と二値変数による単回帰分析は完全に一致する事をもう一度確認しておこう。
MCMC; Markov Chain Monte Carlo法
ここからがベイズ統計学の概略。大胆に簡略化して説明すると,
① 求めたい母数の値について,出来るだけ条件を置かない事前確率分布を指定する(一様分布や,極めて分散の大きな正規分布など)。つまり,とても広範囲の様々な値を,ほぼ同じ様な(小さな)確率で取り得ると仮定する。
② 調査で得られたデータから,様々な母数の尤度を求める。
③ ベイズの原理に従って,事前確率×尤度=事後確率が最大になる母数を求める。
実際には,この事後確率の分布,事後確率分布を求めるのは極めて大変なので,乱数を活用したシミュレイションによって事後分布を求める方法が,コンピュータの性能の劇的な向上と共に一般化した。その代表的なものが,マルコフ連鎖モンテカルロ(MCMC)法と呼ばれる方法である。
MCMCでは,乱数から出発してランダムに変動する一繋がりの(しばしば膨大な数の)推定値群を得る。初期値に用いた乱数の影響が及ぶので最初の方の推定値群は母数の推定値としては好ましくないが,十分な回数の変化を経た後は,母数の推定値として使用出来ると考えられる。そうした推定値が膨大な数だけ集まれば,それを母数の事後確率分布と見做す事が出来る。
初期値の影響が残っているかどうかを確認する為に,初期値を変えて乱数の系列生成を行い,最終的に似た様な事後分布になるかどうか(収束するかどうか)を確認する。
ここまでを,上の幸福度と性別の例で試してみよう。使用する関数は,MCMCregress( )である。burnin=は,最初の何個の数字を捨てるか,mcmc=はその系列で推定値を何個発生させるか,thin=は何個おきに推定値を残すか,seed=は乱数の種の指定である。
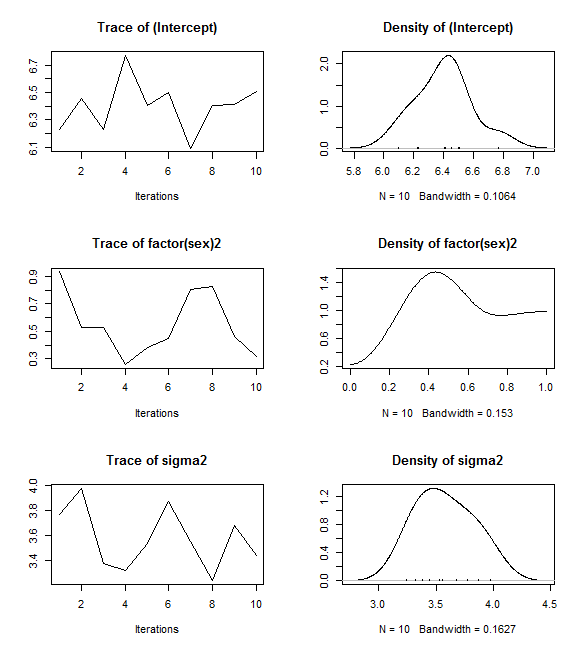
これは推定値を10個(繰り返しの数 mcmc=10)しか生成しておらず,連鎖(chain)は出たらめに上下し,ヒストグラムの形も滑らかではない。通常は,繰り返しの数はもっと遥かに大きな値を指定する。以下では,mcmc=100, mcmc=1000, mcmc=10000として,グラフがどの様になっていくかを示してみよう(スクリプトは省略,グラフも真ん中の factor(sex)2 のもののみ)。
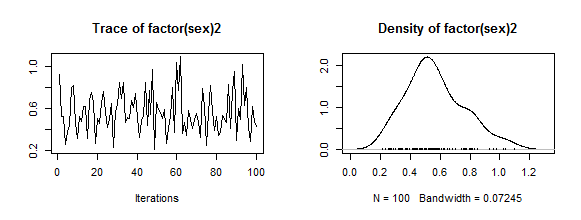
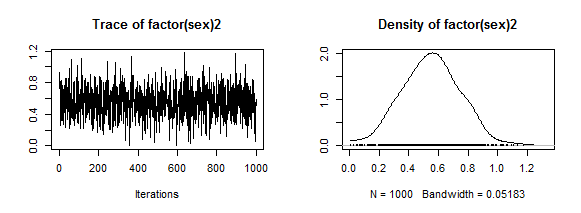
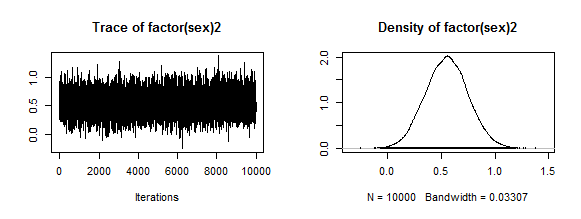
以下では,burnin=1000として最初の1000個の数字は捨ててmcmc=100000としてそれぞれ100000個の数字からなる異なる系列を3つ生成した上で10個おきの数字だけを採用し(thin=10,3系列を1つに纏めた上で図示し,且つ summary( )で計算結果の数字を確認しよう。また,収束しているか否か(きちんとした信頼できる結果が得られているか否か)を診断する関数も付記だけしておく(収束診断の結果は省略)。
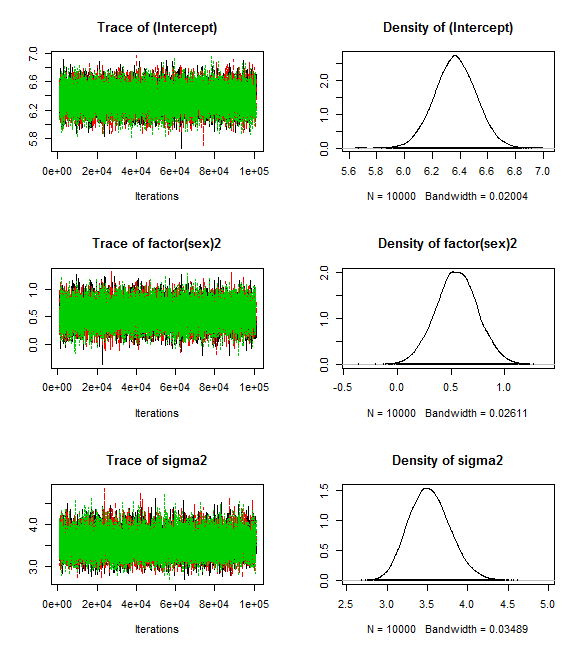

切片(Intercept),男性に対する女性の平均差(factor(sex)2),誤差分散(sigma2)のそれぞれについて,10000個の推定値が3系列あるので全部で30000個の推定値が得られ,その事後分布の平均(Mean)や標準偏差(SD),2.5%点や97.5%点が表示されている。
2.5%点から97.5%点の範囲は,頻度主義ではconfidence interval(信頼区間)と呼ぶが,ベイズ統計学においては,credible interval(信用区間或は確信区間)と呼ばれている。ベイズのcredible intervalの解釈は非常に素朴で分かり易く,「母数がその区間に存在する確率が95%である。」と云ったものになる。
この結果を,上のステューデントのt検定または単回帰分析の結果と比較してみると,新しい統計学を導入した割には,結果は殆ど一致しているので拍子抜けするかも知れない。実は,初歩的な重回帰分析くらいでは頻度主義の95%信頼区間とベイズの95%確信区間はほぼ変わらない事が多い。ベイズ統計学を本当に活用する為には,もっと複雑なモデル,前提を置かないモデルなどで柔軟な分析をするのが良いかも知れない。
MCMCpackのインストール
install.packages("MCMCpack", repos="https://cran.ism.ac.jp", dependencies=T)
library(MCMCpack)
もし,library(MCMCpack)のところで他に足りないパッケイジがあると云った警告が出てうまく読み込まれなければ,install.packages()関数にそのパッケイジ名を指定して追加インストールして下さい。library(MCMCpack)
ステューデントのt検定と二値変数による単回帰分析の確認
次に,第6章1-2の2群の母平均の差のステューデントt検定を改めて実行しておく。
data01 <- read.csv("practice.csv")
names(data01)
# 幸福度q1700の処理
data01$q1700b <- c(0:10)[data01$q1700+1] # recode方法に若干の工夫
t01 <- t.test(data01$q1700b ~ data01$sex, var.equal=T) # Studentのt検定
r01 <- lm(q1700b ~ factor(sex), data01) # 同じ分析を単回帰分析(SRA)で実行
t01 # Student's t-testの結果
summary(r01); confint(r01) # SRAの検定と区間推定
names(data01)
# 幸福度q1700の処理
data01$q1700b <- c(0:10)[data01$q1700+1] # recode方法に若干の工夫
t01 <- t.test(data01$q1700b ~ data01$sex, var.equal=T) # Studentのt検定
r01 <- lm(q1700b ~ factor(sex), data01) # 同じ分析を単回帰分析(SRA)で実行
t01 # Student's t-testの結果
summary(r01); confint(r01) # SRAの検定と区間推定

ステューデントのt検定と二値変数による単回帰分析は完全に一致する事をもう一度確認しておこう。
MCMC; Markov Chain Monte Carlo法
ここからがベイズ統計学の概略。大胆に簡略化して説明すると,
① 求めたい母数の値について,出来るだけ条件を置かない事前確率分布を指定する(一様分布や,極めて分散の大きな正規分布など)。つまり,とても広範囲の様々な値を,ほぼ同じ様な(小さな)確率で取り得ると仮定する。
② 調査で得られたデータから,様々な母数の尤度を求める。
③ ベイズの原理に従って,事前確率×尤度=事後確率が最大になる母数を求める。
実際には,この事後確率の分布,事後確率分布を求めるのは極めて大変なので,乱数を活用したシミュレイションによって事後分布を求める方法が,コンピュータの性能の劇的な向上と共に一般化した。その代表的なものが,マルコフ連鎖モンテカルロ(MCMC)法と呼ばれる方法である。
MCMCでは,乱数から出発してランダムに変動する一繋がりの(しばしば膨大な数の)推定値群を得る。初期値に用いた乱数の影響が及ぶので最初の方の推定値群は母数の推定値としては好ましくないが,十分な回数の変化を経た後は,母数の推定値として使用出来ると考えられる。そうした推定値が膨大な数だけ集まれば,それを母数の事後確率分布と見做す事が出来る。
初期値の影響が残っているかどうかを確認する為に,初期値を変えて乱数の系列生成を行い,最終的に似た様な事後分布になるかどうか(収束するかどうか)を確認する。
ここまでを,上の幸福度と性別の例で試してみよう。使用する関数は,MCMCregress( )である。burnin=は,最初の何個の数字を捨てるか,mcmc=はその系列で推定値を何個発生させるか,thin=は何個おきに推定値を残すか,seed=は乱数の種の指定である。
b1 <- MCMCregress(q1700b ~ factor(sex), data=data01,
burnin=0, mcmc=10, thin=1, seed=1234)
plot(b1) # 左に発生した推定値の系列,右にその分布のヒストグラム
burnin=0, mcmc=10, thin=1, seed=1234)
plot(b1) # 左に発生した推定値の系列,右にその分布のヒストグラム

これは推定値を10個(繰り返しの数 mcmc=10)しか生成しておらず,連鎖(chain)は出たらめに上下し,ヒストグラムの形も滑らかではない。通常は,繰り返しの数はもっと遥かに大きな値を指定する。以下では,mcmc=100, mcmc=1000, mcmc=10000として,グラフがどの様になっていくかを示してみよう(スクリプトは省略,グラフも真ん中の factor(sex)2 のもののみ)。



以下では,burnin=1000として最初の1000個の数字は捨ててmcmc=100000としてそれぞれ100000個の数字からなる異なる系列を3つ生成した上で10個おきの数字だけを採用し(thin=10,3系列を1つに纏めた上で図示し,且つ summary( )で計算結果の数字を確認しよう。また,収束しているか否か(きちんとした信頼できる結果が得られているか否か)を診断する関数も付記だけしておく(収束診断の結果は省略)。
b1 <- MCMCregress(q1700b ~ factor(sex), data=data01,
burnin=1000, mcmc=100000, thin=10, seed=1234)
b2 <- MCMCregress(q1700b ~ factor(sex), data=data01,
burnin=1000, mcmc=100000, thin=10, seed=2345)
b3 <- MCMCregress(q1700b ~ factor(sex), data=data01,
burnin=1000, mcmc=100000, thin=10, seed=3456)
chains <- mcmc.list(b1, b2, b3) # 複数の系列を一つに纏める
plot(chains, smooth=F)
summary(chains)
# 3種の収束診断
raftery.diag(chains)
gelman.diag(chains)
geweke.diag(chains)
burnin=1000, mcmc=100000, thin=10, seed=1234)
b2 <- MCMCregress(q1700b ~ factor(sex), data=data01,
burnin=1000, mcmc=100000, thin=10, seed=2345)
b3 <- MCMCregress(q1700b ~ factor(sex), data=data01,
burnin=1000, mcmc=100000, thin=10, seed=3456)
chains <- mcmc.list(b1, b2, b3) # 複数の系列を一つに纏める
plot(chains, smooth=F)
summary(chains)
# 3種の収束診断
raftery.diag(chains)
gelman.diag(chains)
geweke.diag(chains)


切片(Intercept),男性に対する女性の平均差(factor(sex)2),誤差分散(sigma2)のそれぞれについて,10000個の推定値が3系列あるので全部で30000個の推定値が得られ,その事後分布の平均(Mean)や標準偏差(SD),2.5%点や97.5%点が表示されている。
2.5%点から97.5%点の範囲は,頻度主義ではconfidence interval(信頼区間)と呼ぶが,ベイズ統計学においては,credible interval(信用区間或は確信区間)と呼ばれている。ベイズのcredible intervalの解釈は非常に素朴で分かり易く,「母数がその区間に存在する確率が95%である。」と云ったものになる。
この結果を,上のステューデントのt検定または単回帰分析の結果と比較してみると,新しい統計学を導入した割には,結果は殆ど一致しているので拍子抜けするかも知れない。実は,初歩的な重回帰分析くらいでは頻度主義の95%信頼区間とベイズの95%確信区間はほぼ変わらない事が多い。ベイズ統計学を本当に活用する為には,もっと複雑なモデル,前提を置かないモデルなどで柔軟な分析をするのが良いかも知れない。
2-2 重回帰分析
基本的に目新しい内容は出て来ないが,第9章1-1の重回帰分析をベイズで分析してみよう。
まずは,第9章の通常の(OLS)重回帰分析を確認しておく。
この結果には後程戻って来て貰う事として,これと同じモデルを MCMCregress( )で計算しよう。
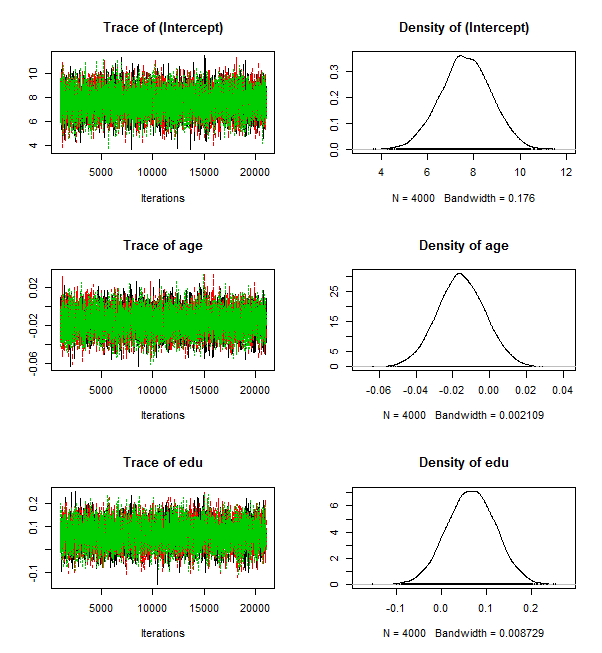
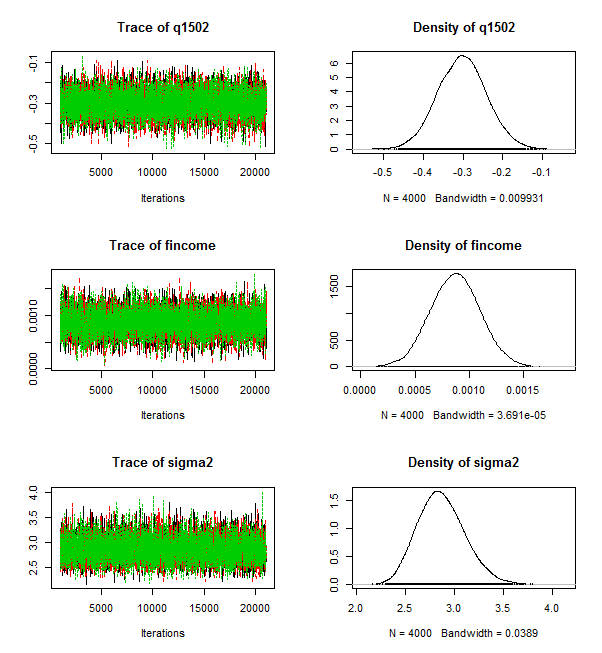
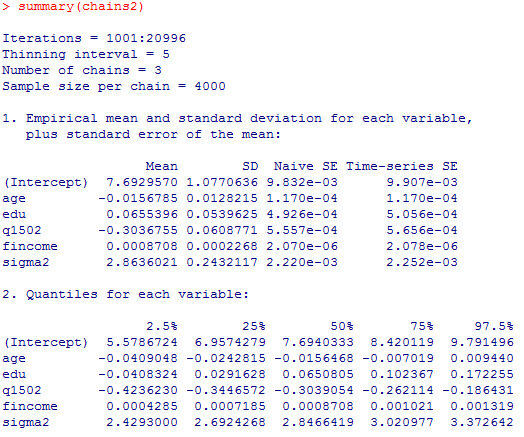
分析結果は,OLS重回帰分析とほぼ一致する。頻度論的推定は,事前分布に前提を置かないベイズ推定とほぼ一致する。
なお,収束診断の結果は省略したが,この場合は必ずしも良好とは言えない様である。モデルを改善する必要がありそうだ。
まずは,第9章の通常の(OLS)重回帰分析を確認しておく。
# 重回帰分析(第9章)
reg0901 <- lm(q1700b ~ age + edu + q1502 + fincome, data=data01)
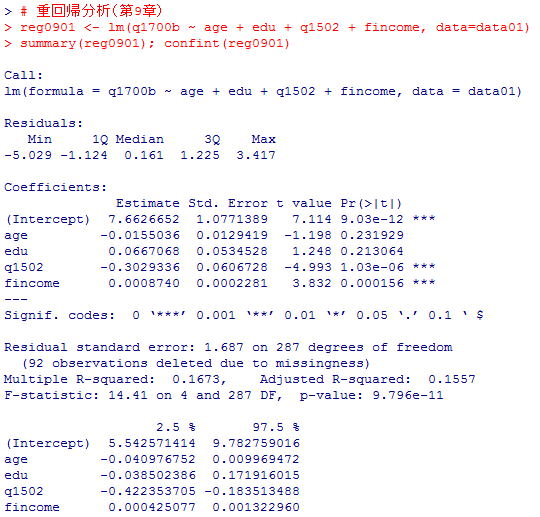
summary(reg0901); confint(reg0901)
reg0901 <- lm(q1700b ~ age + edu + q1502 + fincome, data=data01)
summary(reg0901); confint(reg0901)

この結果には後程戻って来て貰う事として,これと同じモデルを MCMCregress( )で計算しよう。
b21 <- MCMCregress(q1700b ~ age + edu + q1502 + fincome, data=data01,
burnin=1000, mcmc=20000, thin=5, seed=4567)
b22 <- MCMCregress(q1700b ~ age + edu + q1502 + fincome, data=data01,
burnin=1000, mcmc=20000, thin=5, seed=5678)
b23 <- MCMCregress(q1700b ~ age + edu + q1502 + fincome, data=data01,
burnin=1000, mcmc=20000, thin=5, seed=6789)
chains2 <- mcmc.list(b21, b22, b23) # 複数の系列を一つに纏める
plot(chains2, smooth=F)
summary(chains2)
# 収束診断
raftery.diag(chains2)
gelman.diag(chains2)
geweke.diag(chains2)
burnin=1000, mcmc=20000, thin=5, seed=4567)
b22 <- MCMCregress(q1700b ~ age + edu + q1502 + fincome, data=data01,
burnin=1000, mcmc=20000, thin=5, seed=5678)
b23 <- MCMCregress(q1700b ~ age + edu + q1502 + fincome, data=data01,
burnin=1000, mcmc=20000, thin=5, seed=6789)
chains2 <- mcmc.list(b21, b22, b23) # 複数の系列を一つに纏める
plot(chains2, smooth=F)
summary(chains2)
# 収束診断
raftery.diag(chains2)
gelman.diag(chains2)
geweke.diag(chains2)



分析結果は,OLS重回帰分析とほぼ一致する。頻度論的推定は,事前分布に前提を置かないベイズ推定とほぼ一致する。
なお,収束診断の結果は省略したが,この場合は必ずしも良好とは言えない様である。モデルを改善する必要がありそうだ。
2-3 2項ロジスティック回帰
第12章1-3の2項ロジスティック回帰(2項ロジット)も,MCMClogit( )でほぼ同様に分析する事が出来,事前確率分布に特に条件を設定しない限り,頻度論的なロジスティック回帰分析の結果とほぼ同様となる。
データの読み込みや変数作成の部分は省略する。#の後のコメント分は邪魔ならなくて良い。
次は,或時点の値とそれとlagだけ離れた時点の値の相関係数(自己相関)を,1番目のチェイン(BL1)についてだけ,切片を除いて描画したものである。0に近づいていれば問題無い。
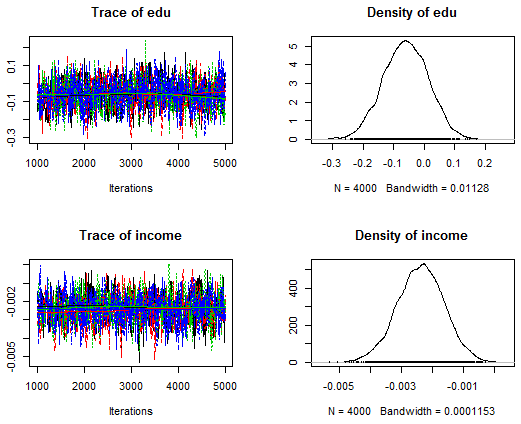
次のグラフは,トレースプロットと密度プロットと呼ばれるもので,前者が一つの帯の様になっていれば問題無く,密度グラフがベイズ信用区間(確信区間)を視覚化している。スペース節約の為切片は省略した。
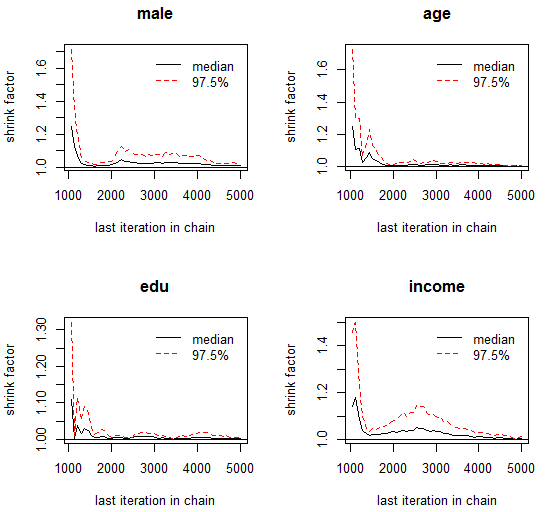
最後は,Gelman法の収束診断についての図示である。これも切片は省略した。1.1以下で許容可能と言われている様だ。
データの読み込みや変数作成の部分は省略する。#の後のコメント分は邪魔ならなくて良い。
library(MCMCpack) # Rを起動後1回だけ読み込めば良い
bu0 <- 1000; mc0 <- 4000; th0 <- 1 # 初期値依存の為に捨てる長さ(burnin),繰り返しの長さ(mcmc),推定値を拾う間隔(thin)の設定
sds <- c(123, 234, 345, 456) # 乱数のシードをチェイン毎に指定。数字は何でも良い
BL1 <- MCMClogit(single ~ male + age + edu + income,
burnin=bu0, mcmc=mc0, thin=th0, seed=sds[1])
BL2 <- MCMClogit(single ~ male + age + edu + income,
burnin=bu0, mcmc=mc0, thin=th0, seed=sds[2])
BL3 <- MCMClogit(single ~ male + age + edu + income,
burnin=bu0, mcmc=mc0, thin=th0, seed=sds[3])
BL4 <- MCMClogit(single ~ male + age + edu + income,
burnin=bu0, mcmc=mc0, thin=th0, seed=sds[4])
BL <- mcmc.list(BL1, BL2, BL3, BL4) # 4つのチェインを一つに纏める
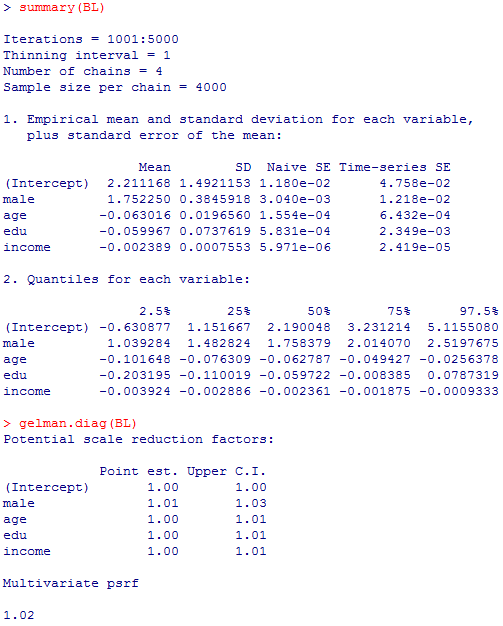
summary(BL)
gelman.diag(BL)
autocorr.plot(BL1[, 2:5]) # 一つ目のチェインの切片以外について,自己相関の変化を描画
plot(BL, ask=dev.interactive()) # 画面が何枚にも分かれる場合に,1枚ずつ確認
gelman.plot(BL[, 2:5])
まずはコンソール画面の計算結果。第12章1-3の glm( , family = binomial(link = "logit")) の結果とほぼ一致する(よっていまいち有難みは感じられないが…)。ついでに何種類かある収束判定方法の一つGelman法の計算結果も。bu0 <- 1000; mc0 <- 4000; th0 <- 1 # 初期値依存の為に捨てる長さ(burnin),繰り返しの長さ(mcmc),推定値を拾う間隔(thin)の設定
sds <- c(123, 234, 345, 456) # 乱数のシードをチェイン毎に指定。数字は何でも良い
BL1 <- MCMClogit(single ~ male + age + edu + income,
burnin=bu0, mcmc=mc0, thin=th0, seed=sds[1])
BL2 <- MCMClogit(single ~ male + age + edu + income,
burnin=bu0, mcmc=mc0, thin=th0, seed=sds[2])
BL3 <- MCMClogit(single ~ male + age + edu + income,
burnin=bu0, mcmc=mc0, thin=th0, seed=sds[3])
BL4 <- MCMClogit(single ~ male + age + edu + income,
burnin=bu0, mcmc=mc0, thin=th0, seed=sds[4])
BL <- mcmc.list(BL1, BL2, BL3, BL4) # 4つのチェインを一つに纏める
summary(BL)
gelman.diag(BL)
autocorr.plot(BL1[, 2:5]) # 一つ目のチェインの切片以外について,自己相関の変化を描画
plot(BL, ask=dev.interactive()) # 画面が何枚にも分かれる場合に,1枚ずつ確認
gelman.plot(BL[, 2:5])

次は,或時点の値とそれとlagだけ離れた時点の値の相関係数(自己相関)を,1番目のチェイン(BL1)についてだけ,切片を除いて描画したものである。0に近づいていれば問題無い。

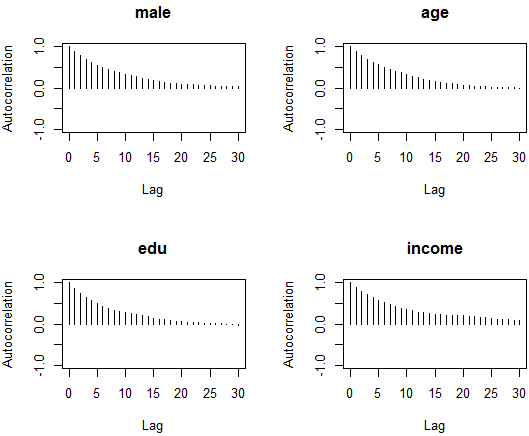
次のグラフは,トレースプロットと密度プロットと呼ばれるもので,前者が一つの帯の様になっていれば問題無く,密度グラフがベイズ信用区間(確信区間)を視覚化している。スペース節約の為切片は省略した。


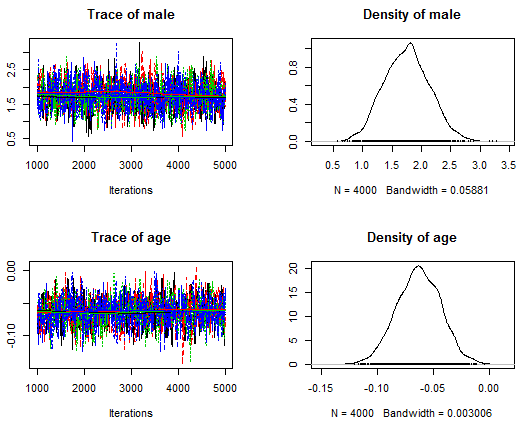
最後は,Gelman法の収束診断についての図示である。これも切片は省略した。1.1以下で許容可能と言われている様だ。

3 RStanによるベイズ統計学的分析
3-1 RとStanによる重回帰分析
上にも述べた様に,rstanのインストールや活用は初級者にはややハードルが高い。下記のサイトや書籍を参照して欲しい(いずれも2017年5月7日閲覧)。
Kentaro Matsuura, 'RStan Getting Started (Japanese): RStanをはじめよう',
松浦健太郎, 2016, 『StanとRでベイズ統計モデリング』, 東京: 共立出版.
ここでは,RStudioは使用せずにプレーンなRで演習する。rstanのinstallまでは出来ているものとして,ごく単純な重回帰分析を行った例を示す。演習用データで,男性ダミーmaleと年齢ageと教育年数eduから個人年収incomeを説明(推定)するモデルを作成する。
RとStanは本来は別々のアプリケイションであり,RのパッケイジrstanはRとStanを繋ぐものであると考えると良い。従って,やや面倒であるが,Stanのコードファイルと,それを呼び出すRのスクリプトファイルの2つを作成する必要がある。
まずはStanのコードファイル(ファイル名を MRA-3IV.stan として保存しておく)。
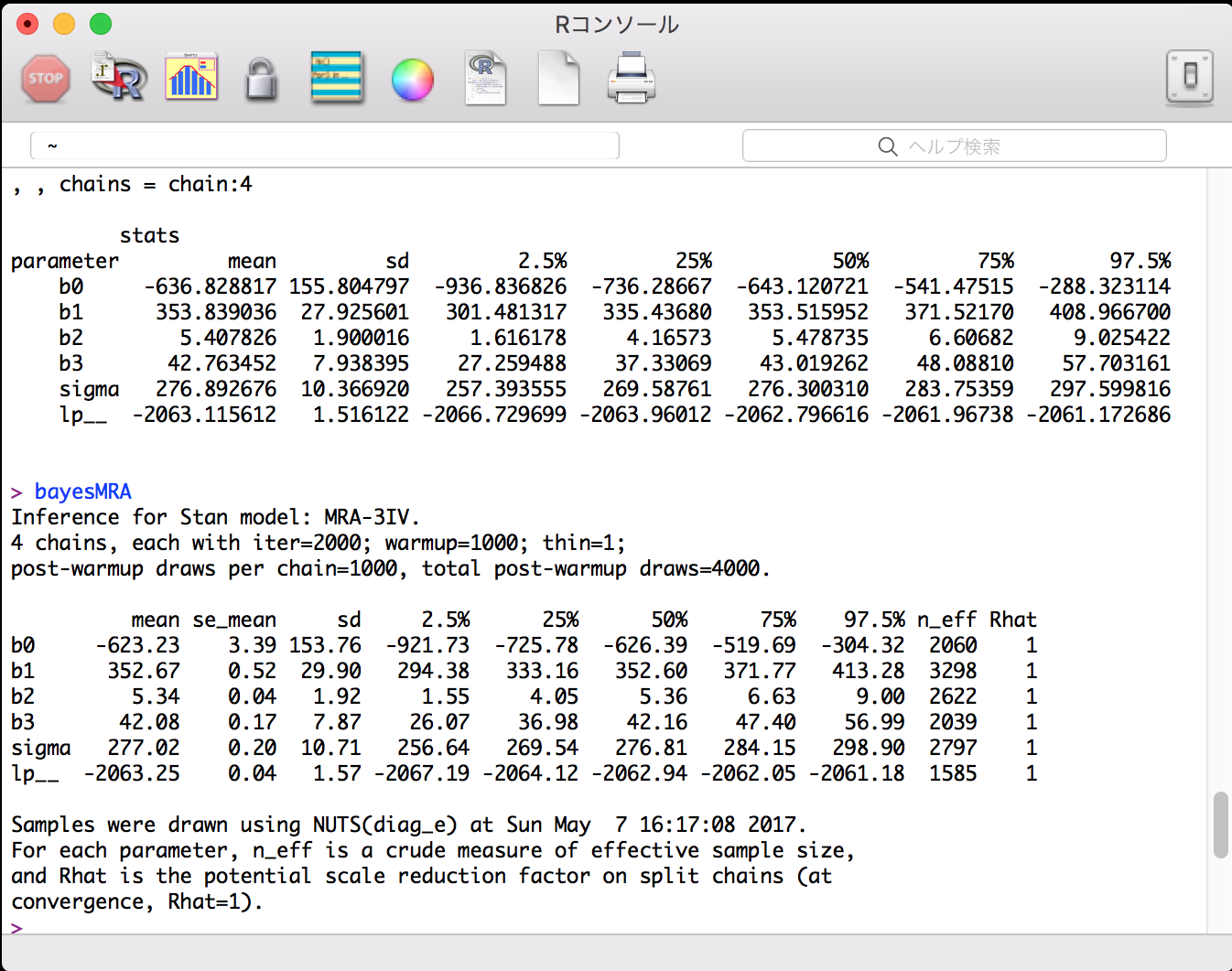
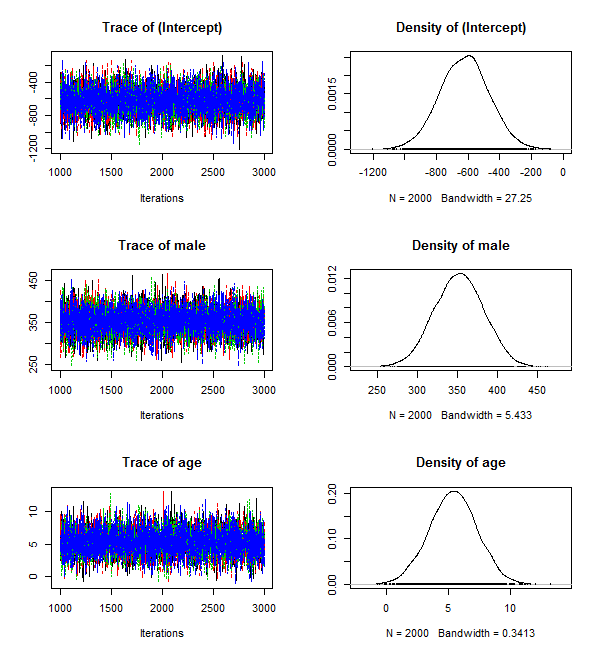
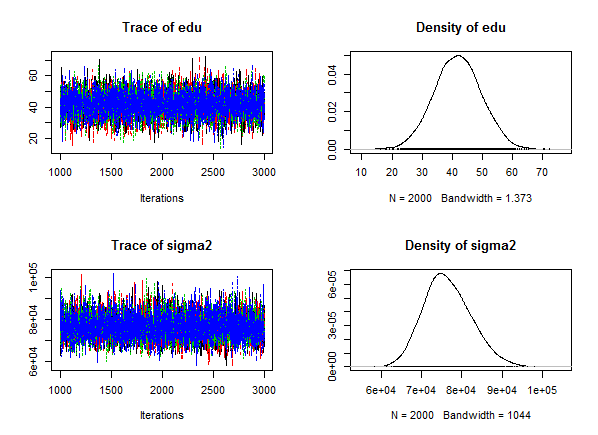
上のRスクリプトのコンソール出力結果。
重要な部分( bayesMRA の行)を中心に,以下に掲示する(Mac版Rのコンソール)。
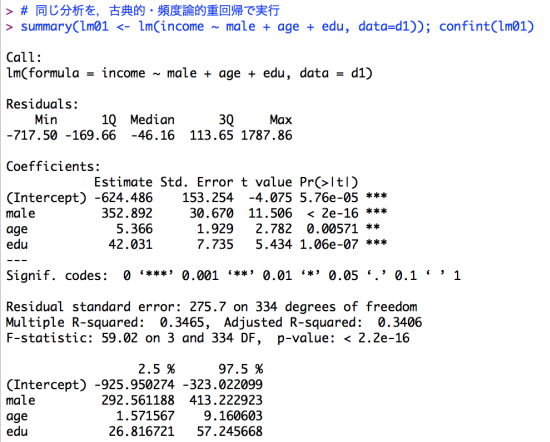
古典的/頻度論的重回帰分析での分析結果は以下である(Mac版Rのコンソール)。
更に,ほぼ条件を揃えた MCMCregress( )での分析結果も示しておく。


いずれの方法でも結果はほぼ同一と言って良い程度であり,この程度の単純な分析ではベイズ統計学(MCMC法による計算)やStanの有用性は余り分からないが,Stanのコードファイルを見ると何となく分かる様に,複雑なモデルを自由に組む程,Stanの有効性が高まると考えられる。
Kentaro Matsuura, 'RStan Getting Started (Japanese): RStanをはじめよう',
松浦健太郎, 2016, 『StanとRでベイズ統計モデリング』, 東京: 共立出版.
ここでは,RStudioは使用せずにプレーンなRで演習する。rstanのinstallまでは出来ているものとして,ごく単純な重回帰分析を行った例を示す。演習用データで,男性ダミーmaleと年齢ageと教育年数eduから個人年収incomeを説明(推定)するモデルを作成する。
RとStanは本来は別々のアプリケイションであり,RのパッケイジrstanはRとStanを繋ぐものであると考えると良い。従って,やや面倒であるが,Stanのコードファイルと,それを呼び出すRのスクリプトファイルの2つを作成する必要がある。
まずはStanのコードファイル(ファイル名を MRA-3IV.stan として保存しておく)。
data {
int N;
vector[N] X1;
vector[N] X2;
vector[N] X3;
vector[N] Y;
}
parameters {
real b0;
real b1;
real b2;
real b3;
real<lower=0> sigma;
}
model {
Y ~ normal(b0 + b1*X1 + b2*X2 + b3*X3, sigma);
}
次に,これを呼び出すRのスクリプトである(→Mac用Rのエディタでの表示画面)。int N;
vector[N] X1;
vector[N] X2;
vector[N] X3;
vector[N] Y;
}
parameters {
real b0;
real b1;
real b2;
real b3;
real<lower=0> sigma;
}
model {
Y ~ normal(b0 + b1*X1 + b2*X2 + b3*X3, sigma);
}
library(rstan) # Rでベイズ推計を行うパッケイジrstanを読み込む
# 演習用データフレイムの読み込み
d0 <- read.csv("documents/practice.csv")
names(d0)
# 以下で使用する4つの変数がmissingでないケースだけを残す
d1 <- d0[complete.cases(d0$income, d0$sex, d0$age, d0$edu),]
d1$male <- c(1, 0)[d1$sex] # 男性ダミー変数の作成
# rstan( )関数に渡すデータをリスト形式で準備
data02 <- list(N=nrow(d1), X1=d1$male, X2=d1$age, X3=d1$edu, Y=d1$income)
data02 # 一応,中身を確認
# rstanの結果をオブジェクト保存。seed=は乱数の種の番号で特に意味は無い
bayesMRA <- stan(file='MRA-3IV.stan', data=data02, seed=5978)
# 結果は,summary( )の方が詳しく表示され,オブジェクト名だけを指示すると最終結果のみ
summary(bayesMRA)
bayesMRA
# 同じ分析を,古典的・頻度論的重回帰で実行
summary(lm01 <- lm(income ~ male + age + edu, data=d1)); confint(lm01)
この出力結果は長大になるので,テキストファイルで別ウィンドウで見て欲しい。# 演習用データフレイムの読み込み
d0 <- read.csv("documents/practice.csv")
names(d0)
# 以下で使用する4つの変数がmissingでないケースだけを残す
d1 <- d0[complete.cases(d0$income, d0$sex, d0$age, d0$edu),]
d1$male <- c(1, 0)[d1$sex] # 男性ダミー変数の作成
# rstan( )関数に渡すデータをリスト形式で準備
data02 <- list(N=nrow(d1), X1=d1$male, X2=d1$age, X3=d1$edu, Y=d1$income)
data02 # 一応,中身を確認
# rstanの結果をオブジェクト保存。seed=は乱数の種の番号で特に意味は無い
bayesMRA <- stan(file='MRA-3IV.stan', data=data02, seed=5978)
# 結果は,summary( )の方が詳しく表示され,オブジェクト名だけを指示すると最終結果のみ
summary(bayesMRA)
bayesMRA
# 同じ分析を,古典的・頻度論的重回帰で実行
summary(lm01 <- lm(income ~ male + age + edu, data=d1)); confint(lm01)
上のRスクリプトのコンソール出力結果。
重要な部分( bayesMRA の行)を中心に,以下に掲示する(Mac版Rのコンソール)。

古典的/頻度論的重回帰分析での分析結果は以下である(Mac版Rのコンソール)。

更に,ほぼ条件を揃えた MCMCregress( )での分析結果も示しておく。
# library(MCMCpack)
b1 <- MCMCregress(income ~ male + age +edu, data=data01,
burnin=1000, mcmc=2000, thin=1, seed=1234)
b2 <- MCMCregress(income ~ male + age +edu, data=data01,
burnin=1000, mcmc=2000, thin=1, seed=1342)
b3 <- MCMCregress(income ~ male + age +edu, data=data01,
burnin=1000, mcmc=2000, thin=1, seed=1423)
b4 <- MCMCregress(income ~ male + age +edu, data=data01,
burnin=1000, mcmc=2000, thin=1, seed=1432)
chains <- mcmc.list(b1, b2, b3, b4) # 複数の系列を一つに纏める
plot(chains, smooth=F)
summary(chains)
# 収束診断
gelman.diag(chains)
b1 <- MCMCregress(income ~ male + age +edu, data=data01,
burnin=1000, mcmc=2000, thin=1, seed=1234)
b2 <- MCMCregress(income ~ male + age +edu, data=data01,
burnin=1000, mcmc=2000, thin=1, seed=1342)
b3 <- MCMCregress(income ~ male + age +edu, data=data01,
burnin=1000, mcmc=2000, thin=1, seed=1423)
b4 <- MCMCregress(income ~ male + age +edu, data=data01,
burnin=1000, mcmc=2000, thin=1, seed=1432)
chains <- mcmc.list(b1, b2, b3, b4) # 複数の系列を一つに纏める
plot(chains, smooth=F)
summary(chains)
# 収束診断
gelman.diag(chains)




いずれの方法でも結果はほぼ同一と言って良い程度であり,この程度の単純な分析ではベイズ統計学(MCMC法による計算)やStanの有用性は余り分からないが,Stanのコードファイルを見ると何となく分かる様に,複雑なモデルを自由に組む程,Stanの有効性が高まると考えられる。
3-2 RとStanでWelch検定と同じ分析をベイズで行う
もう少しrstanの説明を補おう。重回帰分析を例示した後で二群の母平均の差の推測をするのはやや順序が逆にも思えるが,より基本的な分析に立ち戻って初歩から理解しよう。
頻度論の検定では,二群の母分散が等しいと言えるか言えないかで場合分けをする習慣がかつてはあり,母分散が等しければStudentのt検定,母分散が等しいとは言えなければWelchのt検定を行う事が多かった。その後,等分散であるか否かを確認せずに(検定の多重性を回避して)最初からWelch検定を行う事が主流となった。
Stanを用いた分析では,そもそも等分散を仮定する必要が無いので(仮定したければ勿論そう出来る),最初からWelchと同じアプローチを取る事になる。
最初にStanのコードファイル(青の背景),そして次にそれを呼び出すRのスクリプトファイル(黄色の背景)を示す。
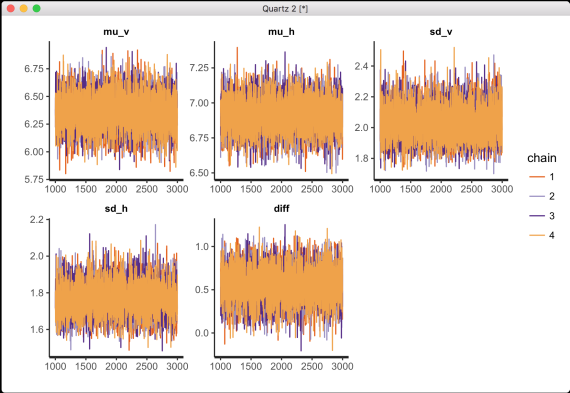
次が stan_trace( ) の出力。問題無く収束しているかどうかを目視する。chain毎に描き分けている。
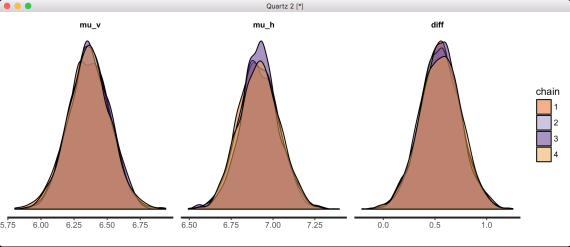
stan_histの出力は省略し,次は stan_dens( ) の出力。
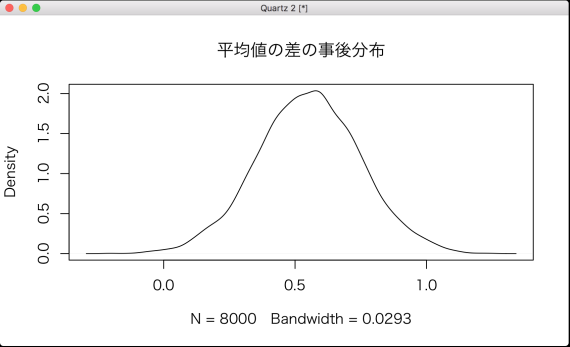
次は plot(density(data04$diff), main="平均値の差の事後分布") の結果。
最後に,「# 二つの平均値の事後分布をヒストグラムで重ね描き」以下の描画結果。
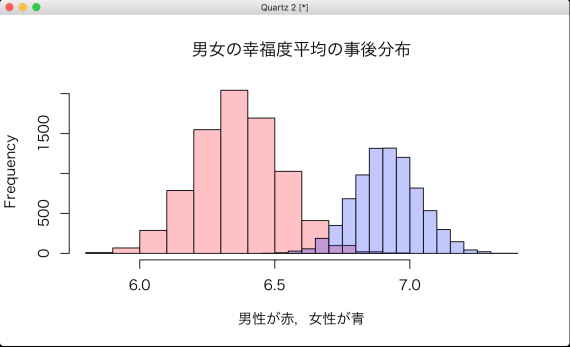
男性の幸福度平均も女性の幸福度平均もそれぞれバラつきはあるが,ほぼ確実に女性の幸福度の方が高い事が読み取れる。Rスクリプトの post_prob の部分で,女性の幸福度平均 マイナス 男性の幸福度平均 の事後分布が0より大きくなる確率を計算している。結果は省略しているが,99%以上となる。
頻度論的なスチューデントのt検定,Welch検定の結果は以下の通りである。Student検定とWelch検定の違いも大きくはないが,上のrstanの結果(オブジェクト"bayes_welch"のコンソール出力)と見比べると,Welch検定の差の95%信頼区間とベイズ分析の95%信用区間の方が僅かに近くなっている。また,ベイズ推計では,二群の母標準偏差もそれぞれ2.03,1.77と具体的に推計されている。分散比にすれば1.3倍余りである。

結果の貼り付けだけになるが,これらを参考にすれば,MCMCpackパッケイジの plot( ) と同じかそれ以上のグラフを rstan で作成出来るだろう。
頻度論の検定では,二群の母分散が等しいと言えるか言えないかで場合分けをする習慣がかつてはあり,母分散が等しければStudentのt検定,母分散が等しいとは言えなければWelchのt検定を行う事が多かった。その後,等分散であるか否かを確認せずに(検定の多重性を回避して)最初からWelch検定を行う事が主流となった。
Stanを用いた分析では,そもそも等分散を仮定する必要が無いので(仮定したければ勿論そう出来る),最初からWelchと同じアプローチを取る事になる。
最初にStanのコードファイル(青の背景),そして次にそれを呼び出すRのスクリプトファイル(黄色の背景)を示す。
// ファイル名は bayes_welch.stan としておく。
data {
int N1;
int N2;
real X1[N1];
real X2[N2];
}
parameters {
real<lower=0, upper=10> mu_v; // mu_vと云う名前に意味はない
real<lower=0, upper=10> mu_h; // mu_hと云う名前に意味はない
real<lower=0> sd_v;
real<lower=0> sd_h;
}
model {
mu_v ~ uniform(0, 10); // 第1群の母平均の事前分布
mu_h ~ uniform(0, 10); // 第2群の母平均の事前分布
sd_v ~ cauchy(0, 5); // 第1群の母標準偏差の事前分布
sd_h ~ cauchy(0, 5); // 第2群の母標準偏差の事前分布
X1 ~ normal(mu_v, sd_v); // 第1群の測定値が正規分布から発生
X2 ~ normal(mu_h, sd_h); // 第2群の測定値が正規分布から発生
}
generated quantities {
real diff;
diff = mu_h - mu_v; // 母平均の差を生成量として保存しておく
}
次は,このStanコード(bayes_welch.stan)を呼び出すRのスクリプトファイルである。data {
int N1;
int N2;
real X1[N1];
real X2[N2];
}
parameters {
real<lower=0, upper=10> mu_v; // mu_vと云う名前に意味はない
real<lower=0, upper=10> mu_h; // mu_hと云う名前に意味はない
real<lower=0> sd_v;
real<lower=0> sd_h;
}
model {
mu_v ~ uniform(0, 10); // 第1群の母平均の事前分布
mu_h ~ uniform(0, 10); // 第2群の母平均の事前分布
sd_v ~ cauchy(0, 5); // 第1群の母標準偏差の事前分布
sd_h ~ cauchy(0, 5); // 第2群の母標準偏差の事前分布
X1 ~ normal(mu_v, sd_v); // 第1群の測定値が正規分布から発生
X2 ~ normal(mu_h, sd_h); // 第2群の測定値が正規分布から発生
}
generated quantities {
real diff;
diff = mu_h - mu_v; // 母平均の差を生成量として保存しておく
}
data01 <- read.csv("practice.csv")
names(data01)
# 幸福度q1700の処理
data01$q1700b <- c(0:10)[data01$q1700+1] # recode方法に若干の工夫
t01 <- t.test(data01$q1700b ~ data01$sex, var.equal=T) # Studentのt検定
w01 <- t.test(data01$q1700b ~ data01$sex, var.equal=F) # Welchのt検定
t01; w01
happy_m <- data01$q1700b[data01$sex == 1 & !is.na(data01$q1700b)]
happy_f <- data01$q1700b[data01$sex == 2 & !is.na(data01$q1700b)]
# library(rstan)
# rstan( )関数に渡すデータをリスト形式で準備
n1 <- length(happy_m)
n2 <- length(happy_f)
data_r <- list(N1=n1, N2=n2, X1=happy_m, X2=happy_f)
# rstanの結果をオブジェクト保存。seed=は乱数の種の番号で特に意味は無い
bayes_welch <- stan(file='bayes_welch.stan', data=data_r, seed=5171,
chains=4, iter=3000, warmup=1000)
bayes_welch
stan_trace(bayes_welch)
stan_hist(bayes_welch, par=c("mu_v", "mu_h"))
stan_dens(bayes_welch, par=c("mu_v", "mu_h", "diff"), separate_chains=T)
stan_ac(bayes_welch)
result <- rstan::extract(bayes_welch)
data04 <- data.frame(mu_v=result$mu_v, mu_h=result$mu_h, diff=result$diff)
post_prob <- sum(data04$diff > 0)/nrow(data04)
post_prob
par(family="HiraKakuPro-W3") # Macにおけるグラフの文字化け対策
plot(density(data04$diff), main="平均値の差の事後分布")
# 二つの平均値の事後分布をヒストグラムで重ね描き
x_min <- min(data04$mu_v, data04$mu_h)
x_max <- max(data04$mu_v, data04$mu_h)
hist(data04$mu_v, xlim=c(x_min, x_max), col="#ff000040", main="男女の幸福度平均の事後分布", xlab="男性が赤,女性が青")
hist(data04$mu_h, xlim=c(x_min, x_max), col="#0000ff40", add=T)
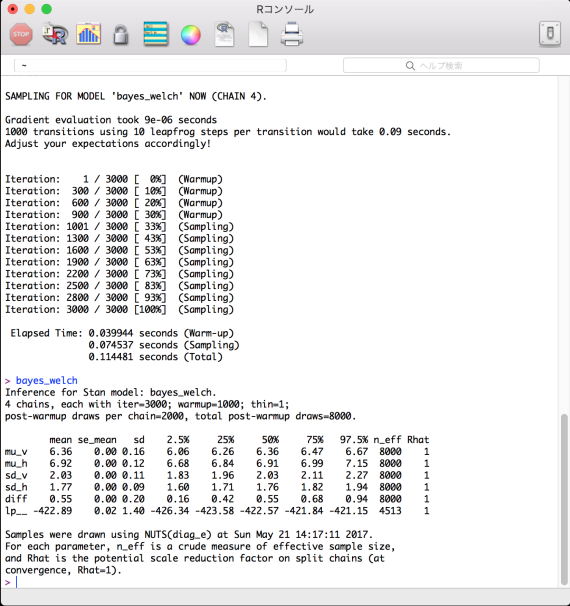
オブジェクト bayes_welch のMac上のRでの表示。その上には計算過程のコンソール出力の最後の辺りが表示されている。names(data01)
# 幸福度q1700の処理
data01$q1700b <- c(0:10)[data01$q1700+1] # recode方法に若干の工夫
t01 <- t.test(data01$q1700b ~ data01$sex, var.equal=T) # Studentのt検定
w01 <- t.test(data01$q1700b ~ data01$sex, var.equal=F) # Welchのt検定
t01; w01
happy_m <- data01$q1700b[data01$sex == 1 & !is.na(data01$q1700b)]
happy_f <- data01$q1700b[data01$sex == 2 & !is.na(data01$q1700b)]
# library(rstan)
# rstan( )関数に渡すデータをリスト形式で準備
n1 <- length(happy_m)
n2 <- length(happy_f)
data_r <- list(N1=n1, N2=n2, X1=happy_m, X2=happy_f)
# rstanの結果をオブジェクト保存。seed=は乱数の種の番号で特に意味は無い
bayes_welch <- stan(file='bayes_welch.stan', data=data_r, seed=5171,
chains=4, iter=3000, warmup=1000)
bayes_welch
stan_trace(bayes_welch)
stan_hist(bayes_welch, par=c("mu_v", "mu_h"))
stan_dens(bayes_welch, par=c("mu_v", "mu_h", "diff"), separate_chains=T)
stan_ac(bayes_welch)
result <- rstan::extract(bayes_welch)
data04 <- data.frame(mu_v=result$mu_v, mu_h=result$mu_h, diff=result$diff)
post_prob <- sum(data04$diff > 0)/nrow(data04)
post_prob
par(family="HiraKakuPro-W3") # Macにおけるグラフの文字化け対策
plot(density(data04$diff), main="平均値の差の事後分布")
# 二つの平均値の事後分布をヒストグラムで重ね描き
x_min <- min(data04$mu_v, data04$mu_h)
x_max <- max(data04$mu_v, data04$mu_h)
hist(data04$mu_v, xlim=c(x_min, x_max), col="#ff000040", main="男女の幸福度平均の事後分布", xlab="男性が赤,女性が青")
hist(data04$mu_h, xlim=c(x_min, x_max), col="#0000ff40", add=T)

次が stan_trace( ) の出力。問題無く収束しているかどうかを目視する。chain毎に描き分けている。

stan_histの出力は省略し,次は stan_dens( ) の出力。

次は plot(density(data04$diff), main="平均値の差の事後分布") の結果。

最後に,「# 二つの平均値の事後分布をヒストグラムで重ね描き」以下の描画結果。

男性の幸福度平均も女性の幸福度平均もそれぞれバラつきはあるが,ほぼ確実に女性の幸福度の方が高い事が読み取れる。Rスクリプトの post_prob の部分で,女性の幸福度平均 マイナス 男性の幸福度平均 の事後分布が0より大きくなる確率を計算している。結果は省略しているが,99%以上となる。
頻度論的なスチューデントのt検定,Welch検定の結果は以下の通りである。Student検定とWelch検定の違いも大きくはないが,上のrstanの結果(オブジェクト"bayes_welch"のコンソール出力)と見比べると,Welch検定の差の95%信頼区間とベイズ分析の95%信用区間の方が僅かに近くなっている。また,ベイズ推計では,二群の母標準偏差もそれぞれ2.03,1.77と具体的に推計されている。分散比にすれば1.3倍余りである。

結果の貼り付けだけになるが,これらを参考にすれば,MCMCpackパッケイジの plot( ) と同じかそれ以上のグラフを rstan で作成出来るだろう。
3-3 RとStanでマルチレヴェル
第13章1-2 マルチレヴェルモデルで例示したモデルを,rstanでも再現してみる。
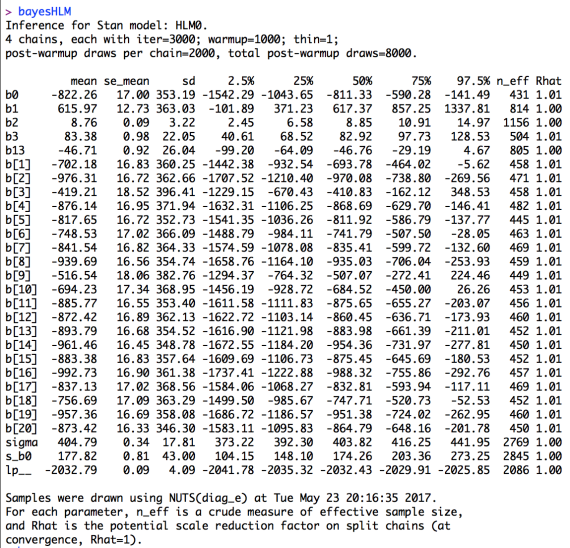
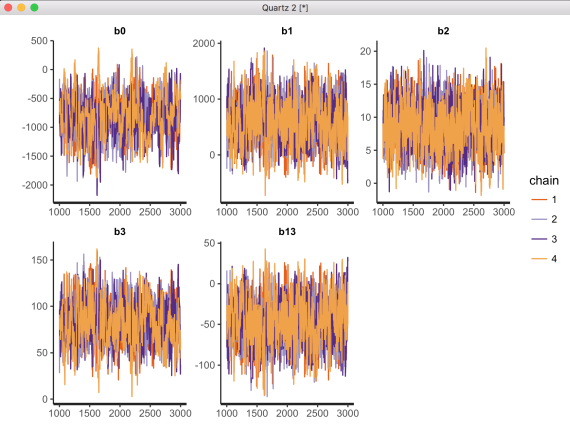
stan_trace(bayesHLM, pars=c("b0", "b1", "b2", "b3", "b13")) の描画結果。これまでの例と比べると,やや収束が悪い(どのchainも同じ様な帯になってはいない)様に見える。
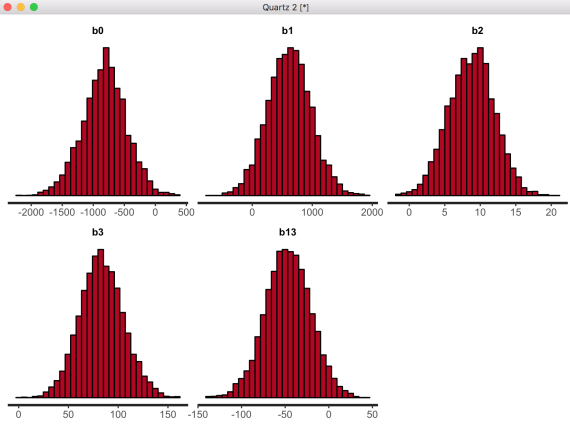
stan_hist(bayesHLM, pars=c("b0", "b1", "b2", "b3", "b13")) の描画結果。
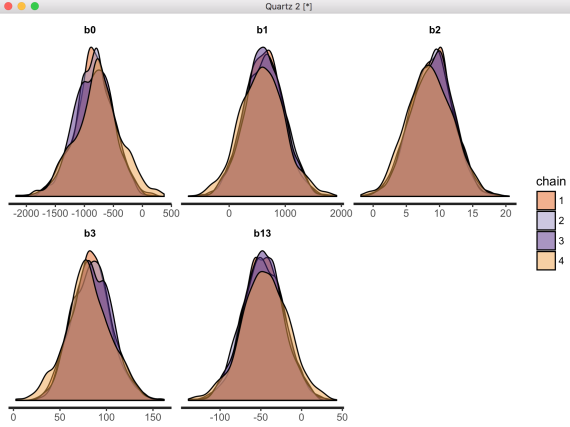
stan_dens(bayesHLM, pars=c("b0", "b1", "b2", "b3", "b13"), separate_chains=T) の描画結果。chainごとの違いがやや目につく。
stan_ac( ) の描画結果は省略するが,自己相関の低下も遅い/十分でない可能性が伺われる。
// ファイル名は HLM0.stan とする。
data {
int N;
int K;
int<lower=0, upper=1> X1[N];
real X2[N];
real X3[N];
int<lower=1, upper=20> Z1[N];
real<lower=0> Y[N];
}
parameters {
real b0;
real b1;
real b2;
real b3;
real b13;
real b[K];
real<lower=0> sigma;
real<lower=0> s_b0;
}
model {
for (k in 1:K) {
b[k] ~ normal(b0, s_b0);
}
for (i in 1:N) {
Y[i] ~ normal(b[Z1[i]] + b1*X1[i] + b2*X2[i] + b3*X3[i] + b13*X1[i]*X3[i], sigma);
}
sigma ~ cauchy(0, 2.5);
s_b0 ~ cauchy(0, 2.5);
}
以下が,このStanコードファイルを呼び出すRスクリプトである。データの読み込みやmaleダミー変数,地点変数の作成の部分は第13章1-1と同じなので省略する。data {
int N;
int K;
int<lower=0, upper=1> X1[N];
real X2[N];
real X3[N];
int<lower=1, upper=20> Z1[N];
real<lower=0> Y[N];
}
parameters {
real b0;
real b1;
real b2;
real b3;
real b13;
real b[K];
real<lower=0> sigma;
real<lower=0> s_b0;
}
model {
for (k in 1:K) {
b[k] ~ normal(b0, s_b0);
}
for (i in 1:N) {
Y[i] ~ normal(b[Z1[i]] + b1*X1[i] + b2*X2[i] + b3*X3[i] + b13*X1[i]*X3[i], sigma);
}
sigma ~ cauchy(0, 2.5);
s_b0 ~ cauchy(0, 2.5);
}
data02 <- data01[complete.cases(data01$fincome, data01$male, data01$age, data01$edu, data01$site),]
data03 <- list(N=nrow(data02), K=length(table(data02$site)),
X1=data02$male, X2=data02$age, X3=data02$edu, Y=data02$fincome, Z1=data02$site)
data03
bayesHLM <- stan(file='HLM0.stan', data=data03, seed=5171,
chains=4, iter=3000, warmup=1000)
summary(bayesHLM)
bayesHLM
stan_trace(bayesHLM, pars=c("b0", "b1", "b2", "b3", "b13"))
stan_hist(bayesHLM, pars=c("b0", "b1", "b2", "b3", "b13"))
stan_dens(bayesHLM, pars=c("b0", "b1", "b2", "b3", "b13"), separate_chains=T)
stan_ac(bayesHLM, pars=c("b0", "b1", "b2", "b3", "b13"))
まずは基本となる出力結果である。第13章1-2の結果と見比べて多少係数値は相違するが,95%信用区間の広さに比べれば大した違いではないと言えるだろう。data03 <- list(N=nrow(data02), K=length(table(data02$site)),
X1=data02$male, X2=data02$age, X3=data02$edu, Y=data02$fincome, Z1=data02$site)
data03
bayesHLM <- stan(file='HLM0.stan', data=data03, seed=5171,
chains=4, iter=3000, warmup=1000)
summary(bayesHLM)
bayesHLM
stan_trace(bayesHLM, pars=c("b0", "b1", "b2", "b3", "b13"))
stan_hist(bayesHLM, pars=c("b0", "b1", "b2", "b3", "b13"))
stan_dens(bayesHLM, pars=c("b0", "b1", "b2", "b3", "b13"), separate_chains=T)
stan_ac(bayesHLM, pars=c("b0", "b1", "b2", "b3", "b13"))

stan_trace(bayesHLM, pars=c("b0", "b1", "b2", "b3", "b13")) の描画結果。これまでの例と比べると,やや収束が悪い(どのchainも同じ様な帯になってはいない)様に見える。

stan_hist(bayesHLM, pars=c("b0", "b1", "b2", "b3", "b13")) の描画結果。

stan_dens(bayesHLM, pars=c("b0", "b1", "b2", "b3", "b13"), separate_chains=T) の描画結果。chainごとの違いがやや目につく。

stan_ac( ) の描画結果は省略するが,自己相関の低下も遅い/十分でない可能性が伺われる。
Copyright (C) 2016-2017 SUGINO Isamu All Rights Reserved. design by tempnate

