杉野 勇 (SUGINO Isamu) お茶の水女子大学・人間発達科学専攻・応用社会学コース担当
『入門・社会統計学』サポートウェブ |
|
 第12章 ロジスティック回帰分析(logistic regression analysis)
第12章 ロジスティック回帰分析(logistic regression analysis)
一般化線型モデル(GLM)の中で社会学では最もポピュラーだと思われるロジスティック回帰分析について説明する。1-1 ロジスティック関数(logistic function)
(未婚である)確率pと(未婚)オッズp/(1-p),そしてその対数オッズlog{p(/1-p)}の関係をグラフで示しておこう。確率は0から1の値しかとりえないのに対して,オッズは論理的には0から+∞,対数オッズは-∞から+∞の値をとり得る。この対数オッズは,重回帰分析の従属変数(被説明変数)とするのに不都合はない。
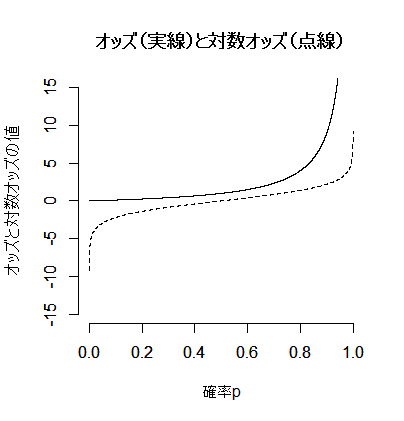
p <- seq(0, 1, by=.0001) # 0から1の確率
odds <- p/(1-p) # オッズ
log_odds <- log(odds) # 対数オッズ
plot(p, odds, ylim=c(-15, 15), xlim=c(0, 1), type="l",
main="オッズ(実線)と対数オッズ(点線)", xlab="確率p",
ylab="オッズと対数オッズの値", bty="n")
par(new=T)
plot(p, log_odds, ylim=c(-15, 15), xlim=c(0, 1), type="l",
lty=2, ylab="", xlab="", bty="n")
odds <- p/(1-p) # オッズ
log_odds <- log(odds) # 対数オッズ
plot(p, odds, ylim=c(-15, 15), xlim=c(0, 1), type="l",
main="オッズ(実線)と対数オッズ(点線)", xlab="確率p",
ylab="オッズと対数オッズの値", bty="n")
par(new=T)
plot(p, log_odds, ylim=c(-15, 15), xlim=c(0, 1), type="l",
lty=2, ylab="", xlab="", bty="n")

1-2 最尤法(Maximum Liklihood Estimation)
男性10人,女性10人の標本で,内閣支持者がそれぞれ5人と4人になった場合の,母集団における支持率を最尤法で推定してみよう。
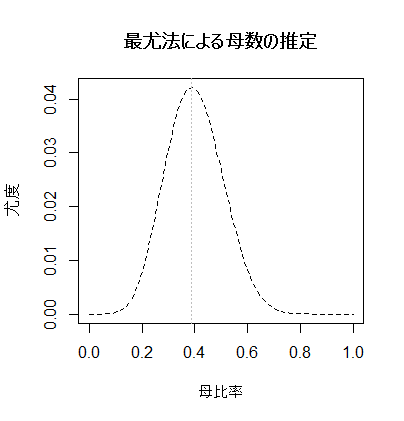
尤度(このような標本が出現する確率)が最大になる母比率は,7/18(男女合わせて18人中7人に相当)である。グラフではグレーの点線で垂直線を書き込んである。
ここで仮に,これまでの調査研究の結果から,母集団における内閣支持率は,女性よりも男性の方が10ポイントだけ高いという事が分かっているとしよう。その場合にこの標本の尤度が最大になる(男性の)母比率は幾つになるだろうか。同様にグラフを描きつつ調べてみよう。
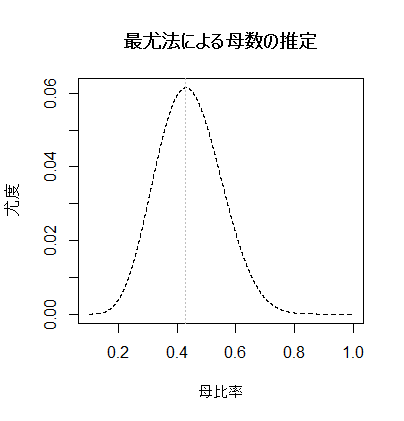
尤度が最大になる母比率の仮説値は次の様に求める事が出来る。上のグラフではこの値で垂直な点線を描いている。

男性の標本支持率は.50,女性の標本支持率は.25であったが,母比率の差が.10であるとの条件の下で最尤法で推定すると,男性の母比率は約.4295,従って女性の母比率は約.3295と推定される事になる。
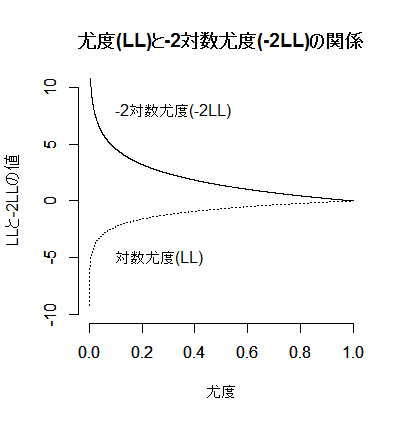
次に,尤度(0〜1)と対数尤度(-∞〜0)の関係をグラフで示す。自然対数は,1に対して0となり,0以上1未満の値に対してはマイナスの値になる。よって対数尤度は基本的にマイナスであり,最大で0になる。但し,尤度が大きければ対数尤度も大きい(マイナスだが絶対値が小さくなる)と云う事は確かである。
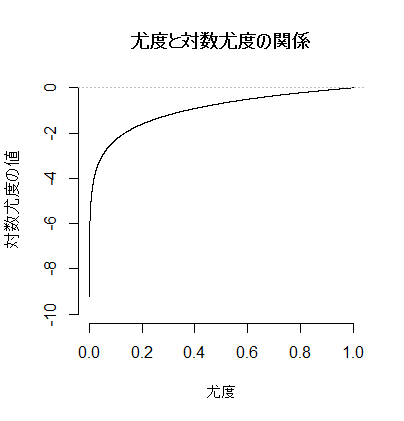
尤度が大きければ対数尤度は大きくなり(マイナスで絶対値が小さくなり)-2対数尤度(逸脱度)はプラスで小さくなる。“より大きな”モデル(独立変数がより多いモデル)と“より小さな”モデルの二つのモデルがあった時,逸脱度は“より大きな”モデルの方が小さい。より小さなモデルの逸脱度とより大きなモデルの逸脱度の差がカイ二乗分布に従う時,その差が有意であれば(偶然とは言えないくらい異なれば),より大きなモデルを採用する。逸脱度の差が有意でなければ(偶然の範囲内である事が否定できなければ),同程度に逸脱しているがより簡潔なモデル,“より小さな”モデルを採用する。
n1 <- 10 # 男性の標本サイズ
n2 <- 8 # 女性の標本サイズ
w1 <- 5 # 男性標本における支持者数
w2 <- 2 # 女性標本における支持者数
pie <- seq(0, 1, by=.01) # 母比率の仮定値
likelihood <- choose(n1, w1)*pie^w1*(1-pie)^(n1-w1)*choose(n2, w2)*pie^w2*(1-pie)^(n2-w2)
plot(pie, likelihood, type="l", lty=2,
xlab="母比率", ylab="尤度", main="最尤法による母数の推定")
n2 <- 8 # 女性の標本サイズ
w1 <- 5 # 男性標本における支持者数
w2 <- 2 # 女性標本における支持者数
pie <- seq(0, 1, by=.01) # 母比率の仮定値
likelihood <- choose(n1, w1)*pie^w1*(1-pie)^(n1-w1)*choose(n2, w2)*pie^w2*(1-pie)^(n2-w2)
plot(pie, likelihood, type="l", lty=2,
xlab="母比率", ylab="尤度", main="最尤法による母数の推定")

尤度(このような標本が出現する確率)が最大になる母比率は,7/18(男女合わせて18人中7人に相当)である。グラフではグレーの点線で垂直線を書き込んである。
ここで仮に,これまでの調査研究の結果から,母集団における内閣支持率は,女性よりも男性の方が10ポイントだけ高いという事が分かっているとしよう。その場合にこの標本の尤度が最大になる(男性の)母比率は幾つになるだろうか。同様にグラフを描きつつ調べてみよう。
pie <- seq(.1, 1, by=.000001) # 母比率の仮定値
likelihood <- choose(n1, w1)*pie^w1*(1-pie)^(n1-w1)*choose(n2, w2)*(pie-.1)^w2*(1-(pie-.1))^(n2-w2)
plot(pie, likelihood, type="l", lty=2,
xlab="母比率", ylab="尤度", main="最尤法による母数の推定")
abline(v=0.4294792, lty=3, col="grey")
likelihood <- choose(n1, w1)*pie^w1*(1-pie)^(n1-w1)*choose(n2, w2)*(pie-.1)^w2*(1-(pie-.1))^(n2-w2)
plot(pie, likelihood, type="l", lty=2,
xlab="母比率", ylab="尤度", main="最尤法による母数の推定")
abline(v=0.4294792, lty=3, col="grey")

尤度が最大になる母比率の仮説値は次の様に求める事が出来る。上のグラフではこの値で垂直な点線を描いている。

男性の標本支持率は.50,女性の標本支持率は.25であったが,母比率の差が.10であるとの条件の下で最尤法で推定すると,男性の母比率は約.4295,従って女性の母比率は約.3295と推定される事になる。
次に,尤度(0〜1)と対数尤度(-∞〜0)の関係をグラフで示す。自然対数は,1に対して0となり,0以上1未満の値に対してはマイナスの値になる。よって対数尤度は基本的にマイナスであり,最大で0になる。但し,尤度が大きければ対数尤度も大きい(マイナスだが絶対値が小さくなる)と云う事は確かである。
l <- seq(0, 1, by=.0001) # 0から1の尤度
log_l <- log(l) # 対数尤度
plot(l, log_l, ylim=c(-10, 0), xlim=c(0, 1), type="l",
main="尤度と対数尤度の関係", xlab="尤度",
ylab="対数尤度の値", bty="n")
abline(h=0, lty=3, col="grey")
log_l <- log(l) # 対数尤度
plot(l, log_l, ylim=c(-10, 0), xlim=c(0, 1), type="l",
main="尤度と対数尤度の関係", xlab="尤度",
ylab="対数尤度の値", bty="n")
abline(h=0, lty=3, col="grey")

plot(l, log_l, ylim=c(-10, 10), xlim=c(0, 1), type="l",
main="尤度(LL)と-2対数尤度(-2LL)の関係", xlab="尤度",
ylab="LLと-2LLの値", bty="n", lty=3)
par(new=T)
plot(l, -2*log_l, ylim=c(-10, 10), xlim=c(0, 1), type="l",
main="", xlab="", ylab="", bty="n")
text(.1, -5, "対数尤度(LL)", adj=0); text(.1, 8, "-2対数尤度(-2LL)", adj=0)
main="尤度(LL)と-2対数尤度(-2LL)の関係", xlab="尤度",
ylab="LLと-2LLの値", bty="n", lty=3)
par(new=T)
plot(l, -2*log_l, ylim=c(-10, 10), xlim=c(0, 1), type="l",
main="", xlab="", ylab="", bty="n")
text(.1, -5, "対数尤度(LL)", adj=0); text(.1, 8, "-2対数尤度(-2LL)", adj=0)

尤度が大きければ対数尤度は大きくなり(マイナスで絶対値が小さくなり)-2対数尤度(逸脱度)はプラスで小さくなる。“より大きな”モデル(独立変数がより多いモデル)と“より小さな”モデルの二つのモデルがあった時,逸脱度は“より大きな”モデルの方が小さい。より小さなモデルの逸脱度とより大きなモデルの逸脱度の差がカイ二乗分布に従う時,その差が有意であれば(偶然とは言えないくらい異なれば),より大きなモデルを採用する。逸脱度の差が有意でなければ(偶然の範囲内である事が否定できなければ),同程度に逸脱しているがより簡潔なモデル,“より小さな”モデルを採用する。
1-3 対数オッズ比(log odds ratio)と2項ロジットモデル(binomial logit model)
男性ダミーと年齢,教育年数,収入によって未婚オッズを推定する2項ロジスティック回帰分析を行ってみよう。
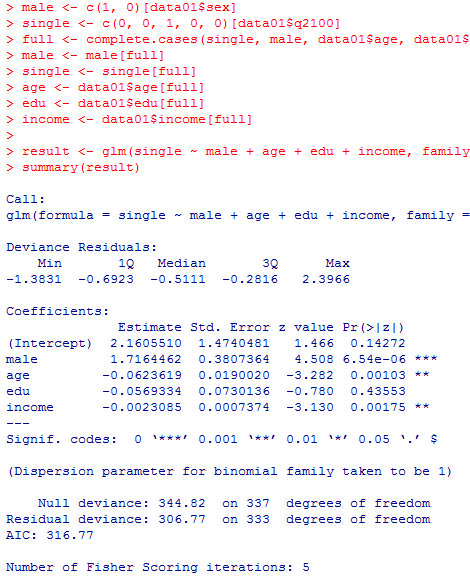
本文の各種オッズ比は次の様に求められる。
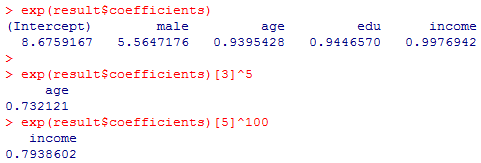
係数の信頼区間,オッズ比の信頼区間は下記。
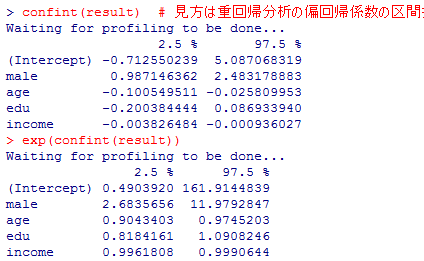
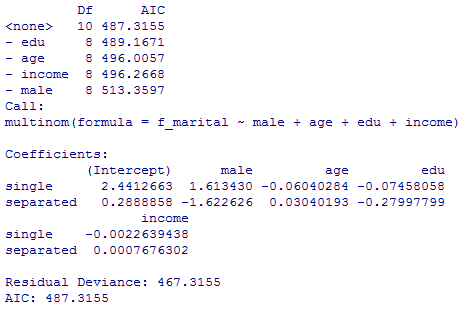
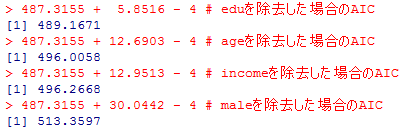
step( )関数による変数選択は下記の様になる。
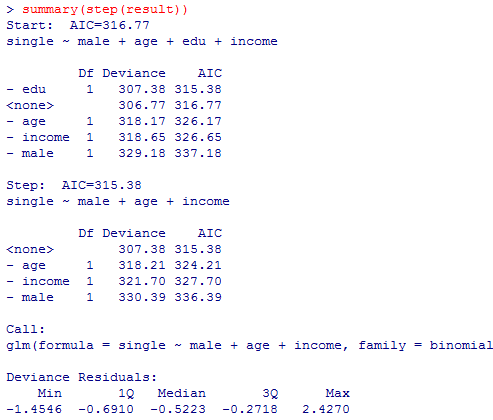
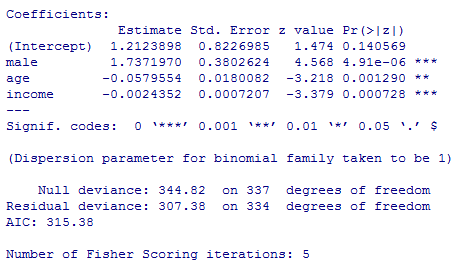
先の初期モデルでは,逸脱度(尤もらしくなさ)が306.77で推定されるパラメタが切片と独立変数の計5つであったので,AIC=-2LL+2p=306.77+2*5=316.77であった(予測の悪さ)。教育年数を除外したモデルでは,AIC=307.38+2*4=315.38で,逸脱度はやや(.61)悪化したが,推定されるパラメタが一つ減った分予測の悪さが2低下し,結果として予測の悪さAICは1.39低下(改善)したのである。逸脱度の悪化分の0.61は自由度1(パラメタ推定値の数の差)のカイ二乗分布に従うが,pchisq(0.61, df=1, lower.tail=F)の結果は 0.4347878で,全く有意ではない。つまり,偶然の範囲内の違いである事が否定できない。
独立変数は全て有意で,係数値は初期モデルと大きな違いは無い。
 Rの"MCMCpack"で二項ロジスティック回帰分析を行った例を,このサポートウェブの〔付録〕2-3で紹介しています。
Rの"MCMCpack"で二項ロジスティック回帰分析を行った例を,このサポートウェブの〔付録〕2-3で紹介しています。
male <- c(1, 0)[data01$sex] # 男性ダミーの作成
single <- c(0, 0, 1, 0, 0)[data01$q2100] # 婚姻上の地位変数から未婚ダミー作成
full <- complete.cases(single, male, data01$age, data01$edu, data01$income) # 欠損値除外
male <- male[full]
single <- single[full]
age <- data01$age[full]
edu <- data01$edu[full]
income <- data01$income[full]
# glm( )関数を用いて二項分布binomial,ロジットリンクlogitを指定
result <- glm(single ~ male + age + edu + income, family = binomial(link = "logit"))
summary(result)
single <- c(0, 0, 1, 0, 0)[data01$q2100] # 婚姻上の地位変数から未婚ダミー作成
full <- complete.cases(single, male, data01$age, data01$edu, data01$income) # 欠損値除外
male <- male[full]
single <- single[full]
age <- data01$age[full]
edu <- data01$edu[full]
income <- data01$income[full]
# glm( )関数を用いて二項分布binomial,ロジットリンクlogitを指定
result <- glm(single ~ male + age + edu + income, family = binomial(link = "logit"))
summary(result)

本文の各種オッズ比は次の様に求められる。

係数の信頼区間,オッズ比の信頼区間は下記。

step( )関数による変数選択は下記の様になる。


先の初期モデルでは,逸脱度(尤もらしくなさ)が306.77で推定されるパラメタが切片と独立変数の計5つであったので,AIC=-2LL+2p=306.77+2*5=316.77であった(予測の悪さ)。教育年数を除外したモデルでは,AIC=307.38+2*4=315.38で,逸脱度はやや(.61)悪化したが,推定されるパラメタが一つ減った分予測の悪さが2低下し,結果として予測の悪さAICは1.39低下(改善)したのである。逸脱度の悪化分の0.61は自由度1(パラメタ推定値の数の差)のカイ二乗分布に従うが,pchisq(0.61, df=1, lower.tail=F)の結果は 0.4347878で,全く有意ではない。つまり,偶然の範囲内の違いである事が否定できない。
独立変数は全て有意で,係数値は初期モデルと大きな違いは無い。
 Rの"MCMCpack"で二項ロジスティック回帰分析を行った例を,このサポートウェブの〔付録〕2-3で紹介しています。
Rの"MCMCpack"で二項ロジスティック回帰分析を行った例を,このサポートウェブの〔付録〕2-3で紹介しています。
1-4 適合度検定(Goodness of Fit Test)と疑似決定係数(Pseudo R-squared)
初期モデルの二項ロジスティック回帰分析の結果(result)について,ホスマー・レムショウの適合度検定を行う為に,ResourceSelectionパッケイジをインストールする。
インストールはinstall.packages("ResourceSelection", repos="https://cran.ism.ac.jp")とする。これはPCにつき1度実行すればよい。パッケイジの読み込みはRの起動のたびにlibrary(ResourceSelection)またはrequire(ResourceSelection)として行う必要がある。BaylorEdPsychパッケイジなど他のパッケイジも同様である。こうした作業に慣れてくれば,Rで出来ることは格段に広がる。

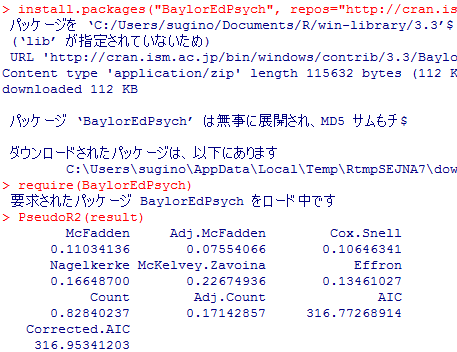
ロジットモデルでよく使われる「疑似決定係数」はBaylorEdPsychパッケイジのPseudoR2( )関数で計算される。
 idre UCLA, 'FAQ: What are pseudo R-squareds?'(2016年11月18日閲覧)
idre UCLA, 'FAQ: What are pseudo R-squareds?'(2016年11月18日閲覧)
この定義式を利用すると,BaylorEdPsychパッケイジをインストールしてPseudoR2( )関数を使用しなくても,以下の様に自分で計算する事が出来る。計算結果を上と比較してみよう。

偏回帰係数の推定の部分やAICは全て一致している。その他,Multiple R-squaredとMcFadden pseudo R2が一致している。
インストールはinstall.packages("ResourceSelection", repos="https://cran.ism.ac.jp")とする。これはPCにつき1度実行すればよい。パッケイジの読み込みはRの起動のたびにlibrary(ResourceSelection)またはrequire(ResourceSelection)として行う必要がある。BaylorEdPsychパッケイジなど他のパッケイジも同様である。こうした作業に慣れてくれば,Rで出来ることは格段に広がる。
install.packages("ResourceSelection", repos="https://cran.ism.ac.jp")
require(ResourceSelection)
names(result)
hoslem.test(result$y, result$fitted.values)
require(ResourceSelection)
names(result)
hoslem.test(result$y, result$fitted.values)

ロジットモデルでよく使われる「疑似決定係数」はBaylorEdPsychパッケイジのPseudoR2( )関数で計算される。
install.packages("BaylorEdPsych", repos="http://cran.ism.ac.jp")
require(BaylorEdPsych)
PseudoR2(result)
require(BaylorEdPsych)
PseudoR2(result)

疑似決定係数の定義と計算
各種の疑似決定係数の定義式は次のサイトを見ると良い。 idre UCLA, 'FAQ: What are pseudo R-squareds?'(2016年11月18日閲覧)
idre UCLA, 'FAQ: What are pseudo R-squareds?'(2016年11月18日閲覧)この定義式を利用すると,BaylorEdPsychパッケイジをインストールしてPseudoR2( )関数を使用しなくても,以下の様に自分で計算する事が出来る。計算結果を上と比較してみよう。
# 分析モデルと切片だけのモデルの対数尤度を計算
Lm <- logLik(glm(single ~ male + age + edu + income, family = binomial(link = "logit")))
L0 <- logLik(glm(single ~ 1, family = binomial(link = "logit")))
Lm; L0
1-Lm[1]/L0[1] # McFadden
1-(Lm[1]-6)/L0[1] # adjusted McFadden
n <- length(single)
1-(exp(L0[1])/exp(Lm[1]))^(2/n) # Cox & Snell
(1-(exp(L0[1])/exp(Lm[1]))^(2/n))/(1-exp(L0[1])^(2/n)) # Nagelkerke
Lm <- logLik(glm(single ~ male + age + edu + income, family = binomial(link = "logit")))
L0 <- logLik(glm(single ~ 1, family = binomial(link = "logit")))
Lm; L0
1-Lm[1]/L0[1] # McFadden
1-(Lm[1]-6)/L0[1] # adjusted McFadden
n <- length(single)
1-(exp(L0[1])/exp(Lm[1]))^(2/n) # Cox & Snell
(1-(exp(L0[1])/exp(Lm[1]))^(2/n))/(1-exp(L0[1])^(2/n)) # Nagelkerke

一般化線型モデルの特殊例としての一般線型モデル
最後に,一般線型モデル(LM)が,一般化線型モデル(GLM)の特殊ケースである事を示しておこう。
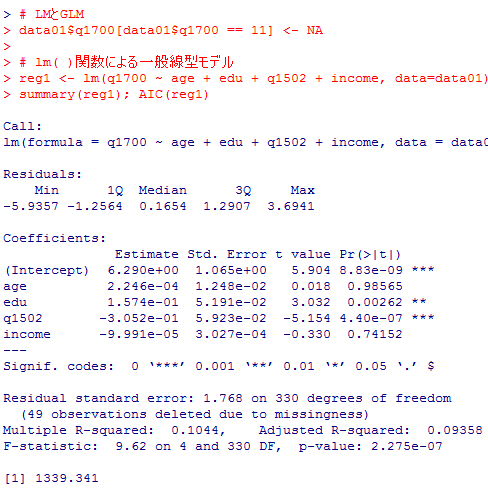
# LMとGLM
data01$q1700[data01$q1700 == 11] <- NA
# lm( )関数による一般線型モデル
reg1 <- lm(q1700 ~ age + edu + q1502 + income, data=data01)
summary(reg1); AIC(reg1)
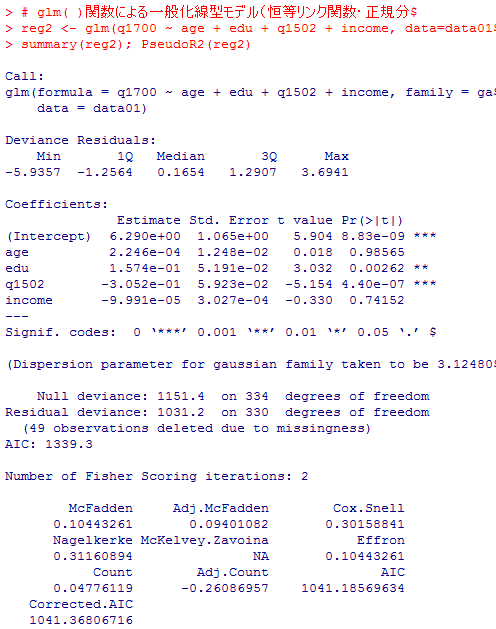
# glm( )関数による一般化線型モデル(恒等リンク関数・正規分布)
reg2 <- glm(q1700 ~ age + edu + q1502 + income, data=data01, family = gaussian(link = "identity"))
summary(reg2); PseudoR2(reg2)
data01$q1700[data01$q1700 == 11] <- NA
# lm( )関数による一般線型モデル
reg1 <- lm(q1700 ~ age + edu + q1502 + income, data=data01)
summary(reg1); AIC(reg1)
# glm( )関数による一般化線型モデル(恒等リンク関数・正規分布)
reg2 <- glm(q1700 ~ age + edu + q1502 + income, data=data01, family = gaussian(link = "identity"))
summary(reg2); PseudoR2(reg2)


偏回帰係数の推定の部分やAICは全て一致している。その他,Multiple R-squaredとMcFadden pseudo R2が一致している。
2-1 多項ロジット(Multinomial Logit Model)
nnetパッケイジを使用して,婚姻上の地位(未婚,有配偶,離死別)を性別(男性ダミー),年齢,教育年数,本人年収で説明する多項ロジット分析を行う。以下のサイトも参考にした。
AIC=Deviance + 2k,kは推定されている係数の数の10個になっている。
パラメタ推定値のz検定は以下の様にして行える。

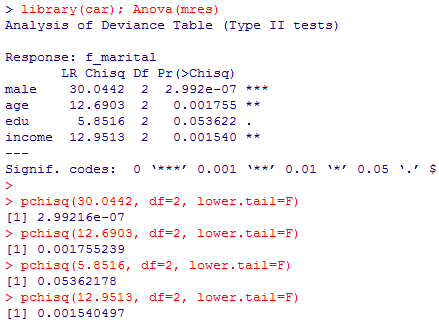
carパッケイジのAnova( )関数で,各独立変数について全体的な尤度比検定を行う。出力された情報でカイ二乗分布での確率を計算してみれば,p値が一致している事が確認出来る。
step( )関数でモデル選択を行ってみる。

以下では,まずmlogitパッケイジのmlogit( )関数による分析結果を示したのち,最初に紹介したmultinom( )関数の情報を使って同様の結果を得る方法を紹介する。
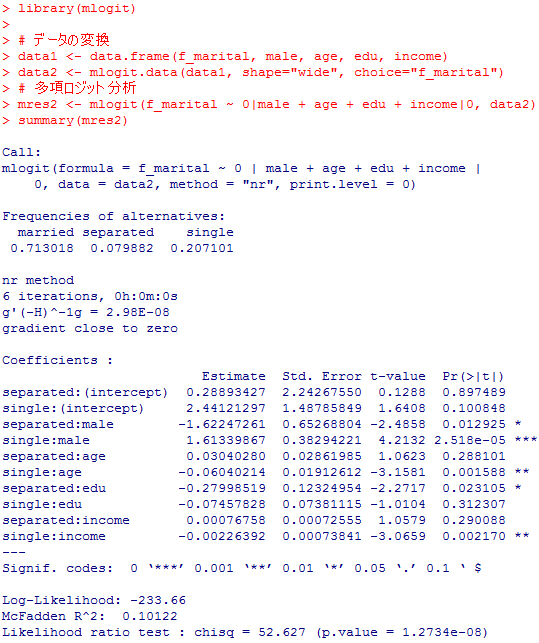
係数の推定値や標準誤差推定値はmultinom( )関数の結果と,誤差の範囲で一致していると言える。検定統計量はt-valueと表示されているが,先のz値とほぼ同一で,有意確率(両側検定)も標準正規分布を用いて計算しているようである。マクファデンの疑似決定係数や尤度比検定の結果も,multinom( )関数の結果には表示されていなかったものである。
以下では,multinom( )関数の結果を用いて,疑似決定係数や尤度比検定を行う方法である。これが出来れば,multinom( )関数の代わりに,データ形式の変換が必要なmlogit( )関数を使う理由は特にないとも言える。

mlogit( )の結果と見比べて,対数尤度の値,マクファデンの疑似決定係数の値,尤度比検定の結果も全て一致している。更に他の疑似決定係数の値も計算出来る。
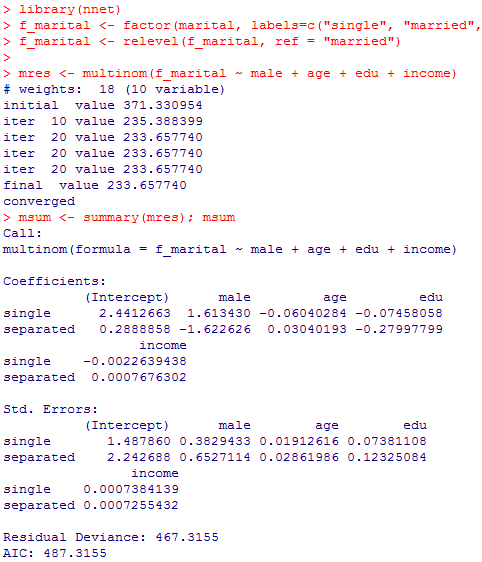
male <- c(1, 0)[data01$sex] # 男性ダミーの作成
marital <- c(2, 2, 1, 3, 3)[data01$q2100] # 婚姻上の地位: 有配偶2,未婚1,離死別3
# 完備ケース分析の準備
full <- complete.cases(data01$q2100, data01$sex, data01$age, data01$edu, data01$income)
male <- male[full]
marital <- marital[full]
age <- data01$age[full]
edu <- data01$edu[full]
income <- data01$income[full]
# 多項ロジットMultinomial Logistic Regression
# install.packages("nnet", repos="https://cran.ism.ac.jp") # 初めての時はインストールする
library(nnet)
f_marital <- factor(marital, labels=c("single", "married", "separated"))
f_marital <- relevel(f_marital, ref = "married")
mres <- multinom(f_marital ~ male + age + edu + income)
msum <- summary(mres); msum
marital <- c(2, 2, 1, 3, 3)[data01$q2100] # 婚姻上の地位: 有配偶2,未婚1,離死別3
# 完備ケース分析の準備
full <- complete.cases(data01$q2100, data01$sex, data01$age, data01$edu, data01$income)
male <- male[full]
marital <- marital[full]
age <- data01$age[full]
edu <- data01$edu[full]
income <- data01$income[full]
# 多項ロジットMultinomial Logistic Regression
# install.packages("nnet", repos="https://cran.ism.ac.jp") # 初めての時はインストールする
library(nnet)
f_marital <- factor(marital, labels=c("single", "married", "separated"))
f_marital <- relevel(f_marital, ref = "married")
mres <- multinom(f_marital ~ male + age + edu + income)
msum <- summary(mres); msum

AIC=Deviance + 2k,kは推定されている係数の数の10個になっている。
パラメタ推定値のz検定は以下の様にして行える。
names(msum)
z <- msum$coefficients/msum$standard.errors
p <- pnorm(abs(z), mean=0, sd=1, lower.tail=F)*2
z # 検定統計量
p # 有意確率
z <- msum$coefficients/msum$standard.errors
p <- pnorm(abs(z), mean=0, sd=1, lower.tail=F)*2
z # 検定統計量
p # 有意確率

carパッケイジのAnova( )関数で,各独立変数について全体的な尤度比検定を行う。出力された情報でカイ二乗分布での確率を計算してみれば,p値が一致している事が確認出来る。

step( )関数でモデル選択を行ってみる。



"nnet"のmultinom( )関数と"mlogit"のmlogit( )関数
このnnetのmultinom( )関数では,係数のz検定の結果も,疑似決定係数も出力しないのでやや不親切にも感じる。mlogitパッケイジのmlogit( )関数はもっと多くの情報を出力するので便利に思えるが,データの形式を変換してから分析を行わなければならないので却って面倒な部分もある。しかも,z検定や疑似決定係数は,multinom( )の情報を使って自分で計算する事は可能である。どちらのパッケイジ,どちらの関数の方が自分にとって簡単であるかによって判断しよう。以下では,まずmlogitパッケイジのmlogit( )関数による分析結果を示したのち,最初に紹介したmultinom( )関数の情報を使って同様の結果を得る方法を紹介する。
# install.packages("mlogit", repos="https://cran.ism.ac.jp")
library(mlogit)
# データの変換
data1 <- data.frame(f_marital, male, age, edu, income)
data2 <- mlogit.data(data1, shape="wide", choice="f_marital")
# 多項ロジット分析
mres2 <- mlogit(f_marital ~ 0|male + age + edu + income|0, data2)
summary(mres2)
library(mlogit)
# データの変換
data1 <- data.frame(f_marital, male, age, edu, income)
data2 <- mlogit.data(data1, shape="wide", choice="f_marital")
# 多項ロジット分析
mres2 <- mlogit(f_marital ~ 0|male + age + edu + income|0, data2)
summary(mres2)

係数の推定値や標準誤差推定値はmultinom( )関数の結果と,誤差の範囲で一致していると言える。検定統計量はt-valueと表示されているが,先のz値とほぼ同一で,有意確率(両側検定)も標準正規分布を用いて計算しているようである。マクファデンの疑似決定係数や尤度比検定の結果も,multinom( )関数の結果には表示されていなかったものである。
以下では,multinom( )関数の結果を用いて,疑似決定係数や尤度比検定を行う方法である。これが出来れば,multinom( )関数の代わりに,データ形式の変換が必要なmlogit( )関数を使う理由は特にないとも言える。
## multinom( )の結果から疑似決定係数
# 分析モデルと切片だけのモデルの対数尤度を計算
Lm <- logLik(multinom(f_marital ~ male + age + edu + income))
L0 <- logLik(multinom(f_marital ~ 1))
Lm; L0
1-Lm[1]/L0[1] # McFadden
n <- length(f_marital)
1-(exp(L0[1])/exp(Lm[1]))^(2/n) # Cox & Snell
(1-(exp(L0[1])/exp(Lm[1]))^(2/n))/(1-exp(L0[1])^(2/n)) # Nagelkerke
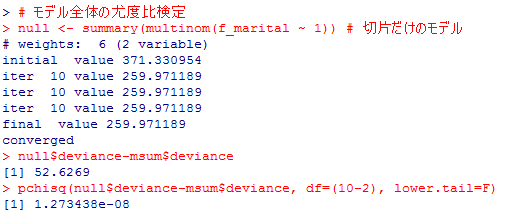
# モデル全体の尤度比検定
null <- summary(multinom(f_marital ~ 1)) # 切片だけのモデル
pchisq(null$deviance-msum$deviance, df=2*4, lower.tail=F)
# 分析モデルと切片だけのモデルの対数尤度を計算
Lm <- logLik(multinom(f_marital ~ male + age + edu + income))
L0 <- logLik(multinom(f_marital ~ 1))
Lm; L0
1-Lm[1]/L0[1] # McFadden
n <- length(f_marital)
1-(exp(L0[1])/exp(Lm[1]))^(2/n) # Cox & Snell
(1-(exp(L0[1])/exp(Lm[1]))^(2/n))/(1-exp(L0[1])^(2/n)) # Nagelkerke
# モデル全体の尤度比検定
null <- summary(multinom(f_marital ~ 1)) # 切片だけのモデル
pchisq(null$deviance-msum$deviance, df=2*4, lower.tail=F)


mlogit( )の結果と見比べて,対数尤度の値,マクファデンの疑似決定係数の値,尤度比検定の結果も全て一致している。更に他の疑似決定係数の値も計算出来る。
2-2 順序ロジット(Ordinal Logit Model)
順序ロジットについては以下のサイトも参考になる。
また,順序ロジットに限らず非常に情報量の多い解説ページが以下にある。
 太郎丸博,「離散変数の固定/ランダム効果モデル」(2017年2月26日閲覧)
まずはMASSパッケイジのpolr( )関数,次にordinalパッケイジのclm( )関数を紹介する。
太郎丸博,「離散変数の固定/ランダム効果モデル」(2017年2月26日閲覧)
まずはMASSパッケイジのpolr( )関数,次にordinalパッケイジのclm( )関数を紹介する。
本文で触れた,step( )による変数選択と,Anova( )による尤度比検定の結果,及び疑似決定係数の計算を示してみよう。
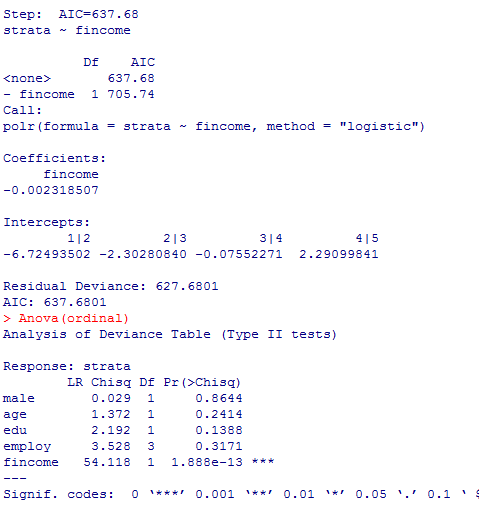
有意な変数として残るのはいずれにしても世帯年収だけであった。

世帯年収だけが有意な独立変数であったが,説明力の指標は必ずしも悪くはない様である。
出力の仕方が若干異なるが,殆ど全ての結果がほぼ一致している事が確認出来る。検定統計量がpolr( )ではt統計量,clm( )ではz統計量となっているが,結果はほぼ異ならない(但し,説明変数を増やして推定が不安定になる様な余り好ましくないモデルの場合には,分析結果に於いてt統計量とz統計量の値だけが大きく異なってくる例も見られた)。
また,順序ロジットに限らず非常に情報量の多い解説ページが以下にある。
 太郎丸博,「離散変数の固定/ランダム効果モデル」(2017年2月26日閲覧)
太郎丸博,「離散変数の固定/ランダム効果モデル」(2017年2月26日閲覧)MASSパッケイジのpolr( )関数による順序ロジット
# 5段階階層帰属意識の分布と欠損値処理
table(data01$q1501, useNA="always")
data01$q1501[data01$q1501 == 6] <- NA
# 後のことを考え,欠損値を除いておく
full <- complete.cases(data01$q1501, data01$sex, data01$age, data01$edu, data01$fincome, data01$job)
strata <- data01$q1501[full]
male <- c(1, 0)[data01$sex][full]
age <- data01$age[full]
edu <- data01$edu[full]
fincome <- data01$fincome[full]
employ <- data01$job[full]
# 名義尺度変数はfactor( )で要因型に変換する
strata <- factor(strata)
employ <- factor(employ)
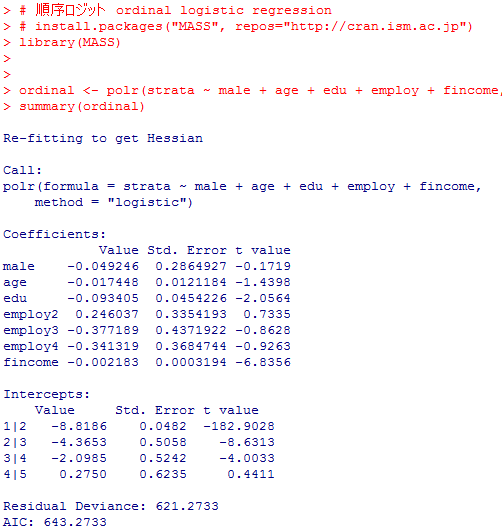
# 順序ロジット ordinal logistic regression
# install.packages("MASS", repos="http://cran.ism.ac.jp")
library(MASS)
ordinal <- polr(strata ~ male + age + edu + employ + fincome, method="logistic")
summary(ordinal)
table(data01$q1501, useNA="always")
data01$q1501[data01$q1501 == 6] <- NA
# 後のことを考え,欠損値を除いておく
full <- complete.cases(data01$q1501, data01$sex, data01$age, data01$edu, data01$fincome, data01$job)
strata <- data01$q1501[full]
male <- c(1, 0)[data01$sex][full]
age <- data01$age[full]
edu <- data01$edu[full]
fincome <- data01$fincome[full]
employ <- data01$job[full]
# 名義尺度変数はfactor( )で要因型に変換する
strata <- factor(strata)
employ <- factor(employ)
# 順序ロジット ordinal logistic regression
# install.packages("MASS", repos="http://cran.ism.ac.jp")
library(MASS)
ordinal <- polr(strata ~ male + age + edu + employ + fincome, method="logistic")
summary(ordinal)

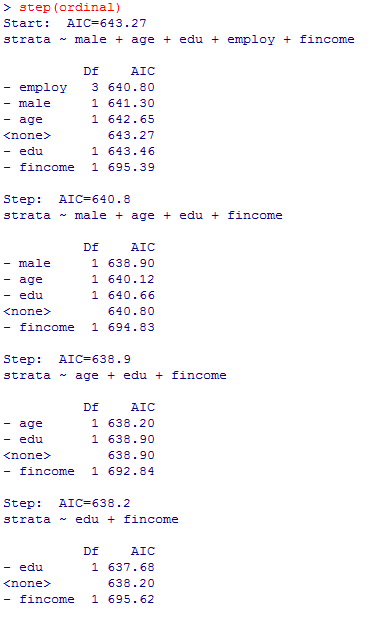
本文で触れた,step( )による変数選択と,Anova( )による尤度比検定の結果,及び疑似決定係数の計算を示してみよう。


有意な変数として残るのはいずれにしても世帯年収だけであった。
## polr( )の結果から疑似決定係数
# 分析モデルと切片だけのモデルの対数尤度を計算
Lm <- logLik(polr(strata ~ male + age + edu + employ + fincome, method="logistic"))
L0 <- logLik(polr(strata ~ 1, method="logistic"))
Lm; L0
1-Lm[1]/L0[1] # McFadden
n <- length(strata)
1-(exp(L0[1])/exp(Lm[1]))^(2/n) # Cox & Snell
(1-(exp(L0[1])/exp(Lm[1]))^(2/n))/(1-exp(L0[1])^(2/n)) # Nagelkerke
# モデル全体の尤度比検定
null <- polr(strata ~ 1, method="logistic")
null$deviance-ordinal$deviance
pchisq(null$deviance-ordinal$deviance, df=(11-4), lower.tail=F)
# 分析モデルと切片だけのモデルの対数尤度を計算
Lm <- logLik(polr(strata ~ male + age + edu + employ + fincome, method="logistic"))
L0 <- logLik(polr(strata ~ 1, method="logistic"))
Lm; L0
1-Lm[1]/L0[1] # McFadden
n <- length(strata)
1-(exp(L0[1])/exp(Lm[1]))^(2/n) # Cox & Snell
(1-(exp(L0[1])/exp(Lm[1]))^(2/n))/(1-exp(L0[1])^(2/n)) # Nagelkerke
# モデル全体の尤度比検定
null <- polr(strata ~ 1, method="logistic")
null$deviance-ordinal$deviance
pchisq(null$deviance-ordinal$deviance, df=(11-4), lower.tail=F)

世帯年収だけが有意な独立変数であったが,説明力の指標は必ずしも悪くはない様である。
ordinalパッケイジのclm( )関数による順序ロジットとの比較
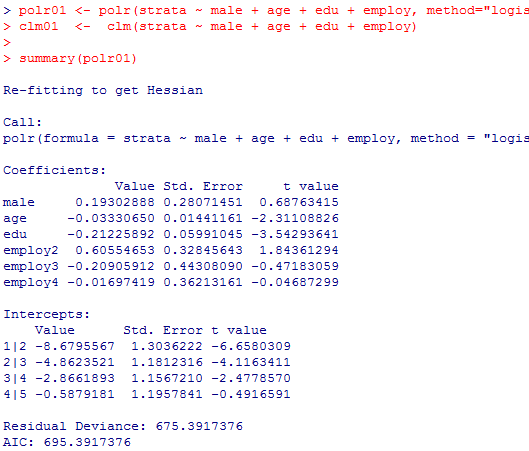
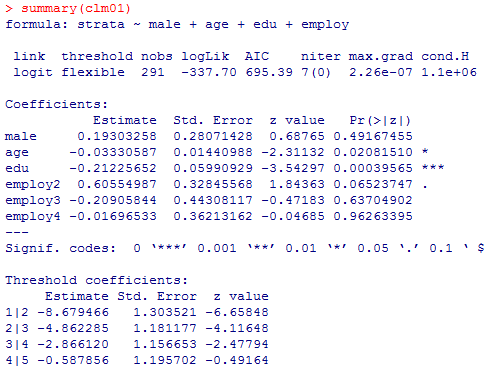
polr( )関数とclm( )関数の結果を比較しておこう。見易い様に説明変数の数を減らしておく。ordinalパッケイジをinstallしていない場合の為に,コメント行としてinstall.packages( )から書いておく。
# install.packages("ordinal", repos="http://cran.ism.ac.jp")
library(ordinal)
# 単純な同一のモデルの比較
polr01 <- polr(strata ~ male + age + edu + employ, method="logistic")
clm01 <- clm(strata ~ male + age + edu + employ)
summary(polr01)
summary(clm01)
library(ordinal)
# 単純な同一のモデルの比較
polr01 <- polr(strata ~ male + age + edu + employ, method="logistic")
clm01 <- clm(strata ~ male + age + edu + employ)
summary(polr01)
summary(clm01)


出力の仕方が若干異なるが,殆ど全ての結果がほぼ一致している事が確認出来る。検定統計量がpolr( )ではt統計量,clm( )ではz統計量となっているが,結果はほぼ異ならない(但し,説明変数を増やして推定が不安定になる様な余り好ましくないモデルの場合には,分析結果に於いてt統計量とz統計量の値だけが大きく異なってくる例も見られた)。
発展1 ログリニアモデル(log-linear model; 対数線型モデル)
本文で紹介しているログリニア・モデル(対数線型モデル)を実行してみる。

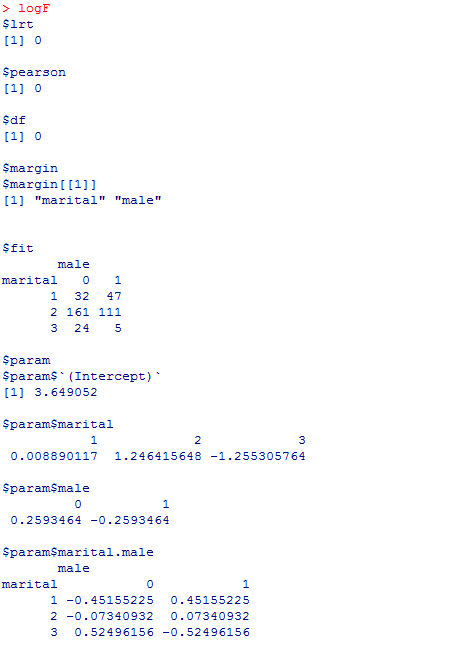
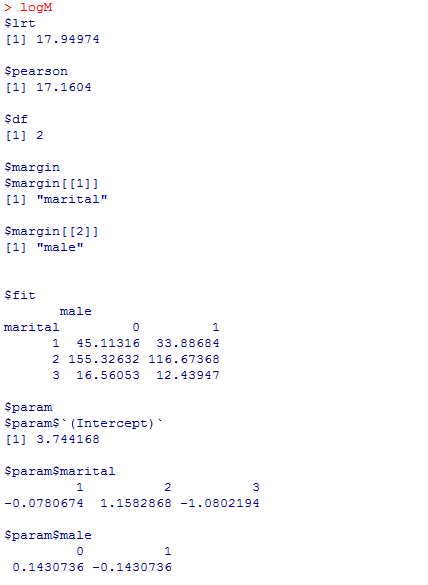
logFは飽和モデルであり, $fit(このモデルによって推定された度数)が観測度数に完全に一致している。つまり,データと観測度数の間に乖離がなく,逸脱度$lrtは0,自由度$dfも0となる。性と婚姻上の地位の関連を設定しないlogMでは,逸脱度もカイ二乗値$pearsonもある。これらの有意確率を自分で計算し,かつ元の連関表t01の独立性のカイ二乗検定の結果と比較してみよう。
pchisq( )の結果から,モデルとデータのズレはいずれにしても1%有意であり,モデルがデータにフィットしているとは言えない。$pearsonの検定結果は,クロス表のカイ二乗検定を行った結果と同じである事が確認出来る。また,logMの推定度数の表$fitはカイ二乗検定における期待度数の表と同一である。
次に,性,学歴,婚姻上の地位の3つの変数についてログリニアで分析してみる。

この飽和モデルは必然的にデータに一致するものであり,これ自体は意味はない。ここからどれだけモデルを簡潔にしても適合度が有意に低下しないかがログリニア・モデルの基本的考え方である。
まずは,3次の交互作用を除外してみる。取り敢えずモデルの逸脱度に関心があるので,param=Tとfit=Tは省略する。

逸脱度もカイ二乗統計量も有意にはならない。つまり,飽和モデルよりもズレの指標は多少悪化するが,その悪化の程度は統計的に有意ではない。飽和モデルではなくこのモデルを採用しても,データには同じ程度に適合していると考える事が出来る。
ここから更にモデルを簡略化出来るかどうか検討する。

逸脱度の検定結果,上の二つは5%水準で有意になる。つまり逸脱の程度が偶然とは思えない「悪い」モデルだと云う事である。最後のモデルは逸脱度が有意ではないので,「飽和モデルと同程度の適合度である」と云うゼロ仮説が棄却出来ず,だったらより簡潔なモデルであるlog23.13の方が優れていると考える。除外されたのは1(婚姻上の地位)と2(学歴)の関連なので,学歴によって婚姻上の地位は変わらない,と云う事を意味する。
では,更に2次の交互作用項を除外する事が出来るかどうか検討してみよう。

性別を含んだ交互作用項を除外すると,いずれにしても有意に逸脱度(適合度)が悪いするので,これ以上モデルを単純化する事は出来ない事が分かった。最終的に採用されたモデルの分析結果を詳しく確認しておこう。


尤度比やピアソンカイ二乗値,自由度は,先のloglin( )関数の結果と一致しているが,有意確率まで自動で表示してくれるので便利である。パラメタ推定値もloglin( )関数の結果と同じである。ここまではわざわざMASSパッケイジをインストールしてloglm( )を使う理由はない。
しかし,loglin( )関数の結果のオブジェクトでは,変数選択の為のstep( )関数もstepAIC( )関数も使用できないが,MASSのloglm( )関数ではこれらが使えるので,変数を削除してモデルを簡潔に出来るかどうかを検討するにはとても便利である。最初に飽和モデルを設定してstep( )にかけるところからやってみよう。

この結果を見ると,最初に3次の交互作用が除外され,次に婚姻上の地位と学歴の2次の交互作用が除外されている。それ以上は削除される交互作用項が存在しなかい事が最後に示され,最終的に採用されたモデルの尤度比検定結果が表示されている。AICなどの値は本文で表に纏めたものと一致している事を確認して欲しい。パラメタ推定値は既にloglm2の結果を表示してあるので省略する。
## 分析対象の変数の準備
male <- c(1, 0)[data01$sex] # 男性ダミーの作成
marital <- c(2, 2, 1, 3, 3)[data01$q2100] # 婚姻上の地位: 有配偶2,未婚1,離死別3
## 基本となる連関表t01(分割表,クロス表)の作成
# t02は周辺度数を付加した表,t03は列%の表
t01 <- table(marital, male); t02 <- addmargins(t01); t02
t03 <- prop.table(t01, margin=2); round(t03*100, 1)
logF <- loglin(t01, margin=list(c(1,2)), fit=T, param=T)
logM <- loglin(t01, margin=list(1,2), fit=T, param=T)
logF
male <- c(1, 0)[data01$sex] # 男性ダミーの作成
marital <- c(2, 2, 1, 3, 3)[data01$q2100] # 婚姻上の地位: 有配偶2,未婚1,離死別3
## 基本となる連関表t01(分割表,クロス表)の作成
# t02は周辺度数を付加した表,t03は列%の表
t01 <- table(marital, male); t02 <- addmargins(t01); t02
t03 <- prop.table(t01, margin=2); round(t03*100, 1)
logF <- loglin(t01, margin=list(c(1,2)), fit=T, param=T)
logM <- loglin(t01, margin=list(1,2), fit=T, param=T)
logF



logFは飽和モデルであり, $fit(このモデルによって推定された度数)が観測度数に完全に一致している。つまり,データと観測度数の間に乖離がなく,逸脱度$lrtは0,自由度$dfも0となる。性と婚姻上の地位の関連を設定しないlogMでは,逸脱度もカイ二乗値$pearsonもある。これらの有意確率を自分で計算し,かつ元の連関表t01の独立性のカイ二乗検定の結果と比較してみよう。
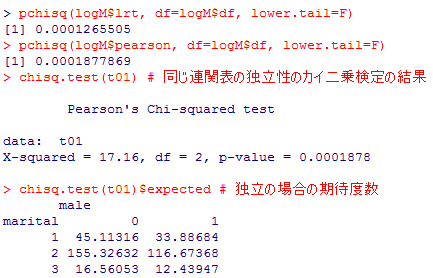
pchisq(logM$lrt, df=logM$df, lower.tail=F)
pchisq(logM$pearson, df=logM$df, lower.tail=F)
chisq.test(t01) # 同じ連関表の独立性のカイ二乗検定の結果
chisq.test(t01)$expected # 独立の場合の期待度数
pchisq(logM$pearson, df=logM$df, lower.tail=F)
chisq.test(t01) # 同じ連関表の独立性のカイ二乗検定の結果
chisq.test(t01)$expected # 独立の場合の期待度数

pchisq( )の結果から,モデルとデータのズレはいずれにしても1%有意であり,モデルがデータにフィットしているとは言えない。$pearsonの検定結果は,クロス表のカイ二乗検定を行った結果と同じである事が確認出来る。また,logMの推定度数の表$fitはカイ二乗検定における期待度数の表と同一である。
次に,性,学歴,婚姻上の地位の3つの変数についてログリニアで分析してみる。
table(data01$edu2) # 高校1,短大・高専2,四大以上3
school <- data01$edu2
tm <- table(marital, school, male); tm
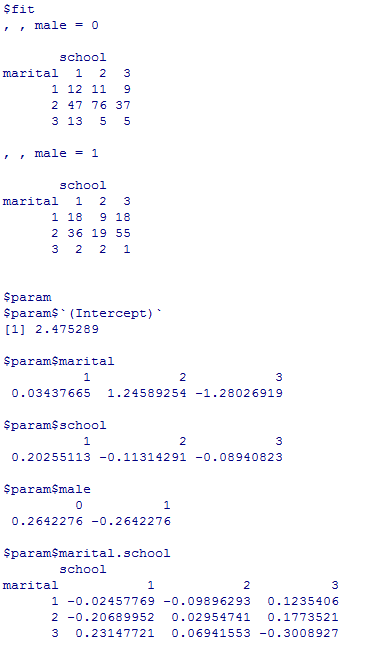
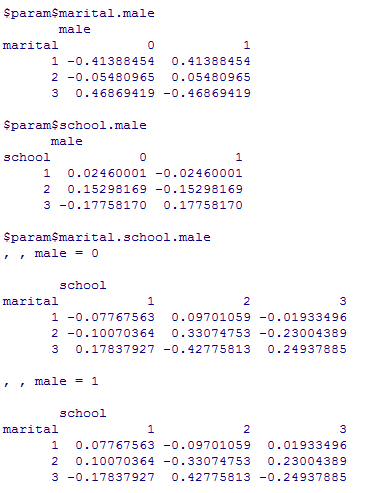
loglin(tm, margin=list(c(1, 2, 3)), fit=T, param=T) # 飽和モデル
school <- data01$edu2
tm <- table(marital, school, male); tm
loglin(tm, margin=list(c(1, 2, 3)), fit=T, param=T) # 飽和モデル



この飽和モデルは必然的にデータに一致するものであり,これ自体は意味はない。ここからどれだけモデルを簡潔にしても適合度が有意に低下しないかがログリニア・モデルの基本的考え方である。
まずは,3次の交互作用を除外してみる。取り敢えずモデルの逸脱度に関心があるので,param=Tとfit=Tは省略する。
# 2次交互作用を全て含んだモデル
log12.23.13 <- loglin(tm, margin=list(c(1, 2), c(2, 3), c(1, 3)))
log12.23.13
pchisq(log12.23.13$lrt, log12.23.13$df, lower.tail=F)
pchisq(log12.23.13$pearson, log12.23.13$df, lower.tail=F)
log12.23.13 <- loglin(tm, margin=list(c(1, 2), c(2, 3), c(1, 3)))
log12.23.13
pchisq(log12.23.13$lrt, log12.23.13$df, lower.tail=F)
pchisq(log12.23.13$pearson, log12.23.13$df, lower.tail=F)

逸脱度もカイ二乗統計量も有意にはならない。つまり,飽和モデルよりもズレの指標は多少悪化するが,その悪化の程度は統計的に有意ではない。飽和モデルではなくこのモデルを採用しても,データには同じ程度に適合していると考える事が出来る。
ここから更にモデルを簡略化出来るかどうか検討する。
# 2次交互作用を1つ除外したモデル
log12.23 <- loglin(tm, margin=list(c(1, 2), c(2, 3)))
log12.23$lrt; log12.23$df
pchisq(log12.23$lrt, log12.23$df, lower.tail=F)
log12.13 <- loglin(tm, margin=list(c(1, 2), c(1, 3)))
log12.13$lrt; log12.13$df
pchisq(log12.13$lrt, log12.13$df, lower.tail=F)
log23.13 <- loglin(tm, margin=list(c(2, 3), c(1, 3)))
log23.13$lrt; log23.13$df
pchisq(log23.13$lrt, log23.13$df, lower.tail=F)
log12.23 <- loglin(tm, margin=list(c(1, 2), c(2, 3)))
log12.23$lrt; log12.23$df
pchisq(log12.23$lrt, log12.23$df, lower.tail=F)
log12.13 <- loglin(tm, margin=list(c(1, 2), c(1, 3)))
log12.13$lrt; log12.13$df
pchisq(log12.13$lrt, log12.13$df, lower.tail=F)
log23.13 <- loglin(tm, margin=list(c(2, 3), c(1, 3)))
log23.13$lrt; log23.13$df
pchisq(log23.13$lrt, log23.13$df, lower.tail=F)

逸脱度の検定結果,上の二つは5%水準で有意になる。つまり逸脱の程度が偶然とは思えない「悪い」モデルだと云う事である。最後のモデルは逸脱度が有意ではないので,「飽和モデルと同程度の適合度である」と云うゼロ仮説が棄却出来ず,だったらより簡潔なモデルであるlog23.13の方が優れていると考える。除外されたのは1(婚姻上の地位)と2(学歴)の関連なので,学歴によって婚姻上の地位は変わらない,と云う事を意味する。
では,更に2次の交互作用項を除外する事が出来るかどうか検討してみよう。
# 2次交互作用をもう一つ除外したモデル
log23 <- loglin(tm, margin=list(c(2, 3)))
log23$lrt; log23$df
pchisq(log23$lrt, log23$df, lower.tail=F)
log13 <- loglin(tm, margin=list(c(1, 3)))
log13$lrt; log13$df
pchisq(log13$lrt, log13$df, lower.tail=F)
log23 <- loglin(tm, margin=list(c(2, 3)))
log23$lrt; log23$df
pchisq(log23$lrt, log23$df, lower.tail=F)
log13 <- loglin(tm, margin=list(c(1, 3)))
log13$lrt; log13$df
pchisq(log13$lrt, log13$df, lower.tail=F)

性別を含んだ交互作用項を除外すると,いずれにしても有意に逸脱度(適合度)が悪いするので,これ以上モデルを単純化する事は出来ない事が分かった。最終的に採用されたモデルの分析結果を詳しく確認しておこう。


"MASS"のloglm( )関数
次は,MASSパッケイジ中のloglm( )関数でログリニアモデルの分析をしてみよう。まずは上で最終的に採用されたモデルを分析してみる。
library(MASS)
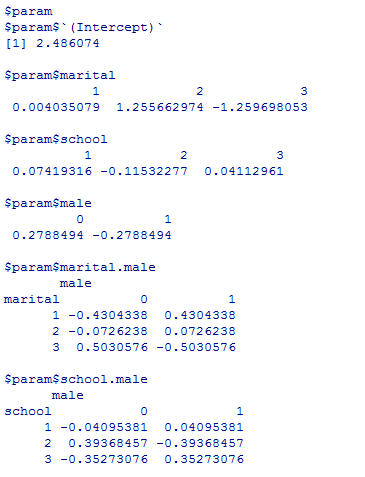
loglm2 <- loglm(~ marital * male + school * male, data=tm)
loglm2; extractAIC(loglm2)
loglm2$param # パラメタ推定値を表示
loglm2 <- loglm(~ marital * male + school * male, data=tm)
loglm2; extractAIC(loglm2)
loglm2$param # パラメタ推定値を表示

尤度比やピアソンカイ二乗値,自由度は,先のloglin( )関数の結果と一致しているが,有意確率まで自動で表示してくれるので便利である。パラメタ推定値もloglin( )関数の結果と同じである。ここまではわざわざMASSパッケイジをインストールしてloglm( )を使う理由はない。
しかし,loglin( )関数の結果のオブジェクトでは,変数選択の為のstep( )関数もstepAIC( )関数も使用できないが,MASSのloglm( )関数ではこれらが使えるので,変数を削除してモデルを簡潔に出来るかどうかを検討するにはとても便利である。最初に飽和モデルを設定してstep( )にかけるところからやってみよう。
loglmF <- loglm(~ marital * male * school, data=tm) # 飽和モデル
step(loglmF)
stepAIC(loglmF) # こちらでも全く同じ
step(loglmF)
stepAIC(loglmF) # こちらでも全く同じ

この結果を見ると,最初に3次の交互作用が除外され,次に婚姻上の地位と学歴の2次の交互作用が除外されている。それ以上は削除される交互作用項が存在しなかい事が最後に示され,最終的に採用されたモデルの尤度比検定結果が表示されている。AICなどの値は本文で表に纏めたものと一致している事を確認して欲しい。パラメタ推定値は既にloglm2の結果を表示してあるので省略する。
Copyright (C) 2016-2017 SUGINO Isamu All Rights Reserved. design by tempnate

