杉野 勇 (SUGINO Isamu) お茶の水女子大学・人間発達科学専攻・応用社会学コース担当
『入門・社会統計学』サポートウェブ |
|
 第9章 重回帰分析(?)(MRA)
第9章 重回帰分析(?)(MRA)
1-1 偏回帰係数(partial regression coefficient)のt検定と区間推定
本文の,幸福度を,年齢,教育年数,階層帰属意識,世帯年収で説明する重回帰分析を行い(reg0901),その結果を表示する。データフレイム名はdata01としているので注意せよ。

偏回帰係数は,年齢と教育年数は全く有意ではなく,階層帰属意識(q1502)と世帯収入は1%水準で有意である。
標本偏回帰係数(Estimate)をその標準誤差(Std. Error)で割った値がt統計量(t value)であり,その両側検定の有意確率が(Pr(>|t|))である。オブジェクトに格納された情報を使って,この事を以下の様に確認してみよう。

それぞれの計算結果が何処に対応しているのかよく確認しよう。因みに,この自由度(df=287)のt分布の95%区間の限界値はqt(.025, df=reg0901$df.residual, lower.tail=F)もしくはqt(.975, df=reg0901$df.residual)で求めることができ,1.968264である。

95%信頼区間,90%信頼区間をconfint( )関数で求めた後,90%信頼区間の上限と下限をオブジェクトreg0901やsum0901の情報を使って求めてみる。結果がきちんと一致している事を確認して,信頼区間の関数がどの様な計算をしているのかなどについて理解を深めよう。

 この例題をベイズ統計学的手法で計算した例を,このサポートウェブの〔付録〕2-2に示しています。
この例題をベイズ統計学的手法で計算した例を,このサポートウェブの〔付録〕2-2に示しています。
## 幸福度の欠損値処理
data01$q1700[data01$q1700 == 11] <- NA
reg0901 <- lm(q1700 ~ age + edu + q1502 + fincome, data01)
sum0901 <- summary(reg0901)
sum0901
data01$q1700[data01$q1700 == 11] <- NA
reg0901 <- lm(q1700 ~ age + edu + q1502 + fincome, data01)
sum0901 <- summary(reg0901)
sum0901

偏回帰係数は,年齢と教育年数は全く有意ではなく,階層帰属意識(q1502)と世帯収入は1%水準で有意である。
標本偏回帰係数(Estimate)をその標準誤差(Std. Error)で割った値がt統計量(t value)であり,その両側検定の有意確率が(Pr(>|t|))である。オブジェクトに格納された情報を使って,この事を以下の様に確認してみよう。
names(reg0901) # lm( )関数の結果
names(sum0901) # summary( )関数の結果
coef <- sum0901$coefficients; coef # summary( )関数の一部
coef[,1]/coef[,2] # 偏回帰係数÷標準誤差=t統計量
reg0901$df.residual # 偏回帰係数のt検定の自由度
# 両側検定の有意確率なので最後に2倍している。
pt(abs(coef[,1]/coef[,2]), df=reg0901$df.residual, lower.tail=F)*2
names(sum0901) # summary( )関数の結果
coef <- sum0901$coefficients; coef # summary( )関数の一部
coef[,1]/coef[,2] # 偏回帰係数÷標準誤差=t統計量
reg0901$df.residual # 偏回帰係数のt検定の自由度
# 両側検定の有意確率なので最後に2倍している。
pt(abs(coef[,1]/coef[,2]), df=reg0901$df.residual, lower.tail=F)*2

それぞれの計算結果が何処に対応しているのかよく確認しよう。因みに,この自由度(df=287)のt分布の95%区間の限界値はqt(.025, df=reg0901$df.residual, lower.tail=F)もしくはqt(.975, df=reg0901$df.residual)で求めることができ,1.968264である。

95%信頼区間,90%信頼区間をconfint( )関数で求めた後,90%信頼区間の上限と下限をオブジェクトreg0901やsum0901の情報を使って求めてみる。結果がきちんと一致している事を確認して,信頼区間の関数がどの様な計算をしているのかなどについて理解を深めよう。
confint(reg0901, level=.95)
confint(reg0901, level=.90)
# 90%信頼区間の下限を計算
coef[,1] - qt(.05, df=reg0901$df.residual, lower.tail=F)*coef[,2]
# 90%信頼区間の上限を計算
coef[,1] + qt(.05, df=reg0901$df.residual, lower.tail=F)*coef[,2]
confint(reg0901, level=.90)
# 90%信頼区間の下限を計算
coef[,1] - qt(.05, df=reg0901$df.residual, lower.tail=F)*coef[,2]
# 90%信頼区間の上限を計算
coef[,1] + qt(.05, df=reg0901$df.residual, lower.tail=F)*coef[,2]

 この例題をベイズ統計学的手法で計算した例を,このサポートウェブの〔付録〕2-2に示しています。
この例題をベイズ統計学的手法で計算した例を,このサポートウェブの〔付録〕2-2に示しています。
1-2 分散説明率R2の増分のF検定
分散分析表を作成する為に,anova( )関数を使用する。また,独立変数の平方和の合計を求めるために少し工夫している。
F統計量と分散説明率の関係を数式で本文よりも丁寧に示しておこう(クリックしてPDFに)。

Rでの計算の確認は以下の通りである。

偏回帰係数のt検定と(部分)モデルのF検定の同等性については,本文では簡単な説明しか出来なかったので,ここで少し詳しく説明しておこう。

モデルSからモデルLへは分散説明率の増分は.0416(4.16%ポイント)であり,自由度の増加は1である。

モデルLとモデルSの分散説明率の増加分から計算したF統計量であるF0は,モデルLの独立変数x4のt統計量の二乗と一致している。最後のF0のF検定の有意確率もモデルLの独立変数x4のt検定の有意確率と一致している。
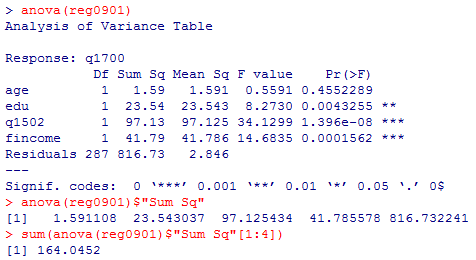
anova(reg0901)
anova(reg0901)$"Sum Sq"
sum(anova(reg0901)$"Sum Sq"[1:4])
anova(reg0901)$"Sum Sq"
sum(anova(reg0901)$"Sum Sq"[1:4])

F統計量と分散説明率の関係を数式で本文よりも丁寧に示しておこう(クリックしてPDFに)。

Rでの計算の確認は以下の通りである。
sum0901$r.squared # 分散説明率
sum0901$fstatistic[2] # F統計量の分子自由度
sum0901$fstatistic[3] # F統計量の分母自由度
sum0901$fstatistic[1] # F統計量
# F統計量とR2の関係式から計算
sum0901$r.squared/sum0901$fstatistic[2]/((1-sum0901$r.squared)/sum0901$fstatistic[3])
sum0901$fstatistic[2] # F統計量の分子自由度
sum0901$fstatistic[3] # F統計量の分母自由度
sum0901$fstatistic[1] # F統計量
# F統計量とR2の関係式から計算
sum0901$r.squared/sum0901$fstatistic[2]/((1-sum0901$r.squared)/sum0901$fstatistic[3])

偏回帰係数のt検定と(部分)モデルのF検定の同等性については,本文では簡単な説明しか出来なかったので,ここで少し詳しく説明しておこう。
# 大きい方のモデルですべての変数が有効であるケースに限定
TorF <- complete.cases(data01$q1700, data01$age, data01$edu, data01$q1502, data01$fincome)
y <- data01$q1700[TorF]
x1 <- data01$age[TorF]
x2 <- data01$edu[TorF]
x3 <- data01$q1502[TorF]
x4 <- data01$fincome[TorF]
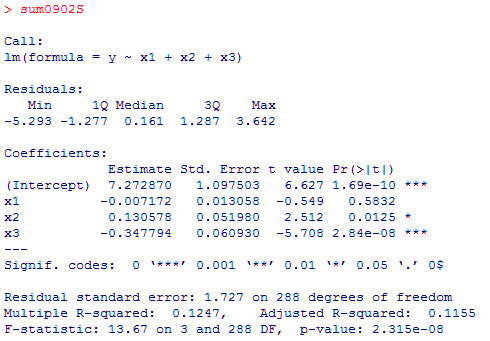
sum0902L <- summary(reg0902L <- lm(y ~ x1 + x2 + x3 + x4)) # モデルL
sum0902S <- summary(reg0902S <- lm(y ~ x1 + x2 + x3)) # モデルS
sum0902L
sum0902S
TorF <- complete.cases(data01$q1700, data01$age, data01$edu, data01$q1502, data01$fincome)
y <- data01$q1700[TorF]
x1 <- data01$age[TorF]
x2 <- data01$edu[TorF]
x3 <- data01$q1502[TorF]
x4 <- data01$fincome[TorF]
sum0902L <- summary(reg0902L <- lm(y ~ x1 + x2 + x3 + x4)) # モデルL
sum0902S <- summary(reg0902S <- lm(y ~ x1 + x2 + x3)) # モデルS
sum0902L
sum0902S


モデルSからモデルLへは分散説明率の増分は.0416(4.16%ポイント)であり,自由度の増加は1である。
# 分散説明率の増分についての,F統計量の計算
F0 <- (sum0902L$r.squared - sum0902S$r.squared)/((1-sum0902L$r.squared)/sum0902L$df[2]) # F統計量
F0
sum0902L$coefficients[5,3] # モデルLにおけるx4の偏回帰係数のt統計量
sum0902L$coefficients[5,3]^2 # モデルLにおけるx4の偏回帰係数のt統計量の2乗
# F統計量F0に対応する有意確率の計算
pf(F0, 1, 287, lower.tail=F)
F0 <- (sum0902L$r.squared - sum0902S$r.squared)/((1-sum0902L$r.squared)/sum0902L$df[2]) # F統計量
F0
sum0902L$coefficients[5,3] # モデルLにおけるx4の偏回帰係数のt統計量
sum0902L$coefficients[5,3]^2 # モデルLにおけるx4の偏回帰係数のt統計量の2乗
# F統計量F0に対応する有意確率の計算
pf(F0, 1, 287, lower.tail=F)

モデルLとモデルSの分散説明率の増加分から計算したF統計量であるF0は,モデルLの独立変数x4のt統計量の二乗と一致している。最後のF0のF検定の有意確率もモデルLの独立変数x4のt検定の有意確率と一致している。
1-3 標準化偏回帰係数(standardized partial regression coefficient)
全ての変数を完備ケース分析用に準備した上で標準化し,重回帰分析を行う。そして,標準化偏回帰係数と独立変数・従属変数の標準偏差から非標準化係数を計算し,1-2のモデルLの結果と一致する事を確認する。最後に,標準化係数の信頼区間を求めておく。(出力結果では準備の部分は省略した。)


階層帰属意識x3と世帯年収x4の標準化係数の絶対値は階層帰属意識の方がやや大きかった。信頼区間(の絶対値)を見ても階層帰属意識の方が下限値も上限値も大きいが,しかし信頼区間はかなり重なっており,母集団に於いてはx4の効果の方が大きい事もあり得る。
# 完備ケース分析の準備
TorF <- complete.cases(data01$q1700, data01$age, data01$edu, data01$q1502, data01$fincome)
y <- data01$q1700[TorF]
x1 <- data01$age[TorF]
x2 <- data01$edu[TorF]
x3 <- data01$q1502[TorF]
x4 <- data01$fincome[TorF]
# 全ての変数をscale( )で標準化して重回帰分析
sum0903 <- summary(reg0903 <- lm(scale(y) ~ scale(x1) + scale(x2) + scale(x3) + scale(x4)))
sum0903
reg0903$coefficients[5] # 世帯年収x4の標準化偏回帰係数
sd(y)/sd(x4)*reg0903$coefficients[5] # 標準化係数と標準偏差から非標準化係数を計算
reg0902L$coefficients[5] # 世帯年収x4の非標準化係数(1-2より)
confint(reg0903, level=.95) # 標準化係数の信頼区間
TorF <- complete.cases(data01$q1700, data01$age, data01$edu, data01$q1502, data01$fincome)
y <- data01$q1700[TorF]
x1 <- data01$age[TorF]
x2 <- data01$edu[TorF]
x3 <- data01$q1502[TorF]
x4 <- data01$fincome[TorF]
# 全ての変数をscale( )で標準化して重回帰分析
sum0903 <- summary(reg0903 <- lm(scale(y) ~ scale(x1) + scale(x2) + scale(x3) + scale(x4)))
sum0903
reg0903$coefficients[5] # 世帯年収x4の標準化偏回帰係数
sd(y)/sd(x4)*reg0903$coefficients[5] # 標準化係数と標準偏差から非標準化係数を計算
reg0902L$coefficients[5] # 世帯年収x4の非標準化係数(1-2より)
confint(reg0903, level=.95) # 標準化係数の信頼区間


階層帰属意識x3と世帯年収x4の標準化係数の絶対値は階層帰属意識の方がやや大きかった。信頼区間(の絶対値)を見ても階層帰属意識の方が下限値も上限値も大きいが,しかし信頼区間はかなり重なっており,母集団に於いてはx4の効果の方が大きい事もあり得る。
1-4 分析結果の提示方法
今までの分析結果からまずは,本文の様な,重回帰分析の結果表を作成する為に必要な情報を出力する。

次に,複数のモデルの結果を比較する表の一例を作成してみよう。同じデータセットで複数のモデルの優劣を判断する場合,分析に使用されるケースを同一にしておくのが良い。特に完備ケース分析の場合,それぞれのモデルで有効ケースが大きく異なってしまわないように注意すべきである。
表に整理すべき情報は分析によって異なるかも知れない。非標準化偏回帰係数と標準化係数のいずれを表記すべきか,標準誤差は必要かそれとも有意水準を記すだけで十分かなど,迷う点もあるかも知れない。以下の例では,それぞれの独立変数が従属変数に影響しているかどうか,独立変数間でどれが影響力が大きいか,などに関心があると想定して,標準化係数と有意水準のみを表に纏めた(標準誤差,信頼区間は省略した)。

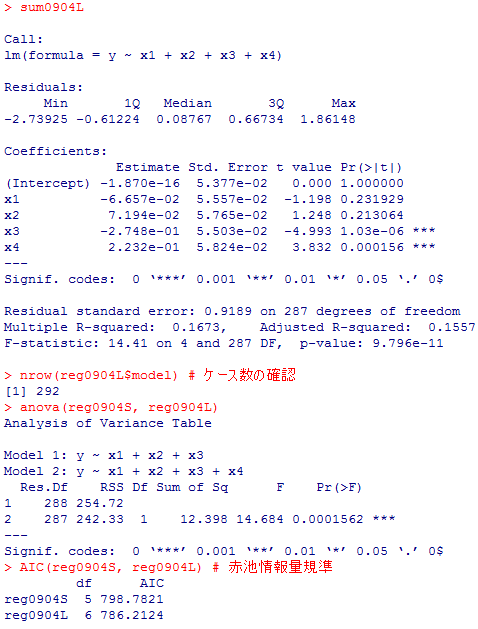
AICは,「予測の悪さ」の指標なので,小さい方が良いモデルである。なお,この場合はモデルLにおける世帯年収のt検定と,二つのモデルの差のF検定は同値である。世帯年収を追加投入したところ,世帯収入は高度に有意となり,モデルSでは5%水準で有意であった教育年数がモデルLでは有意ではなくなった。教育年数が幸福度にわずかに影響していると見えたのは実は世帯年収の効果が,世帯年収と或程度関連のある教育年数の効果として表れてしまっていただけであると考えられる。
sum0902L # 重回帰分析(非標準化解)の結果
round(sum0902L$coefficients[, c(1, 2, 4)], 4) # 数値の小数桁数を指定
round(sum0903$coefficients[, c(1, 4)], 4) # 標準化係数
length(y) # ケース数
round(sum0902L$coefficients[, c(1, 2, 4)], 4) # 数値の小数桁数を指定
round(sum0903$coefficients[, c(1, 4)], 4) # 標準化係数
length(y) # ケース数

次に,複数のモデルの結果を比較する表の一例を作成してみよう。同じデータセットで複数のモデルの優劣を判断する場合,分析に使用されるケースを同一にしておくのが良い。特に完備ケース分析の場合,それぞれのモデルで有効ケースが大きく異なってしまわないように注意すべきである。
表に整理すべき情報は分析によって異なるかも知れない。非標準化偏回帰係数と標準化係数のいずれを表記すべきか,標準誤差は必要かそれとも有意水準を記すだけで十分かなど,迷う点もあるかも知れない。以下の例では,それぞれの独立変数が従属変数に影響しているかどうか,独立変数間でどれが影響力が大きいか,などに関心があると想定して,標準化係数と有意水準のみを表に纏めた(標準誤差,信頼区間は省略した)。
# 完備ケース分析&標準化の準備
TorF <- complete.cases(data01$q1700, data01$age, data01$edu, data01$q1502, data01$fincome)
y <- scale(data01$q1700[TorF])
x1 <- scale(data01$age[TorF])
x2 <- scale(data01$edu[TorF])
x3 <- scale(data01$q1502[TorF])
x4 <- scale(data01$fincome[TorF])
sum0904S <- summary(reg0904S <- lm(y ~ x1 + x2 + x3))
sum0904L <- summary(reg0904L <- lm(y ~ x1 + x2 + x3 +x4))
sum0904S
nrow(reg0904S$model) # ケース数の確認
sum0904L
nrow(reg0904L$model) # ケース数の確認
anova(reg0904S, reg0904L)
AIC(reg0904S, reg0904L) # 赤池情報量規準
TorF <- complete.cases(data01$q1700, data01$age, data01$edu, data01$q1502, data01$fincome)
y <- scale(data01$q1700[TorF])
x1 <- scale(data01$age[TorF])
x2 <- scale(data01$edu[TorF])
x3 <- scale(data01$q1502[TorF])
x4 <- scale(data01$fincome[TorF])
sum0904S <- summary(reg0904S <- lm(y ~ x1 + x2 + x3))
sum0904L <- summary(reg0904L <- lm(y ~ x1 + x2 + x3 +x4))
sum0904S
nrow(reg0904S$model) # ケース数の確認
sum0904L
nrow(reg0904L$model) # ケース数の確認
anova(reg0904S, reg0904L)
AIC(reg0904S, reg0904L) # 赤池情報量規準


| 従属変数: 幸福度 | ||||
| モデルS | モデルL | |||
| 変数 | 標準化係数 | 有意水準 | 標準化係数 | 有意水準 |
| 年齢 | -.031 | -.067 | ||
| 教育年数 | .141 | * | .072 | |
| 階層帰属意識 | -.316 | *** | -.275 | *** |
| 世帯収入 | --- | .223 | *** | |
| R2 | .125 | .167 | ||
| 調整済みR2 | .116 | .156 | ||
| AIC | 798.78 | 786.21 | ||
| ΔR2 | .0426*** | |||
| ケース数 | 292 | |||
1-5 自由度調整済み分散説明率(Adjusted R-squared)
自由度調整済み決定係数(分散説明率)については,本文の説明をもう少し詳しくPDにて説明している。

これまでの分析結果例でも,自由度調整済み分散説明率が無調整説明率よりも必ず小さな値になっている事が確認出来るだろう。
上の1-4の重回帰分析の結果表の情報から自由度調整済み分散説明率を計算して確認してみる。

無調整のR-squaredが同じであれば,独立変数の個数pが多いほど調整済みR-squaredは小さくなる。式をよく見て理解しよう。

これまでの分析結果例でも,自由度調整済み分散説明率が無調整説明率よりも必ず小さな値になっている事が確認出来るだろう。
上の1-4の重回帰分析の結果表の情報から自由度調整済み分散説明率を計算して確認してみる。

無調整のR-squaredが同じであれば,独立変数の個数pが多いほど調整済みR-squaredは小さくなる。式をよく見て理解しよう。
発展1 1要因分散分析とダミー変数を用いた重回帰分析
第7章発展1では,2群の母平均の差のt検定と1要因分散分析が同値である事を,第8章発展1では,2群の母平均の差のt検定と単回帰分析が同一である事を示した。ここから,要因(独立変数)が2カテゴリの場合には,1要因分散分析と単回帰モデルも同値である事が分かる。本章の発展では,要因(独立変数)が3カテゴリ以上の場合に,一要因分散分析と(複数のダミー変数を用いた)重回帰分析が,同じ一般線型モデル(一般線形モデル)として同値である事を分析例で確認する。
まずはダミー変数の作成方法を紹介しよう。本文では省略したが,最も初歩的な方法だと(例えば)次の様に作る事が出来る。これは殆ど何の工夫もしていない。

本文で紹介したものはこれより少し工夫を施している。上と比べる為にそれぞれD2, D3, D4としよう。

第7章の分散分析の結果を再確認しておく。
これを,ダミー変数重回帰で再現してみよう。後の事を考えて,分析結果を一つ一つオブジェクトに格納しながら進めている。
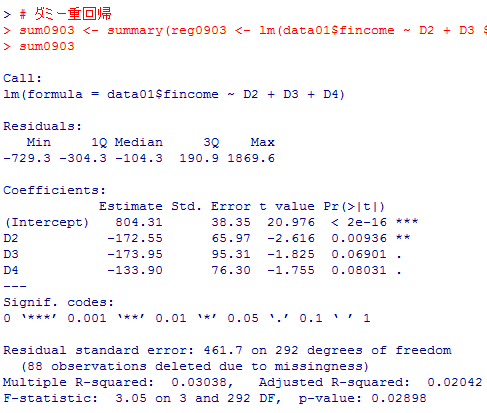
最下行のF検定の結果は分散分析の結果と一致している。定数項は804.31(万円)となっているが,これが参照カテゴリである正規雇用者の世帯年収の平均と一致し,非正規雇用ダミーd2の偏回帰係数は,非正規雇用の平均631.8と正規雇用の平均804.3との差を示している。
全てのカテゴリの平均を,分析結果を利用して計算・表示しよう。

重回帰分析の結果における,各ダミー変数の偏回帰係数のt検定の部分が,有意水準無調整の多重比較(つまり通常の2群でのt検定)に一致する事も以下の様に確認しよう。
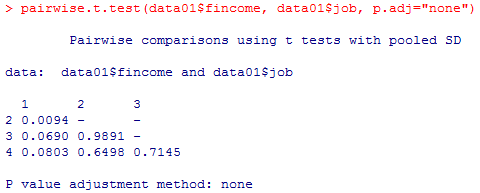
有意確率の小数の表示形式が異なるので分かりにくいかも知れないが,この多重比較の表のうち1列目(つまりカテゴリ1と他のカテゴリの比較の検定の有意確率)の数値は,重回帰分析のCoefficientsの"Pr(>|t|)"の列の結果と一致している。つまり,複数のダミー変数の偏回帰係数のt検定は,単純に二群ごとの平均値の比較のt検定を行っている事と同じなのである。異なる点は,通常の多重比較は全てのカテゴリ間の平均値差を検定するのに対して,ダミー変数重回帰では参照カテゴリと他のカテゴリとの平均値差の検定しか行わない点である。例えば上の重回帰例では,非正規と自営の平均値差の有意確率は計算されない。ここからも,どのカテゴリを参照カテゴリとすべきかが重要である事が分かる。
まずは,multcompパッケイジを新たにインストールするところから始める(出力結果は省略)。

先頭のカテゴリとそれ以外のカテゴリの比較だけが検定されている事が読み取れる。有意確率は,偏回帰係数のt検定や無調整のカテゴリ間t検定の有意確率よりも3倍近く高くなっている事が分かる。これが,検定の多重性を調整した結果である。
confint( )関数を使って,平均値差の信頼区間の出力も可能である。95%信頼区間が,有意水準5%の仮説検定の結果と対応する事はもう理解出来ただろうか。
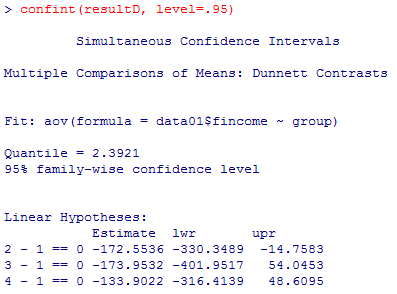
最後に,独立変数にカテゴリカル変数を指定した線型モデルlm( )の結果がダミー変数重回帰の結果と完全に一致する事を示しておこう。この様にして,同じ事を様々な方法で実行してみる事を通して,それぞれの分析手法についての理解を深めていけると良い。

まずはダミー変数の作成方法を紹介しよう。本文では省略したが,最も初歩的な方法だと(例えば)次の様に作る事が出来る。これは殆ど何の工夫もしていない。
# ダミー変数の初期化。代入するものはdata01$jobでなくても構わない。
d2 <- d3 <- d4 <- data01$job
d2[data01$job == 1] <- 0; d3[data01$job == 1] <- 0; d4[data01$job == 1] <- 0
d2[data01$job == 2] <- 1; d3[data01$job == 2] <- 0; d4[data01$job == 2] <- 0
d2[data01$job == 3] <- 0; d3[data01$job == 3] <- 1; d4[data01$job == 3] <- 0
d2[data01$job == 4] <- 0; d3[data01$job == 4] <- 0; d4[data01$job == 4] <- 1
table("job"=data01$job, d2, useNA="always") # 意図通りに正しくダミー変数が作成出来たか確認
table("job"=data01$job, d3, useNA="always")
table("job"=data01$job, d4, useNA="always")
d2 <- d3 <- d4 <- data01$job
d2[data01$job == 1] <- 0; d3[data01$job == 1] <- 0; d4[data01$job == 1] <- 0
d2[data01$job == 2] <- 1; d3[data01$job == 2] <- 0; d4[data01$job == 2] <- 0
d2[data01$job == 3] <- 0; d3[data01$job == 3] <- 1; d4[data01$job == 3] <- 0
d2[data01$job == 4] <- 0; d3[data01$job == 4] <- 0; d4[data01$job == 4] <- 1
table("job"=data01$job, d2, useNA="always") # 意図通りに正しくダミー変数が作成出来たか確認
table("job"=data01$job, d3, useNA="always")
table("job"=data01$job, d4, useNA="always")

本文で紹介したものはこれより少し工夫を施している。上と比べる為にそれぞれD2, D3, D4としよう。
x1 <- c(0, 1, 0, 0) # 非正規ダミー用ヴェクトル
x2 <- c(0, 0, 1, 0) # 自営ダミー用ヴェクトル
x3 <- c(0, 0, 0, 1) # 無職ダミー用ヴェクトル
D2 <- x1[data01$job]; D3 <- x2[data01$job]; D4 <- x3[data01$job]
table(D2, d2, useNA="always") # 上のダミー変数と同一かどうか確認
table(D3, d3, useNA="always")
table(D4, d4, useNA="always")
x2 <- c(0, 0, 1, 0) # 自営ダミー用ヴェクトル
x3 <- c(0, 0, 0, 1) # 無職ダミー用ヴェクトル
D2 <- x1[data01$job]; D3 <- x2[data01$job]; D4 <- x3[data01$job]
table(D2, d2, useNA="always") # 上のダミー変数と同一かどうか確認
table(D3, d3, useNA="always")
table(D4, d4, useNA="always")

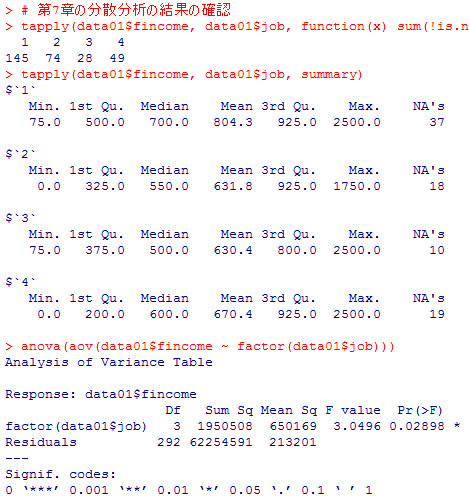
第7章の分散分析の結果を再確認しておく。
# 第7章の分散分析の結果の確認
tapply(data01$fincome, data01$job, function(x) sum(!is.na(x)))
tapply(data01$fincome, data01$job, summary)
anova(aov(data01$fincome ~ factor(data01$job)))
tapply(data01$fincome, data01$job, function(x) sum(!is.na(x)))
tapply(data01$fincome, data01$job, summary)
anova(aov(data01$fincome ~ factor(data01$job)))

これを,ダミー変数重回帰で再現してみよう。後の事を考えて,分析結果を一つ一つオブジェクトに格納しながら進めている。
# ダミー重回帰
sum0903 <- summary(reg0903 <- lm(data01$fincome ~ D2 + D3 + D4))
sum0903
sum0903 <- summary(reg0903 <- lm(data01$fincome ~ D2 + D3 + D4))
sum0903

最下行のF検定の結果は分散分析の結果と一致している。定数項は804.31(万円)となっているが,これが参照カテゴリである正規雇用者の世帯年収の平均と一致し,非正規雇用ダミーd2の偏回帰係数は,非正規雇用の平均631.8と正規雇用の平均804.3との差を示している。
全てのカテゴリの平均を,分析結果を利用して計算・表示しよう。
# 各カテゴリの平均を計算
names(sum0903)
sum0903$coefficients
sum0903$coefficients[c(1, 2), 1] # これを加算すれば非正規雇用の平均になる
sum(sum0903$coefficients[c(1, 2), 1])
sum(sum0903$coefficients[c(1, 3), 1]) # 自営の平均
sum(sum0903$coefficients[c(1, 4), 1]) # 無職の平均
names(sum0903)
sum0903$coefficients
sum0903$coefficients[c(1, 2), 1] # これを加算すれば非正規雇用の平均になる
sum(sum0903$coefficients[c(1, 2), 1])
sum(sum0903$coefficients[c(1, 3), 1]) # 自営の平均
sum(sum0903$coefficients[c(1, 4), 1]) # 無職の平均

重回帰分析の結果における,各ダミー変数の偏回帰係数のt検定の部分が,有意水準無調整の多重比較(つまり通常の2群でのt検定)に一致する事も以下の様に確認しよう。

有意確率の小数の表示形式が異なるので分かりにくいかも知れないが,この多重比較の表のうち1列目(つまりカテゴリ1と他のカテゴリの比較の検定の有意確率)の数値は,重回帰分析のCoefficientsの"Pr(>|t|)"の列の結果と一致している。つまり,複数のダミー変数の偏回帰係数のt検定は,単純に二群ごとの平均値の比較のt検定を行っている事と同じなのである。異なる点は,通常の多重比較は全てのカテゴリ間の平均値差を検定するのに対して,ダミー変数重回帰では参照カテゴリと他のカテゴリとの平均値差の検定しか行わない点である。例えば上の重回帰例では,非正規と自営の平均値差の有意確率は計算されない。ここからも,どのカテゴリを参照カテゴリとすべきかが重要である事が分かる。
参照カテゴリとの多重比較
ダミー変数重回帰の偏回帰係数のt検定に対応する,有意水準を調整した多重比較の方法に,Dunnett法がある。本文では脚注で簡単に触れただけであるが,ここで実際に実行してみよう。まずは,multcompパッケイジを新たにインストールするところから始める(出力結果は省略)。
# まずは使用する追加パッケイジをインストール(PCにつき1回)
install.packages("multcomp", repos="https://cran.ism.ac.jp")
# インストールしたパッケイジを有効化(Rを新たに起動した場合には必要)
library(multcomp)
group <- factor(data01$job)
resultD <- glht(aov(data01$fincome ~ group), linfct=mcp(group="Dunnett"))
resultD
summary(resultD)
install.packages("multcomp", repos="https://cran.ism.ac.jp")
# インストールしたパッケイジを有効化(Rを新たに起動した場合には必要)
library(multcomp)
group <- factor(data01$job)
resultD <- glht(aov(data01$fincome ~ group), linfct=mcp(group="Dunnett"))
resultD
summary(resultD)

先頭のカテゴリとそれ以外のカテゴリの比較だけが検定されている事が読み取れる。有意確率は,偏回帰係数のt検定や無調整のカテゴリ間t検定の有意確率よりも3倍近く高くなっている事が分かる。これが,検定の多重性を調整した結果である。
confint( )関数を使って,平均値差の信頼区間の出力も可能である。95%信頼区間が,有意水準5%の仮説検定の結果と対応する事はもう理解出来ただろうか。

最後に,独立変数にカテゴリカル変数を指定した線型モデルlm( )の結果がダミー変数重回帰の結果と完全に一致する事を示しておこう。この様にして,同じ事を様々な方法で実行してみる事を通して,それぞれの分析手法についての理解を深めていけると良い。

第9章の【練習問題】の解答
1) の答え: 出力結果は多少省略した。(これまで同様,本文ではデータフレイム名をdataとしているが,サポートウェブではdata01としているので注意されたい。)
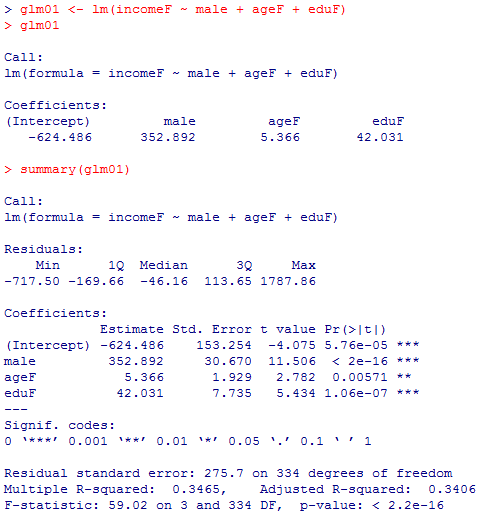
モデルのF検定は1%水準で有意で分散説明率は35%弱,全ての独立変数の偏回帰係数も1%有意である。標本偏回帰係数を見ると,女性より男性は350万円余り個人年収が多く,年齢が1歳上だと5.4万円,教育年数が1年長いと42万円個人年収が多い。
独立変数の設定値をヴェクトル化して,予測値を次の様に計算させる事が出来る。

2) の答え:
モデルの検定結果は1)と全く同じである(そうあるべきである)。標準化偏回帰係数のt検定の結果も,t統計量と有意確率は全く変化しない。係数の値は変化しており,性別>教育年数>年齢の順に絶対値が大きい。よって従属変数に対する効果の大きさはこの順に大きいと言える。
3) の答え:

よく見ると,標準化した年齢と教育年数の結果は2)と全く同じである。男性ダミーは標準化していないので,女性よりも男性の方が個人年収が1標準偏差余り高いと云う事が読み取れる。この影響力は,年齢の8.2標準偏差分,教育年数の4.2標準偏差分に相当する。
2)と3)のどちらがより適切かを言うのは難しいが,そもそも0か1の値しかとらない筈のダミー変数を標準化して「男性ダミー変数が1標準偏差大きいと個人年収が0.51標準偏差大きい」と述べても意味するところが明確だとは思えない。異論もあるかも知れないが,ここではダミー変数に関しては標準化しない立場を提案しておこう。
4) の答え:

glm01におけるeduの偏回帰係数のt検定の結果を参照する。
5) の答え: 男性ダミー変数や従業上の地位というカテゴリカル変数を含む事を考慮し,非標準化解を優先する。参考の為にそれ以外の変数を標準化した解も後で求めておく。

1)の結果と比較すると,分散説明率は35%弱から44%弱に大きく上昇した。男性ダミーの効果は140万円ほど低下している。年齢の効果は微増(10歳で54万円から64万円へ),教育年数の効果は微減(4年で170万円から140万円へ)したが大きな違いではない。新たに追加投入した従業上の地位は正規雇用が参照カテゴリ(基準カテゴリ)になっており,自営は正規より66万円ほど低いが統計的に有意ではない。非正規は正規より220万円有意に低く,無職は正規より300万円有意に低い。男性ダミーの効果の減少分の多くは,従業上の地位の効果に表れたと考えられる。つまり,男女で従業上の地位(特に正規,非正規,無職)の分布が異なり,その影響が最初のモデルでは男性ダミーの係数に反映されていたのだと考えられる。
以下は,ダミー変数以外を標準化した標準化解の結果である。
# 完備ケース分析.変数名を変えて,変換前後の情報を全て残しておく.
# 新変数は,データフレイムdata01の中には含まれていない事に注意.
Full <- complete.cases(data01$income, data01$sex, data01$age, data01$edu)
incomeF <- data01$income[Full]
sexF <- data01$sex[Full]
ageF <- data01$age[Full]
eduF <- data01$edu[Full]
# 男性ダミー変数を作成する
male <- c(1, 0)[sexF]
glm01 <- lm(incomeF ~ male + ageF + eduF)
glm01
summary(glm01)
# 新変数は,データフレイムdata01の中には含まれていない事に注意.
Full <- complete.cases(data01$income, data01$sex, data01$age, data01$edu)
incomeF <- data01$income[Full]
sexF <- data01$sex[Full]
ageF <- data01$age[Full]
eduF <- data01$edu[Full]
# 男性ダミー変数を作成する
male <- c(1, 0)[sexF]
glm01 <- lm(incomeF ~ male + ageF + eduF)
glm01
summary(glm01)

モデルのF検定は1%水準で有意で分散説明率は35%弱,全ての独立変数の偏回帰係数も1%有意である。標本偏回帰係数を見ると,女性より男性は350万円余り個人年収が多く,年齢が1歳上だと5.4万円,教育年数が1年長いと42万円個人年収が多い。
独立変数の設定値をヴェクトル化して,予測値を次の様に計算させる事が出来る。
par_reg <- summary(glm01)$coefficients[, 1]
par_reg
indep <- c(1, 1, 40, 16) # 男性,40歳,四大卒
sum(par_reg*indep) # 個人年収予測値
# 女性,35歳,四大卒の個人年収予測値
sum(par_reg*c(1, 0, 35, 16))
# 女性,50歳,高校卒の個人年収予測値
sum(par_reg*c(1, 0, 50, 12))
par_reg
indep <- c(1, 1, 40, 16) # 男性,40歳,四大卒
sum(par_reg*indep) # 個人年収予測値
# 女性,35歳,四大卒の個人年収予測値
sum(par_reg*c(1, 0, 35, 16))
# 女性,50歳,高校卒の個人年収予測値
sum(par_reg*c(1, 0, 50, 12))

2) の答え:
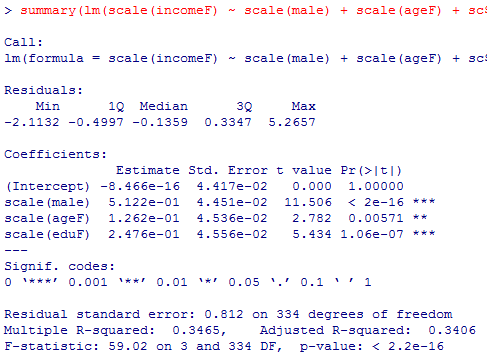
summary(lm(scale(incomeF) ~ scale(male) + scale(ageF) + scale(eduF)))

モデルの検定結果は1)と全く同じである(そうあるべきである)。標準化偏回帰係数のt検定の結果も,t統計量と有意確率は全く変化しない。係数の値は変化しており,性別>教育年数>年齢の順に絶対値が大きい。よって従属変数に対する効果の大きさはこの順に大きいと言える。
3) の答え:
summary(lm(scale(incomeF) ~ male + scale(ageF) + scale(eduF)))

よく見ると,標準化した年齢と教育年数の結果は2)と全く同じである。男性ダミーは標準化していないので,女性よりも男性の方が個人年収が1標準偏差余り高いと云う事が読み取れる。この影響力は,年齢の8.2標準偏差分,教育年数の4.2標準偏差分に相当する。
2)と3)のどちらがより適切かを言うのは難しいが,そもそも0か1の値しかとらない筈のダミー変数を標準化して「男性ダミー変数が1標準偏差大きいと個人年収が0.51標準偏差大きい」と述べても意味するところが明確だとは思えない。異論もあるかも知れないが,ここではダミー変数に関しては標準化しない立場を提案しておこう。
4) の答え:
glm01b <- lm(incomeF ~ male + ageF)
summary(glm01b)
anova(glm01b, glm01)
summary(glm01b)
anova(glm01b, glm01)

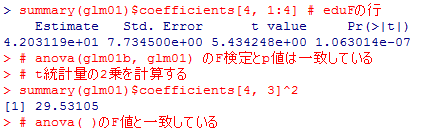
glm01におけるeduの偏回帰係数のt検定の結果を参照する。
summary(glm01)$coefficients[4, 1:4] # eduFの行
# anova(glm01b, glm01) のF検定とp値は一致している
# t統計量の2乗を計算する
summary(glm01)$coefficients[4, 3]^2
# anova( )のF値と一致している
# anova(glm01b, glm01) のF検定とp値は一致している
# t統計量の2乗を計算する
summary(glm01)$coefficients[4, 3]^2
# anova( )のF値と一致している

5) の答え: 男性ダミー変数や従業上の地位というカテゴリカル変数を含む事を考慮し,非標準化解を優先する。参考の為にそれ以外の変数を標準化した解も後で求めておく。
Full <- complete.cases(data01$income, data01$sex, data01$age, data01$edu, data01$job)
incomeF <- data01$income[Full]
maleF <- c(1, 0)[data01$sex[Full]]
ageF <- data01$age[Full]
eduF <- data01$edu[Full]
jobF <- factor(data01$job[Full])
glm01c <- lm(incomeF ~ maleF + ageF + eduF + jobF)
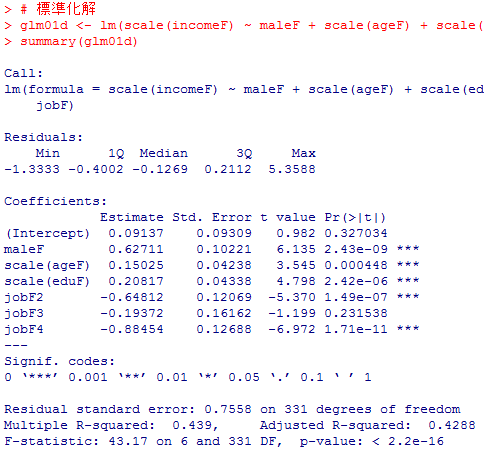
summary(glm01c)
# 標準化解
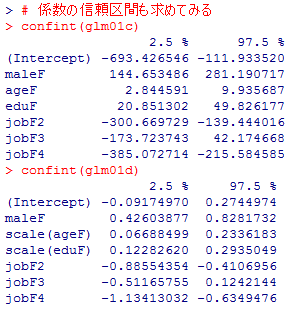
glm01d <- lm(scale(incomeF) ~ maleF + scale(ageF) + scale(eduF) + jobF)
summary(glm01d)
incomeF <- data01$income[Full]
maleF <- c(1, 0)[data01$sex[Full]]
ageF <- data01$age[Full]
eduF <- data01$edu[Full]
jobF <- factor(data01$job[Full])
glm01c <- lm(incomeF ~ maleF + ageF + eduF + jobF)
summary(glm01c)
# 標準化解
glm01d <- lm(scale(incomeF) ~ maleF + scale(ageF) + scale(eduF) + jobF)
summary(glm01d)

1)の結果と比較すると,分散説明率は35%弱から44%弱に大きく上昇した。男性ダミーの効果は140万円ほど低下している。年齢の効果は微増(10歳で54万円から64万円へ),教育年数の効果は微減(4年で170万円から140万円へ)したが大きな違いではない。新たに追加投入した従業上の地位は正規雇用が参照カテゴリ(基準カテゴリ)になっており,自営は正規より66万円ほど低いが統計的に有意ではない。非正規は正規より220万円有意に低く,無職は正規より300万円有意に低い。男性ダミーの効果の減少分の多くは,従業上の地位の効果に表れたと考えられる。つまり,男女で従業上の地位(特に正規,非正規,無職)の分布が異なり,その影響が最初のモデルでは男性ダミーの係数に反映されていたのだと考えられる。
以下は,ダミー変数以外を標準化した標準化解の結果である。


Copyright (C) 2016-2017 SUGINO Isamu All Rights Reserved. design by tempnate

