杉野 勇 (SUGINO Isamu) お茶の水女子大学・人間発達科学専攻・応用社会学コース担当
『入門・社会統計学』サポートウェブ |
|
 第7章 平均値の差の分散分析(ANOVA)
第7章 平均値の差の分散分析(ANOVA)
グループ間の母平均の差を検定する分散分析,ANOVAの初歩について解説する。1-1 偏差平方和(Sum of Squares)の分解
1-2 ゼロ仮説(Null Hypothesis; H0)とF統計量
ここでも本文では紙幅の関係で式変形の途中などを省略したので,もう少し詳しく説明するPDFを上げておく。

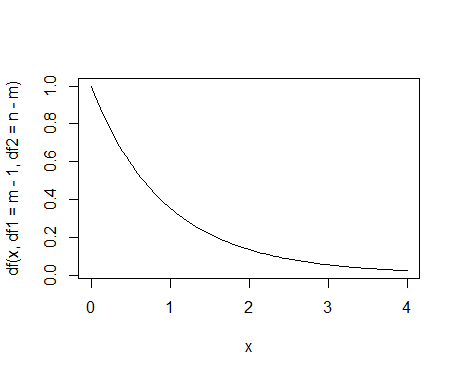
Rでは,自由度df1,df2のF分布の右端5%領域の限界値は,qf(p=.95, df1, df2)もしくはqf(p=.05, df1, df2, lower.tail=F)として求められる。グラフは,curve(df(df1, df2), from=0, to=4) などとすると描ける。以下は,グループの数mが3,総ケース数nが30を想定した数値例である。

グラフにいくつかオプションなどで装飾を施してみよう。

Rでは,自由度df1,df2のF分布の右端5%領域の限界値は,qf(p=.95, df1, df2)もしくはqf(p=.05, df1, df2, lower.tail=F)として求められる。グラフは,curve(df(df1, df2), from=0, to=4) などとすると描ける。以下は,グループの数mが3,総ケース数nが30を想定した数値例である。
m <- 3; n <- 30
qf(p=.95, df1=m-1, df2=n-m)
qf(p=.05, df1=m-1, df2=n-m, lower.tail=F)
curve(df(x, df1=m-1, df2=n-m), from=0, to=4)
qf(p=.95, df1=m-1, df2=n-m)
qf(p=.05, df1=m-1, df2=n-m, lower.tail=F)
curve(df(x, df1=m-1, df2=n-m), from=0, to=4)


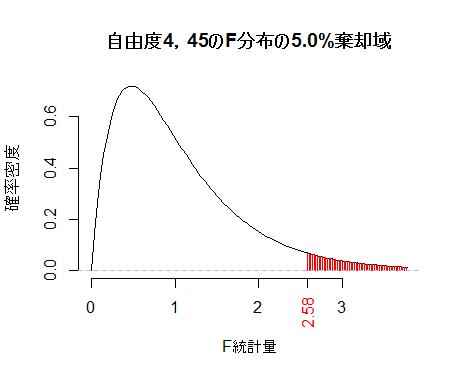
グラフにいくつかオプションなどで装飾を施してみよう。
m <- 5; n <- 50; p0 <- .05
F0 <- qf(p=p0, df1=m-1, df2=n-m, lower.tail=F)
END <- qf(min(p0/2, .01), df1=m-1, df2=n-m, lower.tail=F)
curve(df(x, df1=m-1, df2=n-m), from=0, to=END, bty="n",
xlab="F統計量", ylab="確率密度",
main=sprintf("自由度%d,%dのF分布の%.1f%%棄却域", m-1, n-m, p0*100))
axis(side=1, at=F0, label=round(F0, 2), col.axis="red", las=2)
segments(rej <- seq(F0, END, by=.02), 0,
rej, df(rej, df1=m-1, df2=n-m), col="red")
abline(h=0, lty=2, col="grey")
F0 <- qf(p=p0, df1=m-1, df2=n-m, lower.tail=F)
END <- qf(min(p0/2, .01), df1=m-1, df2=n-m, lower.tail=F)
curve(df(x, df1=m-1, df2=n-m), from=0, to=END, bty="n",
xlab="F統計量", ylab="確率密度",
main=sprintf("自由度%d,%dのF分布の%.1f%%棄却域", m-1, n-m, p0*100))
axis(side=1, at=F0, label=round(F0, 2), col.axis="red", las=2)
segments(rej <- seq(F0, END, by=.02), 0,
rej, df(rej, df1=m-1, df2=n-m), col="red")
abline(h=0, lty=2, col="grey")

1-3 4群の母平均差のF検定
まずは使用する変数の基本的な情報(度数分布や要約統計量,ケース数)を確認しておく必要がある。欠損値NAが含まれる場合はひと手間余計にかかる事が多いので注意しよう。また,本文と異なり,データフレイムの名前はdata01としている。


本文の箱ひげ図は次のスクリプトで描いている。結果は本文にある通りである。
いよいよ(一要因)分散分析を行う。aov( )関数,lm( )関数,oneway.test( )関数のうち,まずは最初の二つを説明する。
■aov( )関数

出力結果を用いて,「グループ平均はすべて等しい」というゼロ仮説の有意性検定をF分布を用いて行う事が出来る。この例ではF統計量は約3.05,有意確率は約2.9%となり,5%水準で有意となった。
■lm( )関数
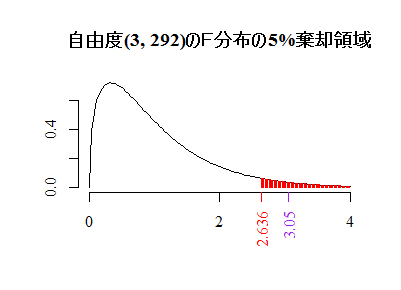
次のスクリプトを実行すると,このF分布の5%棄却域(赤)とF値(紫)の関係をカラーで図示できる。関数ごとに分けて実行すると関数の意味が分かりやすい。
なお,各種の分散説明率(R-squared, Eta-squared, partial Eta-squared)については,二元配置分散分析の2-1 平方和の分解の末尾に例示を付け加えておく。
data01 <- read.csv("practice.csv")
# まずは各変数の度数分布または基本要約統計量を確認
table(data01$job, useNA="always")
summary(data01$fincome)
# 次に,従業上の地位別の世帯年収の要約統計
tapply(data01$fincome, data01$job, summary)
# 各群のケース数は以下のコマンドで分かる様に思えるが,欠損値を含む
tapply(data01$fincome, data01$job, length)
# 欠損値抜きのケース数を求める( Rコマンダー の出力を参考にした)
tapply(data01$fincome, data01$job, function(x) sum(!is.na(x)))
# tableで各群のケース数を求める事も不可能ではない。
t01 <- addmargins(table(data01$job, data01$fincome, useNA="ifany"))
t01
t01[, ncol(t01)] - t01[, ncol(t01)-1]
# まずは各変数の度数分布または基本要約統計量を確認
table(data01$job, useNA="always")
summary(data01$fincome)
# 次に,従業上の地位別の世帯年収の要約統計
tapply(data01$fincome, data01$job, summary)
# 各群のケース数は以下のコマンドで分かる様に思えるが,欠損値を含む
tapply(data01$fincome, data01$job, length)
# 欠損値抜きのケース数を求める( Rコマンダー の出力を参考にした)
tapply(data01$fincome, data01$job, function(x) sum(!is.na(x)))
# tableで各群のケース数を求める事も不可能ではない。
t01 <- addmargins(table(data01$job, data01$fincome, useNA="ifany"))
t01
t01[, ncol(t01)] - t01[, ncol(t01)-1]


本文の箱ひげ図は次のスクリプトで描いている。結果は本文にある通りである。
boxplot(data01$fincome ~ data01$job, varwidth=T,
pars=par(bty="n", family="serif"), las=1,
main="従業上の地位別の世帯年収(万円)",
names=c("正規", "非正規", "自営", "無職"))
pars=par(bty="n", family="serif"), las=1,
main="従業上の地位別の世帯年収(万円)",
names=c("正規", "非正規", "自営", "無職"))
いよいよ(一要因)分散分析を行う。aov( )関数,lm( )関数,oneway.test( )関数のうち,まずは最初の二つを説明する。
■aov( )関数
#### aov
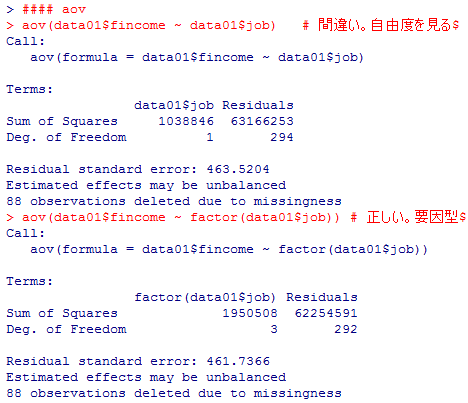
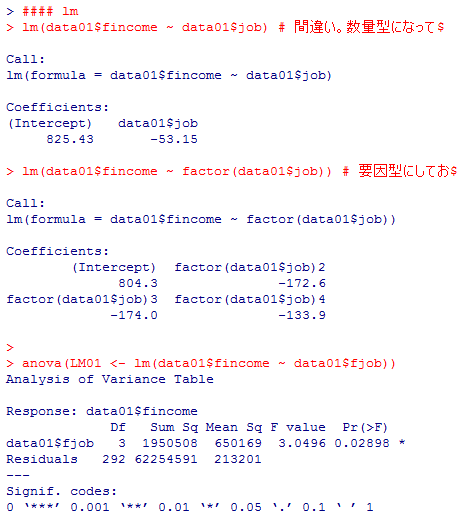
aov(data01$fincome ~ data01$job) # 間違い。自由度を見ると分かる。
aov(data01$fincome ~ factor(data01$job)) # 正しい。要因型にする必要。
# 出力が見にくい場合は,次のようにfactor型の変数を新規作成するのも良い。
data01$fjob <- factor(data01$job, levels=c(1, 2, 3, 4),
labels=c("1 正規", "2 非正規", "3 自営", "4 無職"))
summary(data01$fjob) # 新変数の確認
# aov( )の結果をオブジェクトに格納しておくと便利。名前(ANOVA01)は自由。
ANOVA01 <- aov(data01$fincome ~ data01$fjob)
summary(ANOVA01)
anova(ANOVA01)
aov(data01$fincome ~ data01$job) # 間違い。自由度を見ると分かる。
aov(data01$fincome ~ factor(data01$job)) # 正しい。要因型にする必要。
# 出力が見にくい場合は,次のようにfactor型の変数を新規作成するのも良い。
data01$fjob <- factor(data01$job, levels=c(1, 2, 3, 4),
labels=c("1 正規", "2 非正規", "3 自営", "4 無職"))
summary(data01$fjob) # 新変数の確認
# aov( )の結果をオブジェクトに格納しておくと便利。名前(ANOVA01)は自由。
ANOVA01 <- aov(data01$fincome ~ data01$fjob)
summary(ANOVA01)
anova(ANOVA01)


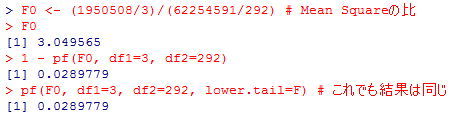
出力結果を用いて,「グループ平均はすべて等しい」というゼロ仮説の有意性検定をF分布を用いて行う事が出来る。この例ではF統計量は約3.05,有意確率は約2.9%となり,5%水準で有意となった。
F0 <- (1950508/3)/(62254591/292) # Mean Squareの比
F0
1 - pf(F0, df1=3, df2=292)
pf(F0, df1=3, df2=292, lower.tail=F) # これでも結果は同じ
F0
1 - pf(F0, df1=3, df2=292)
pf(F0, df1=3, df2=292, lower.tail=F) # これでも結果は同じ

■lm( )関数
#### lm
lm(data01$fincome ~ data01$job) # 間違い。数量型になっている。
lm(data01$fincome ~ factor(data01$job)) # 要因型にしており正しい。
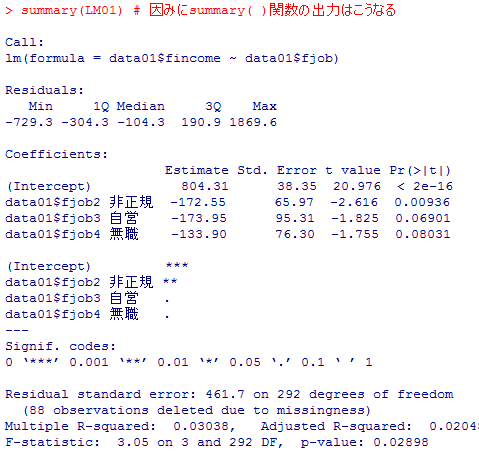
anova(LM01 <- lm(data01$fincome ~ data01$fjob))
summary(LM01) # 因みにsummary( )関数の出力はこうなる
lm(data01$fincome ~ data01$job) # 間違い。数量型になっている。
lm(data01$fincome ~ factor(data01$job)) # 要因型にしており正しい。
anova(LM01 <- lm(data01$fincome ~ data01$fjob))
summary(LM01) # 因みにsummary( )関数の出力はこうなる


次のスクリプトを実行すると,このF分布の5%棄却域(赤)とF値(紫)の関係をカラーで図示できる。関数ごとに分けて実行すると関数の意味が分かりやすい。
# F分布
F0 <- (1950508/3)/(62254591/292) # F統計量
DF1 <- 3; DF2 <- 292 # 自由度は関数のオプションの名称と区別する為敢えて大文字にした
curve(df(x, DF1, DF2), xlim=c(0, END <- 4), xaxp=c(0, END, 2),
bty="n", family="serif", xlab="", ylab="",
main=sprintf("自由度(%d, %d)のF分布の5%%棄却領域", DF1, DF2))
segments(x1 <- seq(x2 <- qf(.95, DF1, DF2), END, by=.02), 0,
x1, df(x1, DF1, DF2), col="red")
axis(side=1, at=round(x2, 3), col="red", col.axis="red", las=2, family="serif")
axis(side=1, at=round(F0, 3), col="purple", col.axis="purple", las=2, family="serif")
F0 <- (1950508/3)/(62254591/292) # F統計量
DF1 <- 3; DF2 <- 292 # 自由度は関数のオプションの名称と区別する為敢えて大文字にした
curve(df(x, DF1, DF2), xlim=c(0, END <- 4), xaxp=c(0, END, 2),
bty="n", family="serif", xlab="", ylab="",
main=sprintf("自由度(%d, %d)のF分布の5%%棄却領域", DF1, DF2))
segments(x1 <- seq(x2 <- qf(.95, DF1, DF2), END, by=.02), 0,
x1, df(x1, DF1, DF2), col="red")
axis(side=1, at=round(x2, 3), col="red", col.axis="red", las=2, family="serif")
axis(side=1, at=round(F0, 3), col="purple", col.axis="purple", las=2, family="serif")

なお,各種の分散説明率(R-squared, Eta-squared, partial Eta-squared)については,二元配置分散分析の2-1 平方和の分解の末尾に例示を付け加えておく。
1-4 多重比較(multiple comparison),事後検定(post-hoc test)
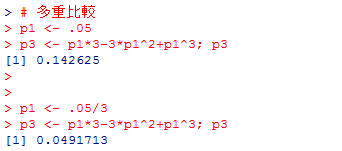
一つ一つの検定の有意水準をp1,そうした検定を3つ繰り返した場合の最終的な有意水準をp3とすると,p3 = p1 + p1 + p1 - 3*p1*p1 + p1*p1*p1 である。p1を.05(5%)とすると,p3=.142625となる。そこでp1=.05/3とすると,p3は5%以内に収まる。
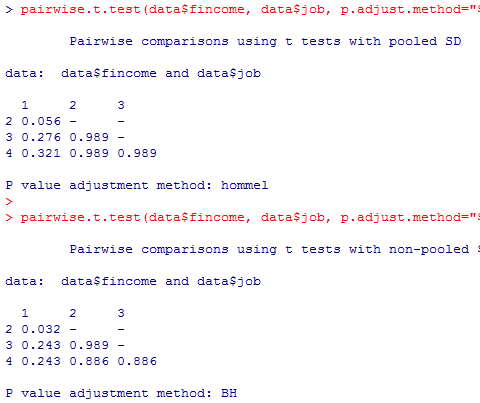
世帯年収fincomeと従業上の地位jobで実際にボンフェローニ法を実行してみよう。共通の標準偏差を用いるか否かというオプションpool.sdによって結果が変わる。本文ではデフォルトのpool.sd=Tの結果を述べたが,ここでは両方実行する。

デフォルトはプールした標準偏差を使う,つまり全ての群で等分散を仮定しているが,pool.sd=Fとすると各群での標準偏差を使用する(等分散を仮定しない)。等分散を仮定しないt検定とはつまりWelchの検定であり,上の出力の後半は,各ペアでウェルチの検定を行って計算された有意確率に検定の回数(ここでは6回)をかけた結果が出力されている。例えばjob=1とjob=2だけでWelchの検定を行うと有意確率は.005345494となる。これに全ての検定のペアの数6をかけると,.03207297となり,上記のボンフェローニ法の結果の1と2の有意確率0.032に一致する。

本文で触れた,無調整の検定結果を一応示しておく。

指定しうる多重比較の方法は,ボンフェローニ"bonferroni",ホルム"holm", ホッホベルク"hochberg", ホンメル"hommel", ベンジャミニとホッホベルク"BH", ベンジャミニとイェクティエリ"BY"である。bonferroni,holm,hochberg,hommelは"family-wise error rate(FWER)"を調整するものであるが,BHとBYは"false discovery rate(FDR)"を統制するものである。以下のサイトの解説が分かり易い。
 『大阪大学大学院医学系研究科 老年・腎臓内科学 腎臓内科』の多重比較解説(2016年10月24日閲覧)
『大阪大学大学院医学系研究科 老年・腎臓内科学 腎臓内科』の多重比較解説(2016年10月24日閲覧)
hommel・等分散の例と,BH・不等分散の実行例を示しておく。
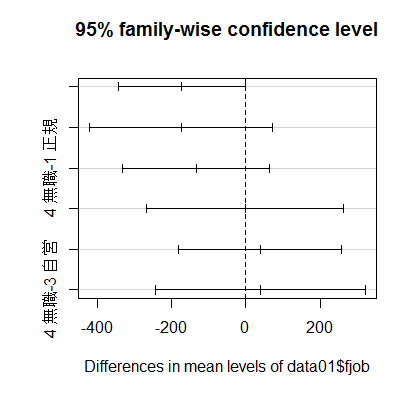
Tukey法は,以下の最初の二行で実行し信頼区間を図示できるが,より見易くする為にオブジェクトの代入を活用したのがその後のスクリプトである。


世帯年収fincomeと従業上の地位jobで実際にボンフェローニ法を実行してみよう。共通の標準偏差を用いるか否かというオプションpool.sdによって結果が変わる。本文ではデフォルトのpool.sd=Tの結果を述べたが,ここでは両方実行する。
# 共通の標準偏差を推定して検定(等分散性の仮定)
pairwise.t.test(data01$fincome, data01$job, p.adjust.method="bonferroni")
# 等分散を仮定しないで検定
pairwise.t.test(data01$fincome, data01$job, p.adjust.method="bonferroni", pool.sd=F)
pairwise.t.test(data01$fincome, data01$job, p.adjust.method="bonferroni")
# 等分散を仮定しないで検定
pairwise.t.test(data01$fincome, data01$job, p.adjust.method="bonferroni", pool.sd=F)

デフォルトはプールした標準偏差を使う,つまり全ての群で等分散を仮定しているが,pool.sd=Fとすると各群での標準偏差を使用する(等分散を仮定しない)。等分散を仮定しないt検定とはつまりWelchの検定であり,上の出力の後半は,各ペアでウェルチの検定を行って計算された有意確率に検定の回数(ここでは6回)をかけた結果が出力されている。例えばjob=1とjob=2だけでWelchの検定を行うと有意確率は.005345494となる。これに全ての検定のペアの数6をかけると,.03207297となり,上記のボンフェローニ法の結果の1と2の有意確率0.032に一致する。
# job=1とjob=2だけでウェルチ検定
welch01 <- t.test(data01$fincome[data01$job==1 | data01$job==2] ~
data01$job[data01$job==1 | data01$job==2], var.equal=F)
welch01
names(welch01)
welch01$"p.value"*6
welch01 <- t.test(data01$fincome[data01$job==1 | data01$job==2] ~
data01$job[data01$job==1 | data01$job==2], var.equal=F)
welch01
names(welch01)
welch01$"p.value"*6

本文で触れた,無調整の検定結果を一応示しておく。

指定しうる多重比較の方法は,ボンフェローニ"bonferroni",ホルム"holm", ホッホベルク"hochberg", ホンメル"hommel", ベンジャミニとホッホベルク"BH", ベンジャミニとイェクティエリ"BY"である。bonferroni,holm,hochberg,hommelは"family-wise error rate(FWER)"を調整するものであるが,BHとBYは"false discovery rate(FDR)"を統制するものである。以下のサイトの解説が分かり易い。
 『大阪大学大学院医学系研究科 老年・腎臓内科学 腎臓内科』の多重比較解説(2016年10月24日閲覧)
『大阪大学大学院医学系研究科 老年・腎臓内科学 腎臓内科』の多重比較解説(2016年10月24日閲覧)hommel・等分散の例と,BH・不等分散の実行例を示しておく。

Tukey法は,以下の最初の二行で実行し信頼区間を図示できるが,より見易くする為にオブジェクトの代入を活用したのがその後のスクリプトである。
# Tukey法の実行と信頼区間の作図
TukeyHSD(aov(data01$fincome ~ factor(data01$job)))
plot(TukeyHSD(aov(data01$fincome ~ factor(data01$job))))
# 同じことを,もう少し見易く書いたのが以下
data01$fjob <- factor(data01$job, levels=c(1, 2, 3, 4),
labels=c("1 正規", "2 非正規", "3 自営", "4 無職"))
ANOVA01 <- aov(data01$fincome ~ data01$fjob)
TukeyHSD(ANOVA01)
plot(TukeyHSD(ANOVA01))
TukeyHSD(aov(data01$fincome ~ factor(data01$job)))
plot(TukeyHSD(aov(data01$fincome ~ factor(data01$job))))
# 同じことを,もう少し見易く書いたのが以下
data01$fjob <- factor(data01$job, levels=c(1, 2, 3, 4),
labels=c("1 正規", "2 非正規", "3 自営", "4 無職"))
ANOVA01 <- aov(data01$fincome ~ data01$fjob)
TukeyHSD(ANOVA01)
plot(TukeyHSD(ANOVA01))


1-5 等分散性の前提とウェルチ検定
次のスクリプトの一行目がデフォルトの(等分散性を仮定しない)一要因分散分析,二行目が等分散の仮定を指定した一要因分散分析である。後者の結果は,先に紹介したaov( )やlm( )と一致している事を見比べよう。


# 一元配置分散分析
oneway.test(data01$fincome ~ data01$job)
oneway.test(data01$fincome ~ data01$job, var.equal=T)
oneway.test(data01$fincome ~ data01$job)
oneway.test(data01$fincome ~ data01$job, var.equal=T)

等分散性の検定
本文では簡単に触れているだけの等分散性の検定を実際に行ってみる。標準で存在しているバートレット検定bartlett.test( )と,追加パッケイジ"car"に入っているルヴィーン検定(レヴィン検定)の二つを行ってみよう。"car"パッケイジは,インストールした事がなければ最初にインストールし,その後も使用する際にはlibrary(car)として有効化しなければならない。また,bartlettはグループ変数がfactor型になっていなくても自動で要因型だと見做して分析するが,LeveneTestはfactor型にしなければならない。
# 等分散性検定
bartlett.test(data01$fincome ~ data01$job)
# "car"パッケイジをインストール
install.packages("car", repos="http://cran.ism.ac.jp/")
library(car)
leveneTest(data01$fincome ~ data01$job)
出力結果ではインストールの部分は省略した。bartlett.test(data01$fincome ~ data01$job)
# "car"パッケイジをインストール
install.packages("car", repos="http://cran.ism.ac.jp/")
library(car)
leveneTest(data01$fincome ~ data01$job)

2-1 平方和の分解
二要因分散分析でも,(偏差)平方和SSの分解が基本であることには変わらないが,各グループのサイズが異なる場合(非釣り合い型データ,アンバランスデータ,非直交なデータ)には分解の仕方が複数存在し,標準のaov( )関数はその点で問題を生じる。まずはデータの準備をする。分割表でも分かる様に,セルのサイズ(グループのサイズ)はまるでばらばらである。

次に,それぞれの一要因分散分析と,性別,従業上の地位の順に変数を並べた二要因分散分析の結果を表示する。一要因の場合とは,各独立変数(主効果)の平方和も有意確率も異なる。

ここで,独立変数の並べ順を変えてみよう。変数の並べ順を変えただけで,それぞれの独立変数の偏差平方和も有意確率もすっかり変わってしまった
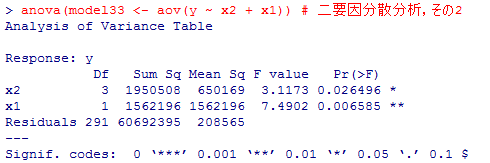
ここで,"car"パッケイジのAnova( )関数を利用する。パッケイジのインストールには上の1-5を参照。model32とmodel33は既に上で作成した分散分析のモデルである。この,投入順を変えた二つのモデルで,Anovaのタイプ?平方和の計算による分散分析を行った結果は,平方和も有意確率も全て一致していて,投入順に左右されない事が確認出来る。因みに,Anova( )関数でタイプ?の平方和を用いる事も出来る(type=3というオプションを付ける)。
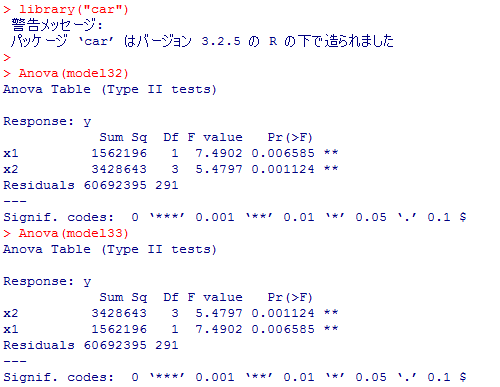
model32,model33自体は以下の通りであり,Anova( )関数を使わなければtype?の計算は行われない。
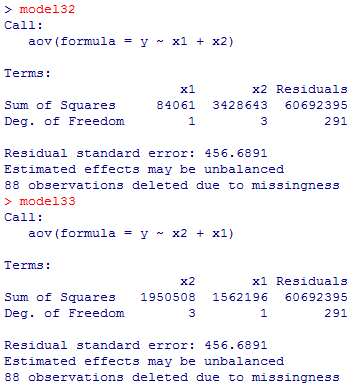
各グループのケース数や年収の平均といった基本的な情報を求めるには以下の様にすれば良い。

分散分析では伝統的にη2(イータの二乗)と云う単語・統計量が使用され,回帰分析ではR2(決定係数)が用いられてきた。R2は通常,モデル全体の説明率を示すのに用いられ,η2は個々の要因の説明率を示すのに用いられる。(重回帰分析では偏回帰係数のt検定は分散説明率の増加分についてのF検定と同値であるので,実際には回帰分析でも個々の要因の説明率を示すのにも使用可能である。)
世帯収入を,性別と従業上の地位で説明するモデルを,aov( )とlm( )で実行し,anova( )やAnova( ),heplotsパッケイジ中のetasq( )関数に与えて出力結果を確認する。

以下に,偏イータの二乗とイータの二乗の計算の仕方を実行例とともに示す。解読してみよう。定義上必ず偏イータの二乗の方が大きくなる。

## 二元配置の分散分析
y <- data01$fincome # 従属変数(被説明変数)
x1 <- factor(data01$sex, levels=1:2,
labels=c("1 男性", "2 女性")) # 独立変数その1
x2 <- factor(data01$job, levels=1:4,
labels=c("1 正規", "2 非正規", "3 自営", "4 無職") ) # 独立変数その2
table("性別"=x1, "従業上の地位"=x2, useNA="ifany")
y <- data01$fincome # 従属変数(被説明変数)
x1 <- factor(data01$sex, levels=1:2,
labels=c("1 男性", "2 女性")) # 独立変数その1
x2 <- factor(data01$job, levels=1:4,
labels=c("1 正規", "2 非正規", "3 自営", "4 無職") ) # 独立変数その2
table("性別"=x1, "従業上の地位"=x2, useNA="ifany")

次に,それぞれの一要因分散分析と,性別,従業上の地位の順に変数を並べた二要因分散分析の結果を表示する。一要因の場合とは,各独立変数(主効果)の平方和も有意確率も異なる。
anova(model30 <- aov(y ~ x1)) # 性別の一要因分散分析
anova(model31 <- aov(y ~ x2)) # 従業上の地位の一要因分散分析
anova(model32 <- aov(y ~ x1 + x2)) # 二要因分散分析,その1
anova(model31 <- aov(y ~ x2)) # 従業上の地位の一要因分散分析
anova(model32 <- aov(y ~ x1 + x2)) # 二要因分散分析,その1

ここで,独立変数の並べ順を変えてみよう。変数の並べ順を変えただけで,それぞれの独立変数の偏差平方和も有意確率もすっかり変わってしまった
anova(model33 <- aov(y ~ x2 + x1)) # 二要因分散分析,その2

ここで,"car"パッケイジのAnova( )関数を利用する。パッケイジのインストールには上の1-5を参照。model32とmodel33は既に上で作成した分散分析のモデルである。この,投入順を変えた二つのモデルで,Anovaのタイプ?平方和の計算による分散分析を行った結果は,平方和も有意確率も全て一致していて,投入順に左右されない事が確認出来る。因みに,Anova( )関数でタイプ?の平方和を用いる事も出来る(type=3というオプションを付ける)。
library("car")
Anova(model32)
Anova(model33)
Anova(model32)
Anova(model33)

model32,model33自体は以下の通りであり,Anova( )関数を使わなければtype?の計算は行われない。

各グループのケース数や年収の平均といった基本的な情報を求めるには以下の様にすれば良い。
tapply(y[!is.na(x2)], x1[!is.na(x2)], mean, na.rm=T) # 性別での平均
tapply(y[!is.na(x1)], x2[!is.na(x1)], mean, na.rm=T) # 従業上の地位での平均
table(x1[!is.na(y)&!is.na(x2)], useNA="ifany") # 有効ケース数
tapply(y[!is.na(x1)], x2[!is.na(x1)], mean, na.rm=T) # 従業上の地位での平均
table(x1[!is.na(y)&!is.na(x2)], useNA="ifany") # 有効ケース数

# 次の様に,有効ケースのみを選び出してから集計・分析する事も出来る。
y0 <- y[complete.cases(y, x1, x2)]
x10 <- x1[complete.cases(y, x1, x2)]
x20 <- x2[complete.cases(y, x1, x2)]
tapply(y0, x10, mean)
tapply(y0, x20, mean)
addmargins(table(x10, x20))
y0 <- y[complete.cases(y, x1, x2)]
x10 <- x1[complete.cases(y, x1, x2)]
x20 <- x2[complete.cases(y, x1, x2)]
tapply(y0, x10, mean)
tapply(y0, x20, mean)
addmargins(table(x10, x20))

分散説明率(Proportion of variance explained)
ここで,効果サイズ(effect size)の指標である分散説明率について紹介しておこう。分散分析では伝統的にη2(イータの二乗)と云う単語・統計量が使用され,回帰分析ではR2(決定係数)が用いられてきた。R2は通常,モデル全体の説明率を示すのに用いられ,η2は個々の要因の説明率を示すのに用いられる。(重回帰分析では偏回帰係数のt検定は分散説明率の増加分についてのF検定と同値であるので,実際には回帰分析でも個々の要因の説明率を示すのにも使用可能である。)
世帯収入を,性別と従業上の地位で説明するモデルを,aov( )とlm( )で実行し,anova( )やAnova( ),heplotsパッケイジ中のetasq( )関数に与えて出力結果を確認する。
## 各種の分散説明率
y <- data01$fincome # 世帯収入が従属変数(被説明変数)
x1 <- factor(data01$sex, levels=1:2,
labels=c("1 男性", "2 女性")) # 独立変数:性別
x2 <- factor(data01$job, levels=1:4,
labels=c("1 正規", "2 非正規", "3 自営", "4 無職") ) # 独立変数:従業上の地位
out01 <- aov(y ~ x1 * x2) # aovの結果
out02 <- lm(y ~ x1 * x2) # lmの結果
anova(out01) # type I SS
sum(anova(out01)$"Sum Sq"[1:3])/sum(anova(out01)$"Sum Sq") # R2を手計算
summary(out02) # lm()の結果からR-squared
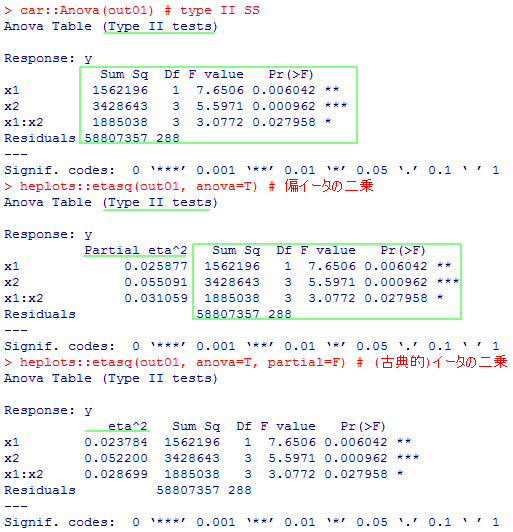
car::Anova(out01) # type II SS
heplots::etasq(out01, anova=T) # 偏イータの二乗
heplots::etasq(out01, anova=T, partial=F) # (古典的)イータの二乗
y <- data01$fincome # 世帯収入が従属変数(被説明変数)
x1 <- factor(data01$sex, levels=1:2,
labels=c("1 男性", "2 女性")) # 独立変数:性別
x2 <- factor(data01$job, levels=1:4,
labels=c("1 正規", "2 非正規", "3 自営", "4 無職") ) # 独立変数:従業上の地位
out01 <- aov(y ~ x1 * x2) # aovの結果
out02 <- lm(y ~ x1 * x2) # lmの結果
anova(out01) # type I SS
sum(anova(out01)$"Sum Sq"[1:3])/sum(anova(out01)$"Sum Sq") # R2を手計算
summary(out02) # lm()の結果からR-squared
car::Anova(out01) # type II SS
heplots::etasq(out01, anova=T) # 偏イータの二乗
heplots::etasq(out01, anova=T, partial=F) # (古典的)イータの二乗


以下に,偏イータの二乗とイータの二乗の計算の仕方を実行例とともに示す。解読してみよう。定義上必ず偏イータの二乗の方が大きくなる。
# 偏イータの二乗の計算方法
eta01 <- heplots::etasq(out01, anova=T); eta01
eta01$"Sum Sq"[c(1:3)]/(eta01$"Sum Sq"[c(1:3)] + eta01$"Sum Sq"[4])
# (古典的)イータの二乗の計算方法
eta02 <- heplots::etasq(out01, anova=T, partial=F); eta02
eta02$"Sum Sq"[c(1:3)]/sum(eta02$"Sum Sq"[1:4])
eta01 <- heplots::etasq(out01, anova=T); eta01
eta01$"Sum Sq"[c(1:3)]/(eta01$"Sum Sq"[c(1:3)] + eta01$"Sum Sq"[4])
# (古典的)イータの二乗の計算方法
eta02 <- heplots::etasq(out01, anova=T, partial=F); eta02
eta02$"Sum Sq"[c(1:3)]/sum(eta02$"Sum Sq"[1:4])

2-2 交互作用項(interaction)
複数の要因(独立変数)が複合的に従属変数に影響を及ぼす事を,計量分析では「交互作用intraction」と呼ぶが,質的比較分析(QCA, Qualitative Comparative Analysis)でいう「結合因果conjunctural causation」と同種の考えであると言ってよいだろう。
以下,本文のスクリプトとその結果を,より装飾を施した形で紹介してゆく。

平方和の分解方法によって結果が異なる事を確認しておこう。
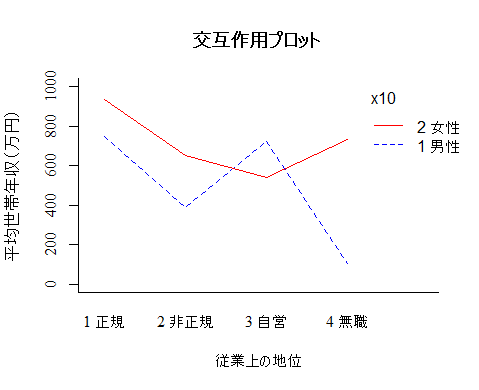
最後に,交互作用プロットの描き方を紹介する。本文のと類似のグラフが以下のスクリプトで描ける。
以下,本文のスクリプトとその結果を,より装飾を施した形で紹介してゆく。
# 性別×従業上の地位によって8つの群に分けた時の世帯年収平均
# 本文では小数点以下が表示されているが,不要なので工夫する。
round(tapply(y, list(x1, x2), mean, na.rm=T), 0)
# 交互作用項を含むモデルの二つの書き方
aov(y ~ x1 + x2 + x1:x2)
aov(y ~ x1 * x2)
# 本文では小数点以下が表示されているが,不要なので工夫する。
round(tapply(y, list(x1, x2), mean, na.rm=T), 0)
# 交互作用項を含むモデルの二つの書き方
aov(y ~ x1 + x2 + x1:x2)
aov(y ~ x1 * x2)

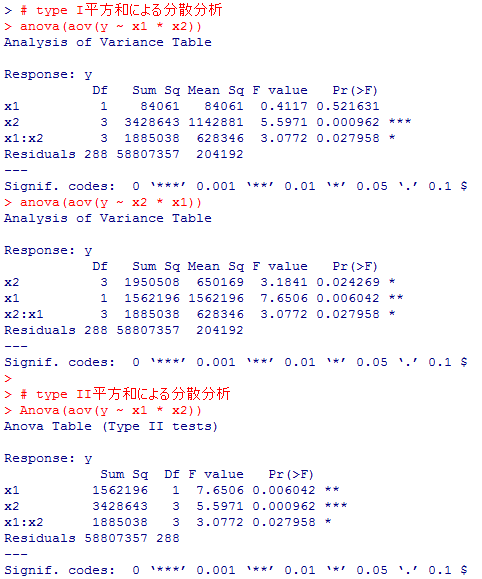
# type I平方和による分散分析
anova(aov(y ~ x1 * x2))
anova(aov(y ~ x2 * x1))
# type II平方和による分散分析
Anova(aov(y ~ x1 * x2))
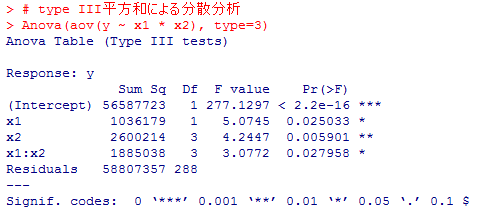
# type III平方和による分散分析
Anova(aov(y ~ x1 * x2), type=3)
anova(aov(y ~ x1 * x2))
anova(aov(y ~ x2 * x1))
# type II平方和による分散分析
Anova(aov(y ~ x1 * x2))
# type III平方和による分散分析
Anova(aov(y ~ x1 * x2), type=3)


平方和の分解方法によって結果が異なる事を確認しておこう。
最後に,交互作用プロットの描き方を紹介する。本文のと類似のグラフが以下のスクリプトで描ける。
interaction.plot(x20, x10, y0, bty="l",
xlab="従業上の地位", ylab="平均世帯年収(万円)", family="serif",
main="交互作用プロット", ylim=c(0,1000), col=c("blue", "red"))
xlab="従業上の地位", ylab="平均世帯年収(万円)", family="serif",
main="交互作用プロット", ylim=c(0,1000), col=c("blue", "red"))

発展1 2群の母平均の差のt検定と1要因分散分析
性別による幸福度の平均の差の分析結果を再掲しておこう。
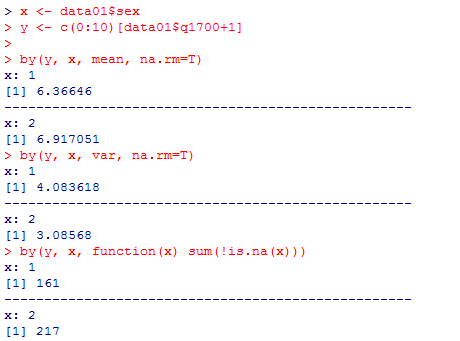
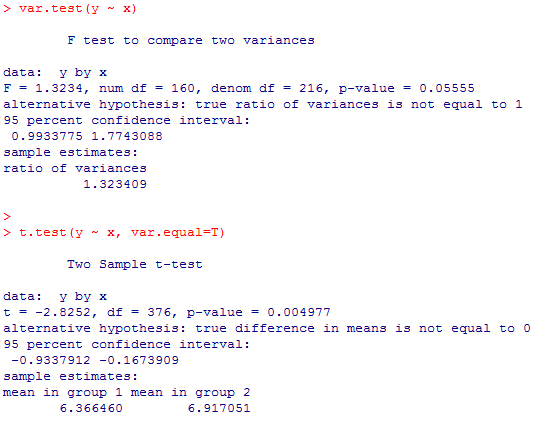
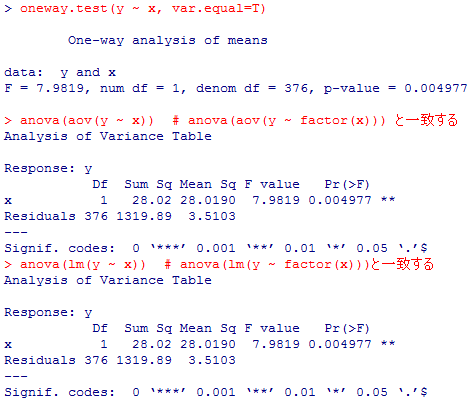
これを,一要因分散分析で行ってみる。この例では等分散を仮定出来る為,関数は3種類あるので全て実行して見せよう。独立変数であるx(元はdata01$sex)はfactor型にすべきだが,二値変数の場合には結果に本質的な違いはない。
t検定の結果とF検定の結果をそれぞれオブジェクトに格納し,並べて表示させよう。更に,オブジェクトにどんな情報が格納されているのかも一覧を確認しよう。

t分布の自由度とF分布の残差(級内)の自由度,有意確率同士が対応している事が分かる。
t統計量とF統計量の関係は,次の様に確認してみよう。
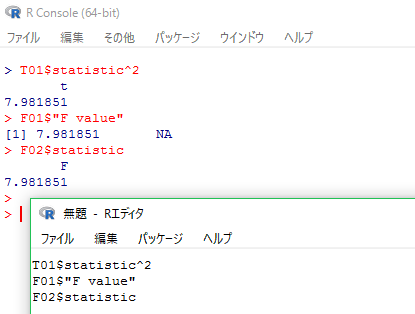
t分布はマイナス領域とプラス領域がある。二乗すれば同じ値になる点が正負の二つある。F分布は全て非負である。どの様に対応しているだろうか。下の様に確認すると,tが負の時と正の時の確率を合わせたものが,(tの二乗に等しい)Fの上側確率に等しい事が分かる。tの両側検定はFの上側検定に対応しているのである。

等分散を仮定出来ずにウェルチの検定を行った,男女での世帯年収差はどうであろうか。

これもやはり,自由度,有意確率が一致し,t統計量の2乗とF統計量が一致している。anova(aov( ))関数では等分散性が仮定出来ない分散分析を行う事は出来ない。
x <- data01$sex
y <- c(0:10)[data01$q1700+1]
by(y, x, mean, na.rm=T)
by(y, x, var, na.rm=T)
by(y, x, function(x) sum(!is.na(x)))
var.test(y ~ x)
t.test(y ~ x, var.equal=T)
y <- c(0:10)[data01$q1700+1]
by(y, x, mean, na.rm=T)
by(y, x, var, na.rm=T)
by(y, x, function(x) sum(!is.na(x)))
var.test(y ~ x)
t.test(y ~ x, var.equal=T)


これを,一要因分散分析で行ってみる。この例では等分散を仮定出来る為,関数は3種類あるので全て実行して見せよう。独立変数であるx(元はdata01$sex)はfactor型にすべきだが,二値変数の場合には結果に本質的な違いはない。
oneway.test(y ~ x, var.equal=T)
anova(aov(y ~ x)) # anova(aov(y ~ factor(x))) と一致する
anova(lm(y ~ x)) # anova(lm(y ~ factor(x)))と一致する
anova(aov(y ~ x)) # anova(aov(y ~ factor(x))) と一致する
anova(lm(y ~ x)) # anova(lm(y ~ factor(x)))と一致する

t検定の結果とF検定の結果をそれぞれオブジェクトに格納し,並べて表示させよう。更に,オブジェクトにどんな情報が格納されているのかも一覧を確認しよう。
T01 <- t.test(y ~ x, var.equal=T)
F01 <- anova(aov(y ~ x))
F02 <- oneway.test(y ~ x, var.equal=T)
T01; names(T01)
F01; names(F01)
F02; names(F02)
F01 <- anova(aov(y ~ x))
F02 <- oneway.test(y ~ x, var.equal=T)
T01; names(T01)
F01; names(F01)
F02; names(F02)

t分布の自由度とF分布の残差(級内)の自由度,有意確率同士が対応している事が分かる。
t統計量とF統計量の関係は,次の様に確認してみよう。

t分布はマイナス領域とプラス領域がある。二乗すれば同じ値になる点が正負の二つある。F分布は全て非負である。どの様に対応しているだろうか。下の様に確認すると,tが負の時と正の時の確率を合わせたものが,(tの二乗に等しい)Fの上側確率に等しい事が分かる。tの両側検定はFの上側検定に対応しているのである。
# t分布の下側確率と上側確率の和
1 - pt(abs(T01$statistic), df=T01$parameter) + pt(-1*abs(T01$statistic), df=T01$parameter)
# F分布の上側確率
1 - pf(F01$"F value"[1], df1=F01$Df[1], df2=F01$Df[2])
1 - pt(abs(T01$statistic), df=T01$parameter) + pt(-1*abs(T01$statistic), df=T01$parameter)
# F分布の上側確率
1 - pf(F01$"F value"[1], df1=F01$Df[1], df2=F01$Df[2])

等分散を仮定出来ずにウェルチの検定を行った,男女での世帯年収差はどうであろうか。
x <- data01$sex
y <- data01$fincome
T01 <- t.test(y ~ x)
F02 <- oneway.test(y ~ x)
T01
F02
T01$statistic^2
F02$statistic
y <- data01$fincome
T01 <- t.test(y ~ x)
F02 <- oneway.test(y ~ x)
T01
F02
T01$statistic^2
F02$statistic

これもやはり,自由度,有意確率が一致し,t統計量の2乗とF統計量が一致している。anova(aov( ))関数では等分散性が仮定出来ない分散分析を行う事は出来ない。
第7章の【練習問題】の解答
1) の答え: 問題文で要求されていないコマンドも含んだスクリプトを,二つに分けて結果と共に掲載する。


2) の答え: まず,anova(aov( ))では独立変数の投入順が結果に影響する事を確認しておく(タイプ?平方和)。
"car"パッケイジのAnova( )関数(タイプ?平方和)ではそうした違いが生じない事を次に確認し,交互作用を含んだモデルも実行する。そして最後に交互作用プロットを描く。
3) の答え: 交互作用含むモデルを取り上げ,aov( ),anova( ),Anova( )の結果も比較してみる。


model1の"coefficients"を表示させると以下の通りである。

カテゴリごとの平均は以下の通りである。

これをよく見比べると,model1$coefficients の(Intercept)は,高校―男性カテゴリの平均個人年収に一致している。また,「x2女性」の-300.9495465は,高校―男性と高校―女性の差にぴったり一致している。「x短大」の61.3189720は高校―男性と短大―男性の差にぴったり一致する。最終学歴においては「高校」が,性別においては「男性」が「基準カテゴリ」となっており,そこからの差が"coefficients"として計算されているのである。これは「ダミー変数を用いて,交互作用項も投入した重回帰分析」と同じである。
ちょっと難しいかも知れないが,この coefficients を次の様に合計すると,各カテゴリの平均が求められる。いずれも最後の列の Sum が,上で調べた各カテゴリの平均年収に一致している事を確認しよう。

以下の様にも計算出来る。この方がダミー変数を投入した重回帰分析の考え方をよく表現している。
x <- factor(data01$edu2, levels=1:3, labels=c("高校", "短大", "四大"))
y <- data01$income
# まずは変数の分布を確認しておく
table(x, useNA="always")
table(y, useNA="always")
# カテゴリー別の平均値,ケース数を求める
by(y, x, mean, na.rm=T)
by(y, x, function(x) sum(!is.na(x)))
y <- data01$income
# まずは変数の分布を確認しておく
table(x, useNA="always")
table(y, useNA="always")
# カテゴリー別の平均値,ケース数を求める
by(y, x, mean, na.rm=T)
by(y, x, function(x) sum(!is.na(x)))

# 等分散性の検定
bartlett.test(y ~ x)
# 等分散を仮定しない分散分析と,仮定する分散分析
oneway.test(y ~ x)
anova(aov(y ~ x))
# 多重比較
TukeyHSD(aov(y ~ x))
bartlett.test(y ~ x)
# 等分散を仮定しない分散分析と,仮定する分散分析
oneway.test(y ~ x)
anova(aov(y ~ x))
# 多重比較
TukeyHSD(aov(y ~ x))

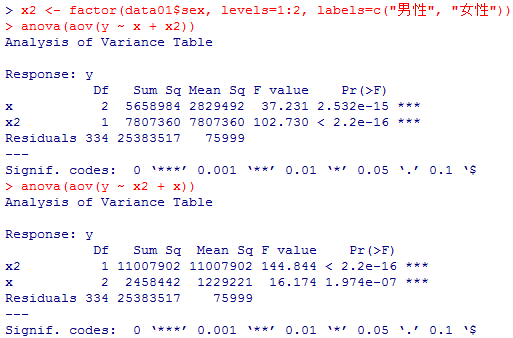
2) の答え: まず,anova(aov( ))では独立変数の投入順が結果に影響する事を確認しておく(タイプ?平方和)。
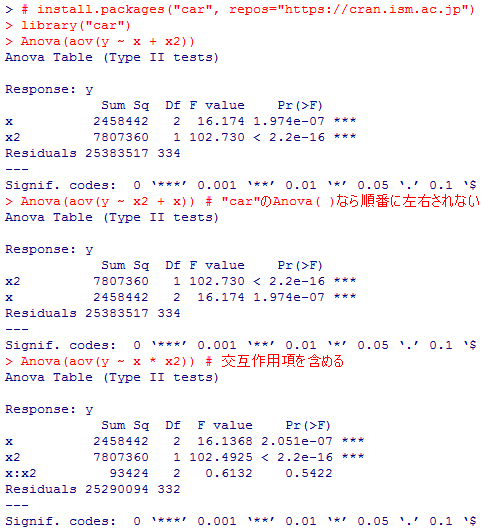
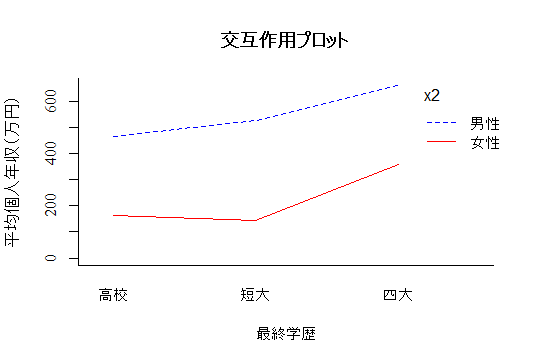
"car"パッケイジのAnova( )関数(タイプ?平方和)ではそうした違いが生じない事を次に確認し,交互作用を含んだモデルも実行する。そして最後に交互作用プロットを描く。
x2 <- factor(data01$sex, levels=1:2, labels=c("男性", "女性"))
# anova(aov( ))では投入順で結果が変わる
anova(aov(y ~ x + x2))
anova(aov(y ~ x2 + x))
# anova(aov( ))では投入順で結果が変わる
anova(aov(y ~ x + x2))
anova(aov(y ~ x2 + x))

# install.packages("car", repos="https://cran.ism.ac.jp")
library("car")
Anova(aov(y ~ x + x2))
Anova(aov(y ~ x2 + x)) # "car"のAnova( )なら順番に左右されない
Anova(aov(y ~ x * x2)) # 交互作用項を含める
library("car")
Anova(aov(y ~ x + x2))
Anova(aov(y ~ x2 + x)) # "car"のAnova( )なら順番に左右されない
Anova(aov(y ~ x * x2)) # 交互作用項を含める

full <- complete.cases(y, x, x2) # 完備ケースだけを選び出す為の準備
y <- y[full]; x <- x[full]; x2 <- x2[full] # 完備ケースの選び出し
MAX <- max(tapply(y, list(x, x2), mean)) # y軸の最大値を自動で設定させる
interaction.plot(x, x2, y, bty="l",
xlab="最終学歴", ylab="平均個人年収(万円)", family="serif",
main="交互作用プロット", ylim=c(0, MAX), col=c("blue", "red"))
y <- y[full]; x <- x[full]; x2 <- x2[full] # 完備ケースの選び出し
MAX <- max(tapply(y, list(x, x2), mean)) # y軸の最大値を自動で設定させる
interaction.plot(x, x2, y, bty="l",
xlab="最終学歴", ylab="平均個人年収(万円)", family="serif",
main="交互作用プロット", ylim=c(0, MAX), col=c("blue", "red"))

3) の答え: 交互作用含むモデルを取り上げ,aov( ),anova( ),Anova( )の結果も比較してみる。
model1 <- aov(y ~ x * x2)
model1 # aov( )のオブジェクトの主な内容
names(model1)
anova(model1) # anova( )の主な内容
names(anova(model1))
Anova(model1) # Anova( )の主な内容
names(Anova(model1))
model1 # aov( )のオブジェクトの主な内容
names(model1)
anova(model1) # anova( )の主な内容
names(anova(model1))
Anova(model1) # Anova( )の主な内容
names(Anova(model1))


model1の"coefficients"を表示させると以下の通りである。

カテゴリごとの平均は以下の通りである。

これをよく見比べると,model1$coefficients の(Intercept)は,高校―男性カテゴリの平均個人年収に一致している。また,「x2女性」の-300.9495465は,高校―男性と高校―女性の差にぴったり一致している。「x短大」の61.3189720は高校―男性と短大―男性の差にぴったり一致する。最終学歴においては「高校」が,性別においては「男性」が「基準カテゴリ」となっており,そこからの差が"coefficients"として計算されているのである。これは「ダミー変数を用いて,交互作用項も投入した重回帰分析」と同じである。
ちょっと難しいかも知れないが,この coefficients を次の様に合計すると,各カテゴリの平均が求められる。いずれも最後の列の Sum が,上で調べた各カテゴリの平均年収に一致している事を確認しよう。
b0 <- model1$coefficients # 係数をオブジェクトに格納する
b <- matrix(c(rep(b0[1], 3), 0, b0[2:3], rep(b0[4], 3), 0, b0[5:6]), ncol=4)
rownames(b) <- c("高校", "短大", "四大")
colnames(b) <- c("基準", "学歴", "女性", "女性×学歴")
b # 係数行列から,基準値(高校―男性),学歴の主効果,性別の主効果,学歴×性別の交互作用効果を構成
addmargins(b[, 1:2])[1:3,] # 男性の各カテゴリはこの様に計算する
addmargins(b)[1:3,] # 女性の各カテゴリはこの様に計算する
b <- matrix(c(rep(b0[1], 3), 0, b0[2:3], rep(b0[4], 3), 0, b0[5:6]), ncol=4)
rownames(b) <- c("高校", "短大", "四大")
colnames(b) <- c("基準", "学歴", "女性", "女性×学歴")
b # 係数行列から,基準値(高校―男性),学歴の主効果,性別の主効果,学歴×性別の交互作用効果を構成
addmargins(b[, 1:2])[1:3,] # 男性の各カテゴリはこの様に計算する
addmargins(b)[1:3,] # 女性の各カテゴリはこの様に計算する

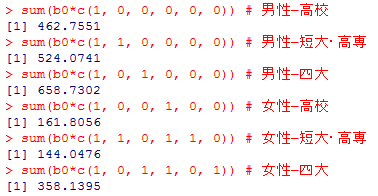
以下の様にも計算出来る。この方がダミー変数を投入した重回帰分析の考え方をよく表現している。
sum(b0*c(1, 0, 0, 0, 0, 0)) # 男性―高校
sum(b0*c(1, 1, 0, 0, 0, 0)) # 男性―短大・高専
sum(b0*c(1, 0, 1, 0, 0, 0)) # 男性―四大
sum(b0*c(1, 0, 0, 1, 0, 0)) # 女性―高校
sum(b0*c(1, 1, 0, 1, 1, 0)) # 女性―短大・高専
sum(b0*c(1, 0, 1, 1, 0, 1)) # 女性―四大
sum(b0*c(1, 1, 0, 0, 0, 0)) # 男性―短大・高専
sum(b0*c(1, 0, 1, 0, 0, 0)) # 男性―四大
sum(b0*c(1, 0, 0, 1, 0, 0)) # 女性―高校
sum(b0*c(1, 1, 0, 1, 1, 0)) # 女性―短大・高専
sum(b0*c(1, 0, 1, 1, 0, 1)) # 女性―四大

Copyright (C) 2016-2017 SUGINO Isamu All Rights Reserved. design by tempnate


