杉野 勇 (SUGINO Isamu) お茶の水女子大学・人間発達科学専攻・応用社会学コース担当
『入門・社会統計学』サポートウェブ |
|
 第1章 1変量の記述統計の基礎
第1章 1変量の記述統計の基礎
一つの数量変数(間隔尺度以上)を特徴付けるのがこの章の核である。以下でも多くのコマンド,スクリプトを例示するので,できるかぎり自分でもRで実際に実習することによって理解を深めよう。1-1 尺度水準(level of scales)と変数(variable)の分類法
平たく言えば「変数(variable)の種類」に相当する尺度水準(level of scales, scale level)は,測定水準(測定のレヴェル,levels of measurement)や測定尺度(measurement scales, scales of measurement)などとも言われ,level, scale, measurementの3つの語がやや入り組んでいて必ずしも厳密に使い分けられているとは言えない。
よく見られる変数の分類法と測定尺度の関係を表に纏めてみる。表の上段ほど尺度水準が低く,言い換えれば含まれる情報量が少なく,表の下段ほど水準が高い,つまり含まれる情報量が多い。
「質的/量的」の二分法を使用しない理由については『入門・社会調査法〔第3版〕』第2章を参照して欲しい。
区別が難しい場合があるのは,「順序尺度/間隔尺度」と「間隔尺度/比例尺度」であるが,後者の「間隔尺度/比例尺度」については,本書のレヴェルでは無理して区別しなくても支障ない。
「間隔尺度/比例尺度」の区別の例としてよく見るのは,温度の単位の「摂氏温度℃」と「華氏温度℉」である。日本で20℃と表現する気温は,アメリカ合衆国では68℉と表現される。
摂氏温度と華氏温度の間には単純な関係があり,摂氏温度を1.8倍して32を加えれば華氏温度に変換できる。以下のRスクリプトで色々と試したりグラフ化したりすると良い。
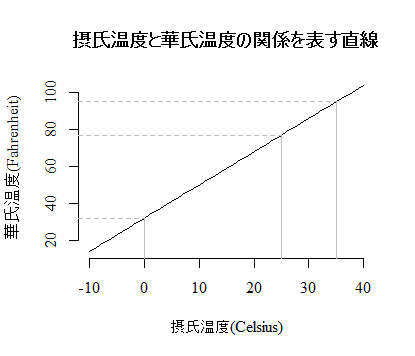
摂氏が10℃から20℃に2倍になっても,華氏は50℉から68℉であり,2倍にはならない。実際には気温や温度という同一のものを測定している筈なので,2倍であるか・2倍では無いかのいずれかの筈であるが,測定法によって2倍になったりならなかったりと云う事は,(少なくとも一方の測定法は)比例尺度では無いと云う事を意味する。
摂氏の0℃は華氏では32℉であり,0℉ではない。逆に華氏の0℉は摂氏の-17.78℃で0℃ではない。華氏も摂氏も0には実体的な意味がなく,或意味自由に定められている。こうした,0に実体的な・他の値とは質的に異なる意味が無い測定方法(単位)は,比例尺度では無い。
では温度を表す比例尺度は何かと云うと,「絶対温度または熱力学温度(K; Kelvin)」がそれである。熱力学温度は分子の平均運動エネルギーを表しており,熱力学温度が2倍になると云う事は含まれる熱エネルギーが2倍になる事に対応しており,正しく比例尺度と考える事が出来る。0Kを絶対零度とも呼ぶが,これは古典力学的には原子が運動を停止している状態を指し,実体的な意味を持つ。そして,通常の意味においては,負の絶対温度は存在しないとされる(現在の統計力学では,例外的に「負の絶対温度」と云う概念が存在するらしいが)。
間隔尺度か比率尺度かを簡単に見分ける一つのポイントは,自然に・素直にマイナスの値を考える事が出来るかどうか,と言えよう。長さのメートル,質量のグラムなどは,0というのは「そもそも長さ/重さが存在しない」と云う特別な意味を持ち,「或物の長さがマイナス1メートルである」と云った表現は,素直な・自然な理解が出来ないものである。こうした長さや重さの単位は比例尺度である。
もう一つ区別が難しい,と云うか特に社会調査において厳密には問題となるのが「順序尺度/間隔尺度」である。
社会調査・世論調査では,例えば,「『夫は外で働き,妻は家庭を守るべきである』という考え方について賛成ですか,反対ですか」との質問に対して,「1 賛成,2 どちらかといえば賛成,3 どちらともいえない,4 どちらかといえば反対,5 反対」の選択肢から一つを選んで貰う回答方式(5件法)がよくある。
この回答を,1〜5(もしくは逆順に5〜1)の数字に変換して,平均を計算したり,平均の男女差や世代差を計算したりする事がよくあるが,平均を計算すると云う事はこれを,単なる順序尺度ではなく間隔尺度と見做している事になる。間隔尺度だと見做すと云う事は,「1 賛成」と「2 どちらかといえば賛成」の差は,「2 どちらかといえば賛成」と「3 どちらともいえない」の差に等しく,「3 どちらともいえない」と「5 反対」の差の2倍であると考える事を意味する。
こうした計算に対して,「この回答・選択肢は,選択肢間の距離(賛否の強度の違い?)が等間隔であると前提する事は出来ず,順序尺度でしかない」とする批判もある。そうであれば,例えば,その1〜5の値をそのまま重回帰分析(第9章)の従属変数に使うと云った事は誤りである事になる。
回答選択肢としてはしばしば「3 どちらともいえない」が存在しない4件法も用いられる事を考えると,5件法の場合には1〜5の値で等間隔と見做し,4件法の場合には1〜4の値で等間隔と見做す事は確かに問題かも知れない。どちらかといえば賛成とどちらかといえば反対の間隔は,5件法では2になるが,4件法では1になってしまう。


しかし計量社会学では,こうした5件法(4件法)回答を間隔尺度扱いにして分析する習慣が長く存在している。必ずしもそれが認められないとは考えないが,議論の余地がある事は認識しておくのが良いだろう。因みに現在は,順序ロジット(第12章2-2)などのカテゴリカルデータ分析法が発達しているので,順序尺度のままで分析する事も十分に可能である。
よく見られる変数の分類法と測定尺度の関係を表に纏めてみる。表の上段ほど尺度水準が低く,言い換えれば含まれる情報量が少なく,表の下段ほど水準が高い,つまり含まれる情報量が多い。
| 4尺度水準 | 変数分類A | 変数分類B | 本書での提案 | ||
| 名義尺度 nominal | 質的変数 qualitative | カテゴリカル変数 | カテゴリカル変数 categorical | 名義尺度 | |
| 順序尺度 ordinal | 順序尺度 | ||||
| 間隔尺度 interval | 離散尺度 discrete | 量的変数 quantitative | 連続変数 | 数量変数 numerical | |
| 比例尺度 ratio | 連続尺度 continuous | ||||
「質的/量的」の二分法を使用しない理由については『入門・社会調査法〔第3版〕』第2章を参照して欲しい。
区別が難しい場合があるのは,「順序尺度/間隔尺度」と「間隔尺度/比例尺度」であるが,後者の「間隔尺度/比例尺度」については,本書のレヴェルでは無理して区別しなくても支障ない。
「間隔尺度/比例尺度」の区別の例としてよく見るのは,温度の単位の「摂氏温度℃」と「華氏温度℉」である。日本で20℃と表現する気温は,アメリカ合衆国では68℉と表現される。
摂氏温度と華氏温度の間には単純な関係があり,摂氏温度を1.8倍して32を加えれば華氏温度に変換できる。以下のRスクリプトで色々と試したりグラフ化したりすると良い。
# 摂氏温度(Celsius)から華氏温度(Fahrenheit)に変換
C <- 20.0 # 任意の摂氏温度を入力
F <- 1.8*C + 32; names(F) <- c("Fahrenheit"); names(C) <- c("Celsius")
C; F
# 華氏温度(Fahrenheit)から摂氏温度(Celsius)に変換
F <- 100.0 # 任意の華氏温度を入力
C <- 1/1.8*(F - 32); names(F) <- c("Fahrenheit"); names(C) <- c("Celsius")
F; C
# 摂氏を横軸,華氏を縦軸にしてグラフを書く
C <- -10:40 # 日本で比較的ありそうな気温の範囲に設定
F <- 1.8*C + 32
plot(C, F, bty="n", type="l", family="serif",
xlab="摂氏温度(Celsius)", ylab="華氏温度(Fahrenheit)",
main="摂氏温度と華氏温度の関係を表す直線")
segments(c(0, 25, 35), 0, c(0, 25, 35), 1.8*c(0, 25, 35)+32,
col="gray", lty=1)
segments(-12, 1.8*c(0, 25, 35)+32, c(0, 25, 35), 1.8*c(0, 25, 35)+32,
col="gray", lty=2)
C <- 20.0 # 任意の摂氏温度を入力
F <- 1.8*C + 32; names(F) <- c("Fahrenheit"); names(C) <- c("Celsius")
C; F
# 華氏温度(Fahrenheit)から摂氏温度(Celsius)に変換
F <- 100.0 # 任意の華氏温度を入力
C <- 1/1.8*(F - 32); names(F) <- c("Fahrenheit"); names(C) <- c("Celsius")
F; C
# 摂氏を横軸,華氏を縦軸にしてグラフを書く
C <- -10:40 # 日本で比較的ありそうな気温の範囲に設定
F <- 1.8*C + 32
plot(C, F, bty="n", type="l", family="serif",
xlab="摂氏温度(Celsius)", ylab="華氏温度(Fahrenheit)",
main="摂氏温度と華氏温度の関係を表す直線")
segments(c(0, 25, 35), 0, c(0, 25, 35), 1.8*c(0, 25, 35)+32,
col="gray", lty=1)
segments(-12, 1.8*c(0, 25, 35)+32, c(0, 25, 35), 1.8*c(0, 25, 35)+32,
col="gray", lty=2)

摂氏が10℃から20℃に2倍になっても,華氏は50℉から68℉であり,2倍にはならない。実際には気温や温度という同一のものを測定している筈なので,2倍であるか・2倍では無いかのいずれかの筈であるが,測定法によって2倍になったりならなかったりと云う事は,(少なくとも一方の測定法は)比例尺度では無いと云う事を意味する。
摂氏の0℃は華氏では32℉であり,0℉ではない。逆に華氏の0℉は摂氏の-17.78℃で0℃ではない。華氏も摂氏も0には実体的な意味がなく,或意味自由に定められている。こうした,0に実体的な・他の値とは質的に異なる意味が無い測定方法(単位)は,比例尺度では無い。
では温度を表す比例尺度は何かと云うと,「絶対温度または熱力学温度(K; Kelvin)」がそれである。熱力学温度は分子の平均運動エネルギーを表しており,熱力学温度が2倍になると云う事は含まれる熱エネルギーが2倍になる事に対応しており,正しく比例尺度と考える事が出来る。0Kを絶対零度とも呼ぶが,これは古典力学的には原子が運動を停止している状態を指し,実体的な意味を持つ。そして,通常の意味においては,負の絶対温度は存在しないとされる(現在の統計力学では,例外的に「負の絶対温度」と云う概念が存在するらしいが)。
間隔尺度か比率尺度かを簡単に見分ける一つのポイントは,自然に・素直にマイナスの値を考える事が出来るかどうか,と言えよう。長さのメートル,質量のグラムなどは,0というのは「そもそも長さ/重さが存在しない」と云う特別な意味を持ち,「或物の長さがマイナス1メートルである」と云った表現は,素直な・自然な理解が出来ないものである。こうした長さや重さの単位は比例尺度である。
もう一つ区別が難しい,と云うか特に社会調査において厳密には問題となるのが「順序尺度/間隔尺度」である。
社会調査・世論調査では,例えば,「『夫は外で働き,妻は家庭を守るべきである』という考え方について賛成ですか,反対ですか」との質問に対して,「1 賛成,2 どちらかといえば賛成,3 どちらともいえない,4 どちらかといえば反対,5 反対」の選択肢から一つを選んで貰う回答方式(5件法)がよくある。
この回答を,1〜5(もしくは逆順に5〜1)の数字に変換して,平均を計算したり,平均の男女差や世代差を計算したりする事がよくあるが,平均を計算すると云う事はこれを,単なる順序尺度ではなく間隔尺度と見做している事になる。間隔尺度だと見做すと云う事は,「1 賛成」と「2 どちらかといえば賛成」の差は,「2 どちらかといえば賛成」と「3 どちらともいえない」の差に等しく,「3 どちらともいえない」と「5 反対」の差の2倍であると考える事を意味する。
こうした計算に対して,「この回答・選択肢は,選択肢間の距離(賛否の強度の違い?)が等間隔であると前提する事は出来ず,順序尺度でしかない」とする批判もある。そうであれば,例えば,その1〜5の値をそのまま重回帰分析(第9章)の従属変数に使うと云った事は誤りである事になる。
回答選択肢としてはしばしば「3 どちらともいえない」が存在しない4件法も用いられる事を考えると,5件法の場合には1〜5の値で等間隔と見做し,4件法の場合には1〜4の値で等間隔と見做す事は確かに問題かも知れない。どちらかといえば賛成とどちらかといえば反対の間隔は,5件法では2になるが,4件法では1になってしまう。
「IT時代におけるくらしと社会に関する調査」(2014年10月,CAPI)より


しかし計量社会学では,こうした5件法(4件法)回答を間隔尺度扱いにして分析する習慣が長く存在している。必ずしもそれが認められないとは考えないが,議論の余地がある事は認識しておくのが良いだろう。因みに現在は,順序ロジット(第12章2-2)などのカテゴリカルデータ分析法が発達しているので,順序尺度のままで分析する事も十分に可能である。
1-2 代表値(中心傾向; central tendency)
本文で「xを変数のヴェクトルだとするとき」と書いているが,実際に演習できるように,模擬データを発生させてみよう。
このxに対して,データの個数,中央値,算術平均,そして最頻値を求める。(最頻値については若干の工夫が必要になる。)
本文同様,幾何平均,調和平均,トリム平均も求めてみよう。
通常の初歩的実習なら以上でも良いが,実践的な調査データの演習としては,欠損値(NA)が含まれていない点で単純であり,実際のデータの集計の際に躓くことになってしまう。よって上の変数xの中の値を幾つか NA に書き換えて同じことを試して欲しい。

面倒に思うだろうが,以下のように常にNAを意識して処理することになれるのが良い。
ポイントはデータの個数(ヴェクトルの長さ)を求める時にもNAを除外することを忘れないということであり,最初の length( )の中の"!"は否定を意味し,is.na(x) は「xのうちNAであるもの」を意味する。合わせて !is.na(x) で「xのうちNAではないもの」を意味するので,x[!is.na(x)] でxからNAではないものだけを抽出し,length(x[!is.na(x)]) でその個数(長さ)を求めている。

上ではあえていちいち length(x[!is.na(x)]) を書いたが,実際にはこれは n1 <- length(x[!is.na(x)]) などとしてオブジェクト(n1)に代入しておいて,このn1を必要なところで使用するのが良い。
n <- 125
x <- round(rnorm(n, mean=50, sd=10), 0)
取り敢えず今はこのコマンドの意味が分からなくても問題ない。演習用データとして変数(ヴェクトル)xが用意できたとだけ思っておけばよい。x <- round(rnorm(n, mean=50, sd=10), 0)
このxに対して,データの個数,中央値,算術平均,そして最頻値を求める。(最頻値については若干の工夫が必要になる。)
length(x) # データの個数
median(x) # 中央値
mean(x) # 算術平均
sum(x)/length(x) # 合計をデータの個数で割って算術平均を求める
table(x) # 最頻値を求める準備の為に,度数分布表の全体を表示
table(x)[table(x)==max(table(x))] # 度数分布表から最頻値だけ抜粋
【注意!】 この最後の一行は,テクスト本文で見ると長い等号が一つ("=")に見えますが,上記の通り半角の等号が二つ("==")です。御注意下さい。median(x) # 中央値
mean(x) # 算術平均
sum(x)/length(x) # 合計をデータの個数で割って算術平均を求める
table(x) # 最頻値を求める準備の為に,度数分布表の全体を表示
table(x)[table(x)==max(table(x))] # 度数分布表から最頻値だけ抜粋
本文同様,幾何平均,調和平均,トリム平均も求めてみよう。
prod(x)^(1/length(x)) # 幾何平均(相乗平均)?
exp(sum(log(x))/length(x)) # 幾何平均?
1/(sum(1/x)/length(x)) # 調和平均
mean(x, trim=0.05) # 10%トリム平均
exp(sum(log(x))/length(x)) # 幾何平均?
1/(sum(1/x)/length(x)) # 調和平均
mean(x, trim=0.05) # 10%トリム平均

通常の初歩的実習なら以上でも良いが,実践的な調査データの演習としては,欠損値(NA)が含まれていない点で単純であり,実際のデータの集計の際に躓くことになってしまう。よって上の変数xの中の値を幾つか NA に書き換えて同じことを試して欲しい。
x[seq(1, n, by=round(n/6, 0))] <- NA # xのうち6つくらいの値をNAに書き換える
x # 置換した結果を確認してみる
これで上の length( ), median( ), mean( ), sum( ), table( ), prod( )などを実行すると,length( )とtable( )以外は結果がNAになる。x # 置換した結果を確認してみる

面倒に思うだろうが,以下のように常にNAを意識して処理することになれるのが良い。
ポイントはデータの個数(ヴェクトルの長さ)を求める時にもNAを除外することを忘れないということであり,最初の length( )の中の"!"は否定を意味し,is.na(x) は「xのうちNAであるもの」を意味する。合わせて !is.na(x) で「xのうちNAではないもの」を意味するので,x[!is.na(x)] でxからNAではないものだけを抽出し,length(x[!is.na(x)]) でその個数(長さ)を求めている。
length(x[!is.na(x)]) # NAを除いたデータの個数
median(x, na.rm=T) # 中央値
mean(x, na.rm=T) # 算術平均
sum(x, na.rm=T)/length(x[!is.na(x)]) # 合計をデータの個数で割って算術平均を求める
table(x, useNA="ifany") # table( )では逆に,NAを省略させないことがしばしば重要
table(x)[table(x)==max(table(x))] # 最頻値にはNAは関係ないので省略して良い
prod(x, na.rm=T)^(1/length(x[!is.na(x)])) # 幾何平均(相乗平均)?
exp(sum(log(x), na.rm=T)/length(x[!is.na(x)])) # 幾何平均?
1/(sum(1/x, na.rm=T)/length(x[!is.na(x)])) # 調和平均
mean(x, trim=0.05, na.rm=T) # 10%トリム平均
median(x, na.rm=T) # 中央値
mean(x, na.rm=T) # 算術平均
sum(x, na.rm=T)/length(x[!is.na(x)]) # 合計をデータの個数で割って算術平均を求める
table(x, useNA="ifany") # table( )では逆に,NAを省略させないことがしばしば重要
table(x)[table(x)==max(table(x))] # 最頻値にはNAは関係ないので省略して良い
prod(x, na.rm=T)^(1/length(x[!is.na(x)])) # 幾何平均(相乗平均)?
exp(sum(log(x), na.rm=T)/length(x[!is.na(x)])) # 幾何平均?
1/(sum(1/x, na.rm=T)/length(x[!is.na(x)])) # 調和平均
mean(x, trim=0.05, na.rm=T) # 10%トリム平均

上ではあえていちいち length(x[!is.na(x)]) を書いたが,実際にはこれは n1 <- length(x[!is.na(x)]) などとしてオブジェクト(n1)に代入しておいて,このn1を必要なところで使用するのが良い。
1-3 偏差平方和(SS; Sum of Squares)と分散(variance)
1-4 標準偏差(standard deviation)
分散を求めるには var(x) とすればよい。しかし分散が何であるのかをより深く理解する為に,本文同様,var( )関数を用いずに分散を求めてみよう。
…(中略)…
…(中略)…

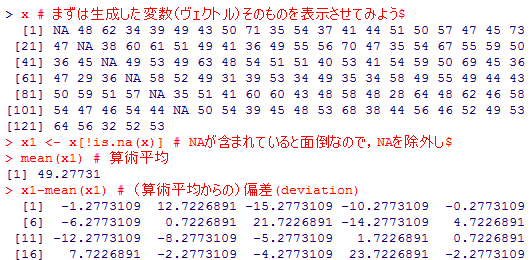
x # まずは生成した変数(ヴェクトル)そのものを表示させてみよう。
x1 <- x[!is.na(x)] # NAが含まれていると面倒なので,NAを除外したものを新たに x1 とする
mean(x1) # 算術平均
x1-mean(x1) # (算術平均からの)偏差(deviation)
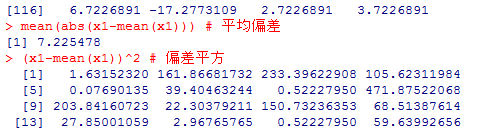
mean(abs(x1-mean(x1))) # 平均偏差
(x1-mean(x1))^2 # 偏差平方
sum((x1-mean(x1))^2) # 偏差平方和
sum((x1-mean(x1))^2)/length(x1) # 分散?
mean((x1-mean(x1))^2) # 分散?
var(x1) # Rの分散の関数.上の?や?とは一致しない.
sum((x1-mean(x1))^2)/(length(x1)-1) # 不偏分散
sqrt(mean((x1-mean(x1))^2)) # 標準偏差
sd(x1) # Rの標準偏差の関数.上とは一致しない.
sqrt(sum((x1-mean(x1))^2)/(length(x1)-1)) # 不偏分散の平方根
x1 <- x[!is.na(x)] # NAが含まれていると面倒なので,NAを除外したものを新たに x1 とする
mean(x1) # 算術平均
x1-mean(x1) # (算術平均からの)偏差(deviation)
mean(abs(x1-mean(x1))) # 平均偏差
(x1-mean(x1))^2 # 偏差平方
sum((x1-mean(x1))^2) # 偏差平方和
sum((x1-mean(x1))^2)/length(x1) # 分散?
mean((x1-mean(x1))^2) # 分散?
var(x1) # Rの分散の関数.上の?や?とは一致しない.
sum((x1-mean(x1))^2)/(length(x1)-1) # 不偏分散
sqrt(mean((x1-mean(x1))^2)) # 標準偏差
sd(x1) # Rの標準偏差の関数.上とは一致しない.
sqrt(sum((x1-mean(x1))^2)/(length(x1)-1)) # 不偏分散の平方根

…(中略)…

…(中略)…

2-1 カテゴリカル変数の度数分布表
今度は,カテゴリカル変数らしい模擬データを生成してみよう。本文2-1の表と,全く同じとはならないが,よく似た変数になるように工夫している。

(「編集」→「GUIプリファレンス」で "MS Gothic", size=10として描画。)
二つの dimnames( )関数は,値ラベルや表頭の列名を付けるものである。
t0からcp1までパーツを準備し,それを「列結合(cbind)」でひとまとめにしたのが ft0 である。
上記のスクリプトで,var1 <- var0 (本文で言えば var1 <- data$job)の代入式の右辺だけを変更すれば,任意の変数の度数分布表が同じスクリプトで作成できる。
var0 <- sample(c(1, 2, 3, 4, NA), size=384, replace=T,
prob=c(.474, .240, .099, .177, .010))
シンプルな度数分布表やそれを元にした集計を以下に示す。prob=c(.474, .240, .099, .177, .010))
table(var0) # シンプルな度数分布表
prop.table(table(var0)) # 比率に変換
cumsum(table(var0)) # 累積度数
本文2-1のような度数分布表を作成するスクリプトを以下で説明しよう。prop.table(table(var0)) # 比率に変換
cumsum(table(var0)) # 累積度数
var1 <- var0 # 集計したい変数をそのままvar1に代入。こうすることで汎用的スクリプトになる
t0 <- table(var1, useNA="always") # NAを含んだ総度数
dimnames(t0)[[1]] <- c("1 正規雇用","2 非正規雇用","3 自営","4 無職・学生","NA 欠損値")
t1 <- table(var1) # NAを除外した有効度数
p0 <- prop.table(t0) # NAを含んだ相対度数
ct0 <- cumsum(t0) # NAを含んだ累積度数
cp0 <- cumsum(p0) # NAを含んだ累積相対度数
p1 <- prop.table(t1) # 有効相対度数
cp1 <- cumsum(p1) # 累積有効相対度数
p1 <- c(p1, 0) # NAを含含むか含まないかによって行数が異なるので調整
cp1 <- c(cp1, 0) # NAの分行数が異なるので調整
ft0 <- cbind(t0, ct0, round(p0*100,1), round(cp0*100,1),
round(p1*100,1), round(cp1*100,1))
dimnames(ft0)[[2]] <- c("度数","累積度数","%","累積%", "有効%", "累積有効%")
ft0 # 最終的な度数分布表を表示
t0 <- table(var1, useNA="always") # NAを含んだ総度数
dimnames(t0)[[1]] <- c("1 正規雇用","2 非正規雇用","3 自営","4 無職・学生","NA 欠損値")
t1 <- table(var1) # NAを除外した有効度数
p0 <- prop.table(t0) # NAを含んだ相対度数
ct0 <- cumsum(t0) # NAを含んだ累積度数
cp0 <- cumsum(p0) # NAを含んだ累積相対度数
p1 <- prop.table(t1) # 有効相対度数
cp1 <- cumsum(p1) # 累積有効相対度数
p1 <- c(p1, 0) # NAを含含むか含まないかによって行数が異なるので調整
cp1 <- c(cp1, 0) # NAの分行数が異なるので調整
ft0 <- cbind(t0, ct0, round(p0*100,1), round(cp0*100,1),
round(p1*100,1), round(cp1*100,1))
dimnames(ft0)[[2]] <- c("度数","累積度数","%","累積%", "有効%", "累積有効%")
ft0 # 最終的な度数分布表を表示

(「編集」→「GUIプリファレンス」で "MS Gothic", size=10として描画。)
二つの dimnames( )関数は,値ラベルや表頭の列名を付けるものである。
t0からcp1までパーツを準備し,それを「列結合(cbind)」でひとまとめにしたのが ft0 である。
上記のスクリプトで,var1 <- var0 (本文で言えば var1 <- data$job)の代入式の右辺だけを変更すれば,任意の変数の度数分布表が同じスクリプトで作成できる。
2-2 1変量のグラフ表現
模擬データを生成して,ヒストグラムや箱ひげ図で図示してみよう。hist( )もboxplot( )もNAを除外して作図してくれるので,NAを含まない単純な模擬データで演習する。
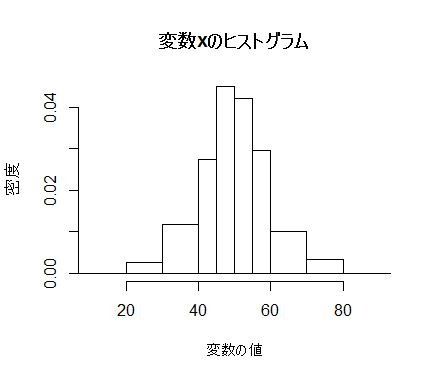
■ヒストグラム(histogram)
一つずつ試してみると,主なオプションの働きが分かるだろう。
■箱ひげ図(bos-and-whisker plot)
これも一つ一つ実行して,それぞれのオプションの意味を理解しよう。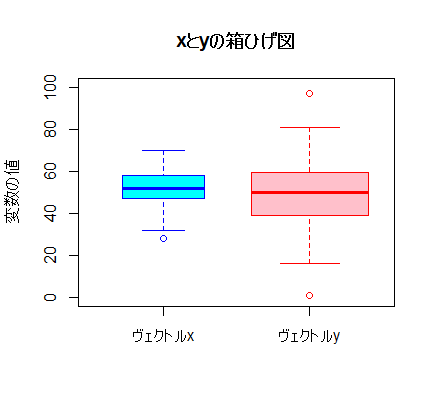
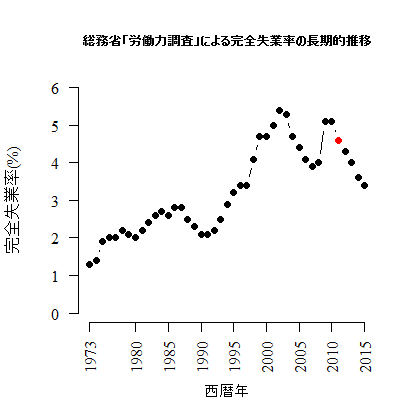
■折れ線グラフ(line graph)
時系列変化などを表すには折れ線グラフを用いる。ここでは,総務省の「労働力調査」の長期時系列データにおける「完全失業率」の年次変化をグラフ化してみる(長期時系列表2 就業状態別15歳以上人口−全国,列M: 完全失業率(%))。2011年の数値だけ他とは算出方法が異なるので色を変える。
■幹葉図(stem and leaf plot)
もう一つは幹葉図と呼ばれるものであるが,これは,テクスト(文字)のみで表現するのでグラフ機能を必要としない割には詳しい情報を表示すると云う利点がある一方で,データの数が多いと有効でなくなると云う欠点がある。ここでは,第3章1-2で使用する模擬年収データ(4,894人分)から200人分を無作為抽出して幹葉図で表現してみよう。比較のために同じデータをヒストグラムで描画する。

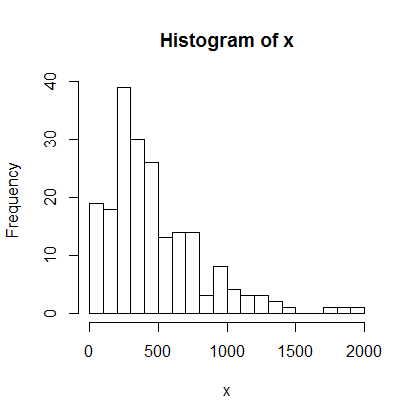
summary( )の結果やヒストグラムと比較して幹葉図を見ると読み取れると思うが,この例の場合には,年収の百万円以上の桁の部分がセパレータ(|)の左側(表側)に示され,その下の位である十万円の桁の数字が右側に昇順で羅列されている。
例えば, 10|4677 の行は,1040万円台が1名,1060万円台が1名,1070万円台が2名いる事を意味している。この様に一つ一つのケースを数字一つで表す為に,大量のデータの表示には向かない。
■ヒストグラム(histogram)
一つずつ試してみると,主なオプションの働きが分かるだろう。
x <- rnorm(n=400, mean=50, sd=10) # 模擬データ
hist(x) # 最も単純なヒストグラム
hist(x, xlim=c(10, 90), ylim=c(0, 100)) # x軸の範囲,y軸の範囲を指定
hist(x, xlim=c(10, 90), ylim=c(0, 100),
main="変数xのヒストグラム", xlab="変数の値", ylab="度数") # タイトルと軸ラベルを指定
hist(x, xlim=c(10, 90), ylim=c(0, 100),
main="変数xのヒストグラム", xlab="変数の値", ylab="度数",
breaks=seq(0, 100, by=5)) # x軸の区切り位置を指定
hist(x, xlim=c(10, 90), freq=F, # y軸を,度数ではなく密度に
main="変数xのヒストグラム", xlab="変数の値", ylab="密度",
breaks=seq(0, 100, by=5))
hist(x, xlim=c(10, 90), freq=F, # x軸の分割を不均等に,y軸は密度
main="変数xのヒストグラム", xlab="変数の値", ylab="密度",
breaks=c(0, 20, 30, 40, 45, 50, 55, 60, 70, 80, 100))
最後のものだけ以下に実例を示す〔歸山亜紀さん(群馬県立女子大学)に誤りを指摘して戴きました。2017.05.01〕。hist(x) # 最も単純なヒストグラム
hist(x, xlim=c(10, 90), ylim=c(0, 100)) # x軸の範囲,y軸の範囲を指定
hist(x, xlim=c(10, 90), ylim=c(0, 100),
main="変数xのヒストグラム", xlab="変数の値", ylab="度数") # タイトルと軸ラベルを指定
hist(x, xlim=c(10, 90), ylim=c(0, 100),
main="変数xのヒストグラム", xlab="変数の値", ylab="度数",
breaks=seq(0, 100, by=5)) # x軸の区切り位置を指定
hist(x, xlim=c(10, 90), freq=F, # y軸を,度数ではなく密度に
main="変数xのヒストグラム", xlab="変数の値", ylab="密度",
breaks=seq(0, 100, by=5))
hist(x, xlim=c(10, 90), freq=F, # x軸の分割を不均等に,y軸は密度
main="変数xのヒストグラム", xlab="変数の値", ylab="密度",
breaks=c(0, 20, 30, 40, 45, 50, 55, 60, 70, 80, 100))

■箱ひげ図(bos-and-whisker plot)
これも一つ一つ実行して,それぞれのオプションの意味を理解しよう。
x <- round(rnorm(n=100, mean=50, sd=10), 0)
y <- round(rnorm(n=200, mean=50, sd=15), 0) # ケース数と散布度の異なるヴェクトルを用意
boxplot(x) # 最も単純な箱ひげ図
boxplot(x, ylim=c(0, 100), # y軸の範囲を指定
main="xの箱ひげ図", ylab="変数の値") # タイトルとy軸ラベル
boxplot(x, y, ylim=c(0, 100), # 2つのヴェクトルを並べて図示
main="xとyの箱ひげ図", ylab="変数の値")
boxplot(x, y, ylim=c(0, 100),
main="xとyの箱ひげ図", ylab="変数の値",
names=c("ヴェクトルx", "ヴェクトルy")) # x軸にラベル
boxplot(x, y, ylim=c(0, 100), varwidth=T, # 幅がサンプルサイズの平方根に比例
main="xとyの箱ひげ図", ylab="変数の値",
names=c("ヴェクトルx", "ヴェクトルy"))
boxplot(x, y, ylim=c(0, 100), varwidth=T,
main="xとyの箱ひげ図", ylab="変数の値",
names=c("ヴェクトルx", "ヴェクトルy"),
col=c("cyan", "pink"), border=c("blue", "red")) # 色を付けてみた
y <- round(rnorm(n=200, mean=50, sd=15), 0) # ケース数と散布度の異なるヴェクトルを用意
boxplot(x) # 最も単純な箱ひげ図
boxplot(x, ylim=c(0, 100), # y軸の範囲を指定
main="xの箱ひげ図", ylab="変数の値") # タイトルとy軸ラベル
boxplot(x, y, ylim=c(0, 100), # 2つのヴェクトルを並べて図示
main="xとyの箱ひげ図", ylab="変数の値")
boxplot(x, y, ylim=c(0, 100),
main="xとyの箱ひげ図", ylab="変数の値",
names=c("ヴェクトルx", "ヴェクトルy")) # x軸にラベル
boxplot(x, y, ylim=c(0, 100), varwidth=T, # 幅がサンプルサイズの平方根に比例
main="xとyの箱ひげ図", ylab="変数の値",
names=c("ヴェクトルx", "ヴェクトルy"))
boxplot(x, y, ylim=c(0, 100), varwidth=T,
main="xとyの箱ひげ図", ylab="変数の値",
names=c("ヴェクトルx", "ヴェクトルy"),
col=c("cyan", "pink"), border=c("blue", "red")) # 色を付けてみた

折れ線グラフ(line graph),幹葉図(stem and leaf plot)
もう少し他の作図法も紹介しておこう。■折れ線グラフ(line graph)
時系列変化などを表すには折れ線グラフを用いる。ここでは,総務省の「労働力調査」の長期時系列データにおける「完全失業率」の年次変化をグラフ化してみる(長期時系列表2 就業状態別15歳以上人口−全国,列M: 完全失業率(%))。2011年の数値だけ他とは算出方法が異なるので色を変える。
year <- c(1973:2015)
unemployment <- c(1.3, 1.4, 1.9, 2.0, 2.0, 2.2, 2.1, 2.0, 2.2, 2.4, 2.6, 2.7, 2.6, 2.8, 2.8, 2.5, 2.3, 2.1, 2.1, 2.2, 2.5, 2.9, 3.2, 3.4, 3.4, 4.1, 4.7, 4.7, 5.0, 5.4, 5.3, 4.7, 4.4, 4.1, 3.9, 4.0, 5.1, 5.1, 4.6, 4.3, 4.0, 3.6, 3.4)
marker_col <- rep("black", length(year))
marker_col[year == 2011] <- c("red")
# 比較的シンプルなグラフ
plot(year, unemployment, bty="n", type="b", pch=16, col=marker_col)
# オプションなどを活用したグラフ
plot(year, unemployment, bty="n", type="b", pch=16, col=marker_col,
axes=F, family="serif", ylim=c(0, ceiling(max(unemployment))),
main="総務省「労働力調査」による完全失業率の長期的推移", xlab="西暦年",
ylab="完全失業率(%)", cex.main=0.8)
axis(side=1, at=c(1973, seq(1980, 2015, by=5)), family="serif", las=2)
axis(side=2, at=c(0:ceiling(max(unemployment))), family="serif", las=1)
スクリプトではシンプルなグラフとやや手を入れたグラフの二つが作成されているが,実例は後者のみ示しておく。unemployment <- c(1.3, 1.4, 1.9, 2.0, 2.0, 2.2, 2.1, 2.0, 2.2, 2.4, 2.6, 2.7, 2.6, 2.8, 2.8, 2.5, 2.3, 2.1, 2.1, 2.2, 2.5, 2.9, 3.2, 3.4, 3.4, 4.1, 4.7, 4.7, 5.0, 5.4, 5.3, 4.7, 4.4, 4.1, 3.9, 4.0, 5.1, 5.1, 4.6, 4.3, 4.0, 3.6, 3.4)
marker_col <- rep("black", length(year))
marker_col[year == 2011] <- c("red")
# 比較的シンプルなグラフ
plot(year, unemployment, bty="n", type="b", pch=16, col=marker_col)
# オプションなどを活用したグラフ
plot(year, unemployment, bty="n", type="b", pch=16, col=marker_col,
axes=F, family="serif", ylim=c(0, ceiling(max(unemployment))),
main="総務省「労働力調査」による完全失業率の長期的推移", xlab="西暦年",
ylab="完全失業率(%)", cex.main=0.8)
axis(side=1, at=c(1973, seq(1980, 2015, by=5)), family="serif", las=2)
axis(side=2, at=c(0:ceiling(max(unemployment))), family="serif", las=1)

■幹葉図(stem and leaf plot)
もう一つは幹葉図と呼ばれるものであるが,これは,テクスト(文字)のみで表現するのでグラフ機能を必要としない割には詳しい情報を表示すると云う利点がある一方で,データの数が多いと有効でなくなると云う欠点がある。ここでは,第3章1-2で使用する模擬年収データ(4,894人分)から200人分を無作為抽出して幹葉図で表現してみよう。比較のために同じデータをヒストグラムで描画する。
data02 <- read.csv("mock_income.csv")
# 個人年収100人分を無作為抽出(単位: 万円)
x <- sample(data02$income, 200, replace=F)
stem(x)
hist(x, breaks=seq(0, ceiling(max(x)/100)*100, by=100))
summary(x)
# 個人年収100人分を無作為抽出(単位: 万円)
x <- sample(data02$income, 200, replace=F)
stem(x)
hist(x, breaks=seq(0, ceiling(max(x)/100)*100, by=100))
summary(x)


summary( )の結果やヒストグラムと比較して幹葉図を見ると読み取れると思うが,この例の場合には,年収の百万円以上の桁の部分がセパレータ(|)の左側(表側)に示され,その下の位である十万円の桁の数字が右側に昇順で羅列されている。
例えば, 10|4677 の行は,1040万円台が1名,1060万円台が1名,1070万円台が2名いる事を意味している。この様に一つ一つのケースを数字一つで表す為に,大量のデータの表示には向かない。
3-1 正規分布(normal distribution)と標準正規分布(SND)
理論的な正規分布のグラフ描画については〈このページ〉で紹介しているので参照して欲しい。以下にその一部を微修正して紹介する。是非解読して試してほしい。
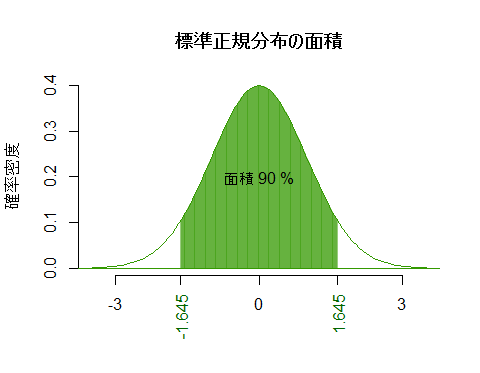
次は,x座標を指定すると,対応する面積を計算してグラフで示すスクリプト。
# 標準正規分布において,面積(%)を指定すると,対応するx座標を求めてグラフで示す
p <- .90 # ここは90%なら.90,95%なら.95,99%なら.99など,自分で好きに指定
q <- qnorm((1+p)/2, mean=0, sd=1)
curve(dnorm(x, mean=0, sd=1), from=-3.5, to=3.5,
bty="n", xaxp=c(-3, 3, 2),
xlab="", ylab="確率密度", main="標準正規分布の面積", col="#339900")
abline(h=0, col="#339900")
segments(x0 <- seq(-1*q, q, by=.01), 0, x0, dnorm(x0, 0, 1), col="#33990080")
axis(side=1, at=round(c(-1*q, q), 3), col.axis="#006600", cex=0.8, las=2)
text(0, 0.2, paste("面積", p*100, "%"))
p <- .90 # ここは90%なら.90,95%なら.95,99%なら.99など,自分で好きに指定
q <- qnorm((1+p)/2, mean=0, sd=1)
curve(dnorm(x, mean=0, sd=1), from=-3.5, to=3.5,
bty="n", xaxp=c(-3, 3, 2),
xlab="", ylab="確率密度", main="標準正規分布の面積", col="#339900")
abline(h=0, col="#339900")
segments(x0 <- seq(-1*q, q, by=.01), 0, x0, dnorm(x0, 0, 1), col="#33990080")
axis(side=1, at=round(c(-1*q, q), 3), col.axis="#006600", cex=0.8, las=2)
text(0, 0.2, paste("面積", p*100, "%"))

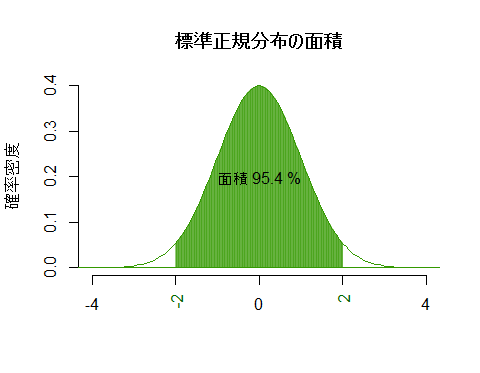
次は,x座標を指定すると,対応する面積を計算してグラフで示すスクリプト。
# 標準正規分布において,x座標を指定すると,対応する面積(%)を求めてグラフで示す
q <- 2.0 # x座標を,プラスの値で自分で好きに指定
p <- 1-(1-pnorm(q, mean=0, sd=1))*2
curve(dnorm(x, mean=0, sd=1), from=-4, to=4,
bty="n", xaxp=c(-4, 4, 2),
xlab="", ylab="確率密度", main="標準正規分布の面積", col="#339900")
abline(h=0, col="#339900")
segments(x0 <- seq(-1*q, q, by=.01), 0, x0, dnorm(x0, 0, 1), col="#33990080")
axis(side=1, at=round(c(-1*q, q), 3), col.axis="#006600", cex=0.8, las=2)
text(0, 0.2, paste("面積", round(p*100, 1), "%"))
q <- 2.0 # x座標を,プラスの値で自分で好きに指定
p <- 1-(1-pnorm(q, mean=0, sd=1))*2
curve(dnorm(x, mean=0, sd=1), from=-4, to=4,
bty="n", xaxp=c(-4, 4, 2),
xlab="", ylab="確率密度", main="標準正規分布の面積", col="#339900")
abline(h=0, col="#339900")
segments(x0 <- seq(-1*q, q, by=.01), 0, x0, dnorm(x0, 0, 1), col="#33990080")
axis(side=1, at=round(c(-1*q, q), 3), col.axis="#006600", cex=0.8, las=2)
text(0, 0.2, paste("面積", round(p*100, 1), "%"))

3-2 変数の標準化(standardization)
ここでは,試験の点数を模した模擬データを発生させて,それを標準化して標準化スコアを求め,更に受験業界でよく知られている「偏差値」に換算して比較してみよう(素点を発生させる部分は試行錯誤で余計な工夫をしているので余り気にしなくて良い)。
まずはそれぞれの要約統計量をsummary( )関数で表示させているので自分で試してみて欲しい。

その次に,それぞれのヒストグラム3つを横に並べて描いている。以下にその試行例を一枚示す。乱数を使用しているので変数発生を行う度に変化する。
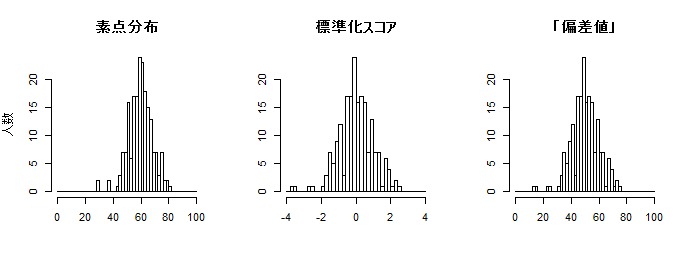
尚,元の変数が正規分布ではない限り,標準化スコアも正規分布にはならない。標準化すれば必ず「平均が0に,分散と標準偏差が1に」なるが,標準正規分布になるかどうかは,元の変数が正規分布かどうかに依存する。上のスクリプトの score <- の行だけを例えば score <- runif(n, min=30, max=80) と書き換えて試してみるとはっきりするだろう(以下にヒストグラムのみ例示)。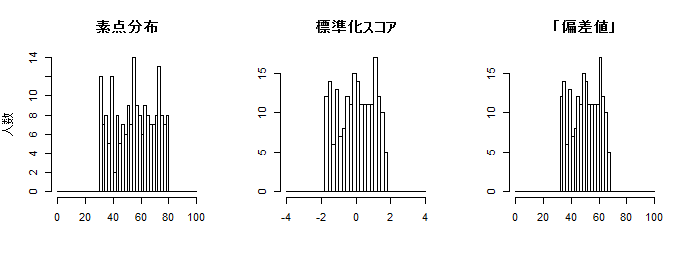
n <- 200 # 取り敢えず200人分とする
score <- rbinom(n, size=300, prob=.65)-135 # それっぽい素点の生成を工夫
score[score < 0] <- 0 # 念の為の処理
score[score > 100] <- 100 # 念の為の処理
z <- scale(score) # scale( )関数を使用して標準化
Z <- 10 * z + 50 # 標準化スコアから,「偏差値」を換算
summary(score) # 素点
summary(z) # 標準化スコア
summary(Z) # 「偏差値」
par(mfrow=c(1, 3)) # グラフを3枚横に並べる為の指示
hist(score, breaks=seq(0, 100, by=2), main="素点分布", ylab="人数", xlab="")
hist(z, breaks=seq(-4, 4, by=.2), main="標準化スコア", ylab="", xlab="")
hist(Z, breaks=seq(0, 100, by=2), main="「偏差値」", ylab="", xlab="")
スクリプトに#でコメントを付けてある様に,0点から100点の間の点数をn=200人分発生させ,それを標準化したzを求め,更にそこからいわゆる「偏差値」に換算したZを求めている。score <- rbinom(n, size=300, prob=.65)-135 # それっぽい素点の生成を工夫
score[score < 0] <- 0 # 念の為の処理
score[score > 100] <- 100 # 念の為の処理
z <- scale(score) # scale( )関数を使用して標準化
Z <- 10 * z + 50 # 標準化スコアから,「偏差値」を換算
summary(score) # 素点
summary(z) # 標準化スコア
summary(Z) # 「偏差値」
par(mfrow=c(1, 3)) # グラフを3枚横に並べる為の指示
hist(score, breaks=seq(0, 100, by=2), main="素点分布", ylab="人数", xlab="")
hist(z, breaks=seq(-4, 4, by=.2), main="標準化スコア", ylab="", xlab="")
hist(Z, breaks=seq(0, 100, by=2), main="「偏差値」", ylab="", xlab="")
まずはそれぞれの要約統計量をsummary( )関数で表示させているので自分で試してみて欲しい。

その次に,それぞれのヒストグラム3つを横に並べて描いている。以下にその試行例を一枚示す。乱数を使用しているので変数発生を行う度に変化する。

尚,元の変数が正規分布ではない限り,標準化スコアも正規分布にはならない。標準化すれば必ず「平均が0に,分散と標準偏差が1に」なるが,標準正規分布になるかどうかは,元の変数が正規分布かどうかに依存する。上のスクリプトの score <- の行だけを例えば score <- runif(n, min=30, max=80) と書き換えて試してみるとはっきりするだろう(以下にヒストグラムのみ例示)。

発展1-1 分散と不偏分散(unbiased variance)
人為的に発生させたデータについて,標本分散・標本標準偏差を定義式に従って求め,次にRの関数var( ),sd( )の結果と比べてみる。

定義式に従った標本分散はRの関数var( )の結果とは一致しない事,nではなくn-1で割った不偏分散がvar( )の結果と一致する事,当然ながら不偏分散の方が標本分散よりも少し大きな値になる事,を確認しよう。
n=50の場合は,50/49=1.020408で,不偏分散の方が2%程度大きくなるが,n=500になるとこれが0.2%の違いでしかなくなるので,実際の計算上はそれ程神経質にならなくても良い。ケース数が小さい時には注意しよう。
n <- 50
x <- rnorm(n, mean=50, sd=10) # データの生成
# 平均からの偏差: x - mean(x)
# 偏差平方: (x - mean(x))^2
sum((x - mean(x))^2) # 偏差平方和
sum((x - mean(x))^2)/n # 定義式に従った標本分散
mean((x - mean(x))^2) # 偏差平方の平均=標本分散
sqrt(mean((x - mean(x))^2)) # 標本標準偏差
# Rの分散var( ),標準偏差sd( )
var(x); sd(x)
# 定義式に従った不偏分散
sum((x - mean(x))^2)/(n-1)
x <- rnorm(n, mean=50, sd=10) # データの生成
# 平均からの偏差: x - mean(x)
# 偏差平方: (x - mean(x))^2
sum((x - mean(x))^2) # 偏差平方和
sum((x - mean(x))^2)/n # 定義式に従った標本分散
mean((x - mean(x))^2) # 偏差平方の平均=標本分散
sqrt(mean((x - mean(x))^2)) # 標本標準偏差
# Rの分散var( ),標準偏差sd( )
var(x); sd(x)
# 定義式に従った不偏分散
sum((x - mean(x))^2)/(n-1)

定義式に従った標本分散はRの関数var( )の結果とは一致しない事,nではなくn-1で割った不偏分散がvar( )の結果と一致する事,当然ながら不偏分散の方が標本分散よりも少し大きな値になる事,を確認しよう。
n=50の場合は,50/49=1.020408で,不偏分散の方が2%程度大きくなるが,n=500になるとこれが0.2%の違いでしかなくなるので,実際の計算上はそれ程神経質にならなくても良い。ケース数が小さい時には注意しよう。
発展1-2 最小二乗和推定量としての算術平均
これも,模擬データを発生させて,代表値wからの偏差平方和が最小になるのが,wが算術平均である時である事を示してみよう。

スクリプトを解読する事は未だ難しいかも知れないが,最終的に誤差平方和の最小値,その時のwの値,実際の算術平均と偏差平方和を見比べて,一致している事を確認して欲しい。
n <- 100
x <- round(rnorm(n, mean=50, sd=15), 0) # 整数データの生成
# 最小値から最大値までの範囲で0.1刻みのヴェクトルを準備
w <- seq(min(x), max(x), by=.1)
L <- length(w) # ヴェクトルwの長さ(=数字の個数)をLとする
LS <- numeric(L) # Lだけ数字を格納出来る空のヴェクトルLSを準備する
# iからLまでiの値を一つずつ増やしつつ,あるwからの偏差の平方の合計(誤差平方和)を格納
for (i in 1:L) {
LS[i] <- sum((x - w[i])^2)
}
min(LS) # 誤差平方和の最小値(=最小二乗和)
w[LS == min(LS)] # 誤差平方和が最小になる時のwの値
mean(x) # 実際のxの算術平均
var(x)*(n-1) # 実際のxの偏差平方和
x <- round(rnorm(n, mean=50, sd=15), 0) # 整数データの生成
# 最小値から最大値までの範囲で0.1刻みのヴェクトルを準備
w <- seq(min(x), max(x), by=.1)
L <- length(w) # ヴェクトルwの長さ(=数字の個数)をLとする
LS <- numeric(L) # Lだけ数字を格納出来る空のヴェクトルLSを準備する
# iからLまでiの値を一つずつ増やしつつ,あるwからの偏差の平方の合計(誤差平方和)を格納
for (i in 1:L) {
LS[i] <- sum((x - w[i])^2)
}
min(LS) # 誤差平方和の最小値(=最小二乗和)
w[LS == min(LS)] # 誤差平方和が最小になる時のwの値
mean(x) # 実際のxの算術平均
var(x)*(n-1) # 実際のxの偏差平方和

スクリプトを解読する事は未だ難しいかも知れないが,最終的に誤差平方和の最小値,その時のwの値,実際の算術平均と偏差平方和を見比べて,一致している事を確認して欲しい。
発展1-3 Rにおける欠損値(missing value)
Rで実際の調査データを扱い始めた途端に困るのが,実際のデータには欠損値(missing)が含まれている事である。Rの入門的解説では,取り敢えず欠損値を度外視して説明している場合が多く,其の儘では使えなくなって困ってしまう事が多い。かなり面倒には感じるが,学習者は常に欠損値について処置しなければならない場合が多いと云う事を念頭においておこう。集計や分析をしていて「何か変だな?」と感じたら必ず「NAはきちんと扱われているかな?」と気にかけよう。
以下に,スクリプトに#コメントを付けたので,自分でも実際に試しながらよく理解しよう。結果は二つに分けて掲示する。

次は2変数の分割表(クロス表)で例示する。いずれか一方にNAが含まれるケースはデフォルトでは全て除外される事,useNA="always"を付けると実際にはNAが無くても分割表にNAの欄が明示される事を確認しよう。

最初に度数分布表や分割表を出力する場合には必ずuseNA="always"またはuseNA="ifany"として確認する習慣をつけておくのが良い。
以下に,スクリプトに#コメントを付けたので,自分でも実際に試しながらよく理解しよう。結果は二つに分けて掲示する。
x <- c(1, 2, 3, 4, 5, 6, 7, NA, 8, 9, 10)
mean(x); median(x); sd(x); sum(x) # いずれもNAは不可
summary(x) # NAを含んでも可
length(x) # NAも含んだ数字の個数を出力する
mean(x, na.rm=TRUE) # NA を除外して算術平均を計算。 NA を remove する。
median(x, na.rm=T) # TRUE は T と略する事が出来る。
var(x, na.rm=T); sd(x, na.rm=T)
table(x) # NAは自動的に除外
table(x, useNA="ifany") # NAがあるかどうかに注意
y <- c(1, 1, 1, 2, 2, 3, 3, NA)
z <- c(7, NA, 5, 6, 7, 6, 5, 7)
table(y, z) # いずれか一方にでも NA があると除外
table(y, z, useNA="ifany") # 「もしNAがあれば含めよ」とのオプション
y1 <- y[complete.cases(y, z)] # いずれもNAでないものだけ
z1 <- z[complete.cases(y, z)]
y1; z1
table(y1, z1, useNA="always") # NAがあろうがなかろうが表示
特に table( )関数の様に,自動で削除する関数の場合は,ユーザはNAの事を忘れがちになるのでしばしば注意が必要である。mean(x); median(x); sd(x); sum(x) # いずれもNAは不可
summary(x) # NAを含んでも可
length(x) # NAも含んだ数字の個数を出力する
mean(x, na.rm=TRUE) # NA を除外して算術平均を計算。 NA を remove する。
median(x, na.rm=T) # TRUE は T と略する事が出来る。
var(x, na.rm=T); sd(x, na.rm=T)
table(x) # NAは自動的に除外
table(x, useNA="ifany") # NAがあるかどうかに注意
y <- c(1, 1, 1, 2, 2, 3, 3, NA)
z <- c(7, NA, 5, 6, 7, 6, 5, 7)
table(y, z) # いずれか一方にでも NA があると除外
table(y, z, useNA="ifany") # 「もしNAがあれば含めよ」とのオプション
y1 <- y[complete.cases(y, z)] # いずれもNAでないものだけ
z1 <- z[complete.cases(y, z)]
y1; z1
table(y1, z1, useNA="always") # NAがあろうがなかろうが表示

次は2変数の分割表(クロス表)で例示する。いずれか一方にNAが含まれるケースはデフォルトでは全て除外される事,useNA="always"を付けると実際にはNAが無くても分割表にNAの欄が明示される事を確認しよう。

最初に度数分布表や分割表を出力する場合には必ずuseNA="always"またはuseNA="ifany"として確認する習慣をつけておくのが良い。
第1章の【練習問題】の解答
Copyright (C) 2016-2017 SUGINO Isamu All Rights Reserved. design by tempnate



