杉野 勇 (SUGINO Isamu) お茶の水女子大学・人間発達科学専攻・応用社会学コース担当
『入門・社会統計学』サポートウェブ |
|
 第10章 重回帰分析(?)
第10章 重回帰分析(?)
1-1 二乗項(squared term)
本文の例を,サポートウェブの表記や流儀に合わせて実行してみよう。
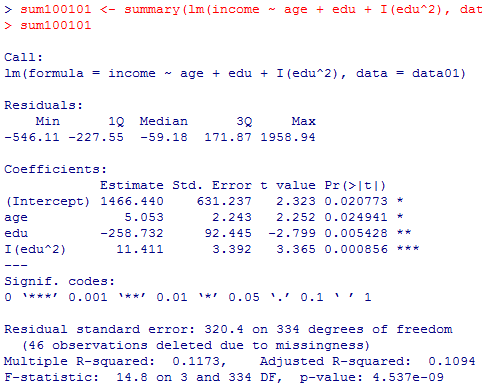
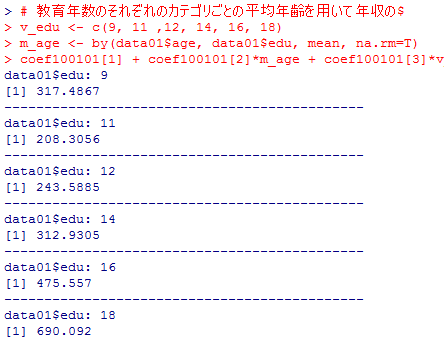
教育年数eduの1次の項も二次の項も1%水準で有意なので,教育年数は個人年収に対して非線形の(曲線的な)関係を有していると考えられる。その下に凸な放物線の頂点のx座標を求めると,
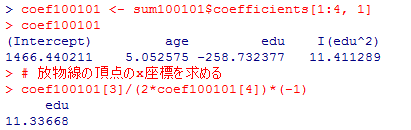
単純に直線的に上昇しないのが不思議に思われるだろうが,データの中に専修学校高等課程(教育年数11年として計算)の回答者がわずかに含まれ,この人たちの平均年収が中卒や高卒以上の人達と比べてかなり低いためにこうした結果になっている。ケース数や教育年数カテゴリ別平均年収を確認してみよう。
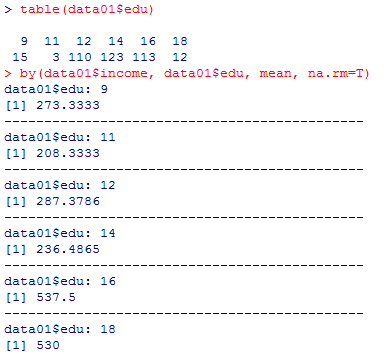
因みに,それぞれの教育年数グループで平均年齢が異なるのでグループごとの平均年齢を用いて予測値を求めると,317万円,208万円,244万円,313万円,476万円,690万円となる。
sum100101 <- summary(lm(income ~ age + edu + I(edu^2), data=data01))
sum100101
sum100101

教育年数eduの1次の項も二次の項も1%水準で有意なので,教育年数は個人年収に対して非線形の(曲線的な)関係を有していると考えられる。その下に凸な放物線の頂点のx座標を求めると,
coef100101 <- sum100101$coefficients[1:4, 1]
coef100101
# 放物線の頂点のx座標を求める
coef100101[3]/(2*coef100101[4])*(-1)
coef100101
# 放物線の頂点のx座標を求める
coef100101[3]/(2*coef100101[4])*(-1)

単純に直線的に上昇しないのが不思議に思われるだろうが,データの中に専修学校高等課程(教育年数11年として計算)の回答者がわずかに含まれ,この人たちの平均年収が中卒や高卒以上の人達と比べてかなり低いためにこうした結果になっている。ケース数や教育年数カテゴリ別平均年収を確認してみよう。

因みに,それぞれの教育年数グループで平均年齢が異なるのでグループごとの平均年齢を用いて予測値を求めると,317万円,208万円,244万円,313万円,476万円,690万円となる。
# 教育年数のそれぞれのカテゴリごとの平均年齢を用いて年収の予測値を計算する
v_edu <- c(9, 11 ,12, 14, 16, 18)
m_age <- by(data01$age, data01$edu, mean, na.rm=T)
coef100101[1] + coef100101[2]*m_age + coef100101[3]*v_edu + coef100101[4]*v_edu^2
v_edu <- c(9, 11 ,12, 14, 16, 18)
m_age <- by(data01$age, data01$edu, mean, na.rm=T)
coef100101[1] + coef100101[2]*m_age + coef100101[3]*v_edu + coef100101[4]*v_edu^2

1-2 交互作用項(interaction term)
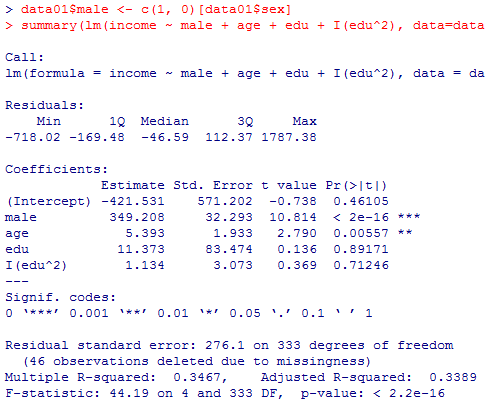
本文では,男性ダミーの主効果を投入して個人年収を説明する重回帰分析で,教育年数は二乗項のみを入れている。その理由も含めて以下に結果を示す。
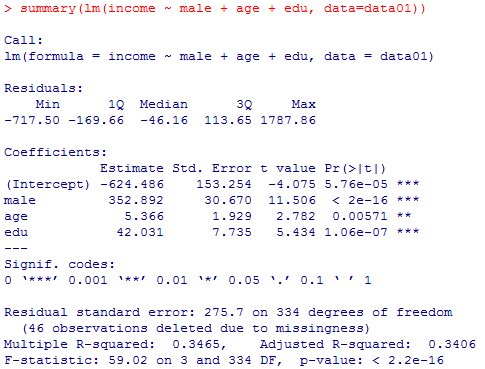
教育年数の一次の項と二次の項を同時投入するといずれも有意にならず,分散説明率は.3467(自由度調整済みで.3389)である。教育年数の一次の項のみだと.3465(.3406),二次の項のみだと.3467(.3408)。よって,僅かではあるが二乗項のみの投入が最善である。
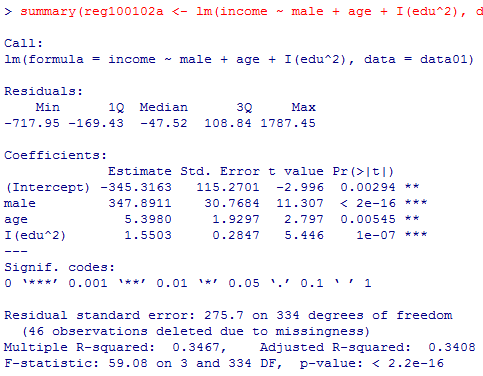
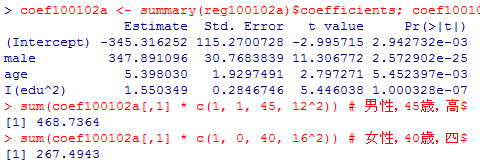
この結果から幾つかのパタンについて予測値を計算してみよう。
次に,性別と年齢の交互作用を投入した重回帰分析の結果である。
これについて上と同じパタンで予測値を求めてみる。ただし,定数項,男性ダミー主効果,年齢主効果は10%水準でも有意ではない(=0でないとは言えない)ので,計算には含めない。
全く有意にならなかった年齢主効果,男性ダミー主効果を除去したモデルも確認してみよう。
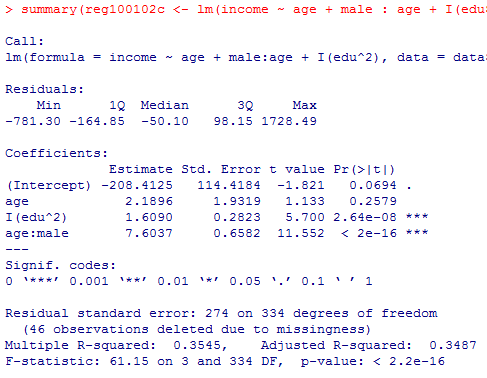
自由度調整済み分散説明率(Adjusted R-squared)に着目すると,本文でも採用している最後のモデルが僅かに良い値である。しかし本文脚注で述べた様に,モデル選択において用いられる基準であるAIC(赤池情報量規準)やBIC(ベイズ情報量規準)を計算すると,年齢と男性ダミーの双方の主効果を除去したモデルが最も良好となる。

本文の,世帯収入を説明する重回帰分析を行う。教育年数の二乗項を入れないのは,予備的に分析した結果,二乗項を投入するよりも一次の項を投入した方が僅かに良好だった為である。
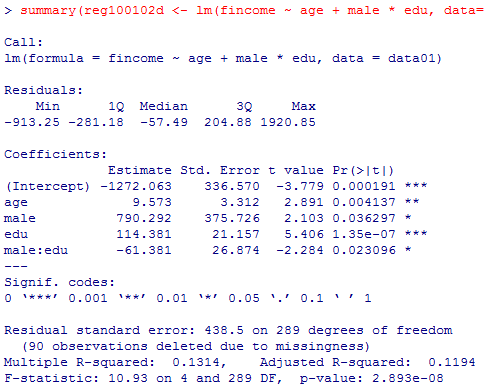
全ての係数が有意であるが,本文でも書いた通り,ダミー変数,それも交互作用を含む場合には,ダミー変数の値によって予測式を書き分けた方がきちんと理解出来る。
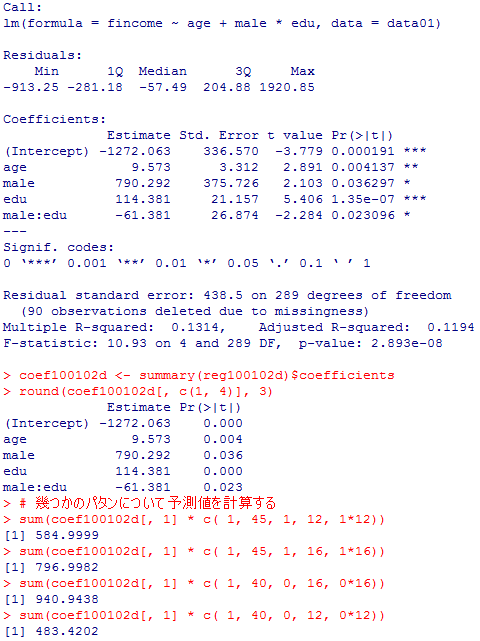
教育年数の一次の項と二次の項を同時投入するといずれも有意にならず,分散説明率は.3467(自由度調整済みで.3389)である。教育年数の一次の項のみだと.3465(.3406),二次の項のみだと.3467(.3408)。よって,僅かではあるが二乗項のみの投入が最善である。
data01$male <- c(1, 0)[data01$sex]
summary(lm(income ~ male + age + edu + I(edu^2), data=data01))
summary(lm(income ~ male + age + edu, data=data01))
summary(reg100102a <- lm(income ~ male + age + I(edu^2), data=data01))
summary(lm(income ~ male + age + edu + I(edu^2), data=data01))
summary(lm(income ~ male + age + edu, data=data01))
summary(reg100102a <- lm(income ~ male + age + I(edu^2), data=data01))



この結果から幾つかのパタンについて予測値を計算してみよう。
coef100102a <- summary(reg100102a)$coefficients; coef100102a
sum(coef100102a[,1] * c(1, 1, 45, 12^2)) # 男性,45歳,高校卒
sum(coef100102a[,1] * c(1, 0, 40, 16^2)) # 女性,40歳,四大卒
sum(coef100102a[,1] * c(1, 1, 45, 12^2)) # 男性,45歳,高校卒
sum(coef100102a[,1] * c(1, 0, 40, 16^2)) # 女性,40歳,四大卒

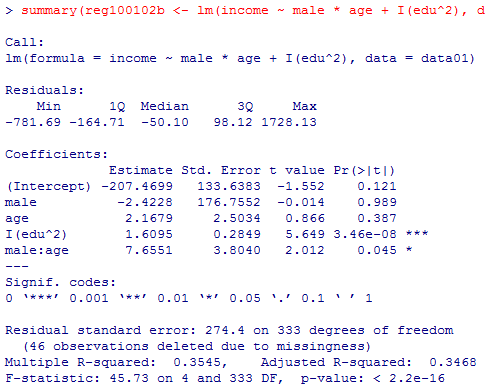
次に,性別と年齢の交互作用を投入した重回帰分析の結果である。
summary(reg100102b <- lm(income ~ male * age + I(edu^2), data=data01))
# male * age は male + age + male:age でも同じ
# male * age は male + age + male:age でも同じ

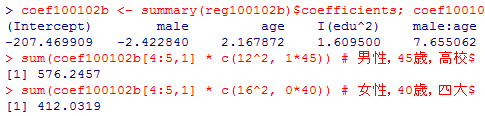
これについて上と同じパタンで予測値を求めてみる。ただし,定数項,男性ダミー主効果,年齢主効果は10%水準でも有意ではない(=0でないとは言えない)ので,計算には含めない。
coef100102b <- summary(reg100102b)$coefficients; coef100102b[,1]
sum(coef100102b[4:5,1] * c(12^2, 1*45)) # 男性,45歳,高校卒
sum(coef100102b[4:5,1] * c(16^2, 0*40)) # 女性,40歳,四大卒
sum(coef100102b[4:5,1] * c(12^2, 1*45)) # 男性,45歳,高校卒
sum(coef100102b[4:5,1] * c(16^2, 0*40)) # 女性,40歳,四大卒

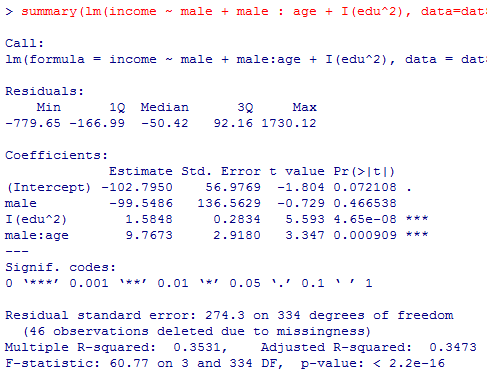
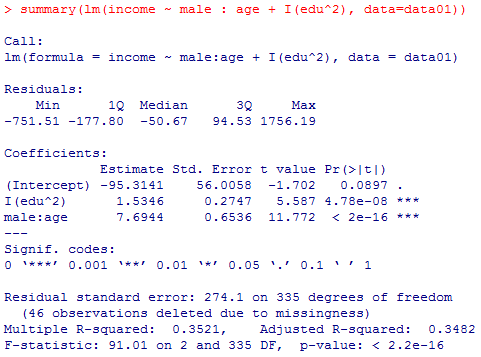
全く有意にならなかった年齢主効果,男性ダミー主効果を除去したモデルも確認してみよう。
summary(lm(income ~ male + male : age + I(edu^2), data=data01))
summary(lm(income ~ male : age + I(edu^2), data=data01))
summary(reg100102c <- lm(income ~ age + male : age + I(edu^2), data=data01))
summary(lm(income ~ male : age + I(edu^2), data=data01))
summary(reg100102c <- lm(income ~ age + male : age + I(edu^2), data=data01))



自由度調整済み分散説明率(Adjusted R-squared)に着目すると,本文でも採用している最後のモデルが僅かに良い値である。しかし本文脚注で述べた様に,モデル選択において用いられる基準であるAIC(赤池情報量規準)やBIC(ベイズ情報量規準)を計算すると,年齢と男性ダミーの双方の主効果を除去したモデルが最も良好となる。

本文の,世帯収入を説明する重回帰分析を行う。教育年数の二乗項を入れないのは,予備的に分析した結果,二乗項を投入するよりも一次の項を投入した方が僅かに良好だった為である。
summary(reg100102d <- lm(fincome ~ age + male * edu, data=data01))

全ての係数が有意であるが,本文でも書いた通り,ダミー変数,それも交互作用を含む場合には,ダミー変数の値によって予測式を書き分けた方がきちんと理解出来る。
summary(reg100102d <- lm(fincome ~ age + male * edu, data=data01))
coef100102d <- summary(reg100102d)$coefficients
round(coef100102d[, c(1, 4)], 3)
# 幾つかのパタンについて予測値を計算する
sum(coef100102d[, 1] * c( 1, 45, 1, 12, 1*12))
sum(coef100102d[, 1] * c( 1, 45, 1, 16, 1*16))
sum(coef100102d[, 1] * c( 1, 40, 0, 16, 0*16))
sum(coef100102d[, 1] * c( 1, 40, 0, 12, 0*12))
coef100102d <- summary(reg100102d)$coefficients
round(coef100102d[, c(1, 4)], 3)
# 幾つかのパタンについて予測値を計算する
sum(coef100102d[, 1] * c( 1, 45, 1, 12, 1*12))
sum(coef100102d[, 1] * c( 1, 45, 1, 16, 1*16))
sum(coef100102d[, 1] * c( 1, 40, 0, 16, 0*16))
sum(coef100102d[, 1] * c( 1, 40, 0, 12, 0*12))

1-3 多重共線性(multicollinearity)
本文と同様の重回帰分析を行って,toleranceやvifを計算してみよう。

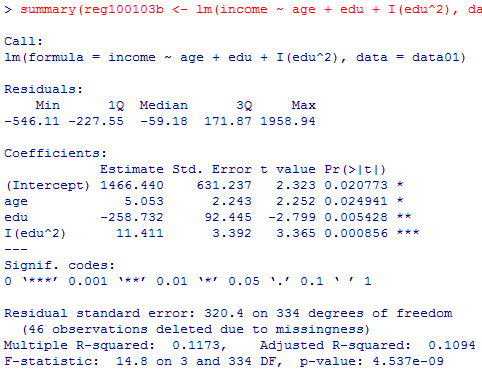
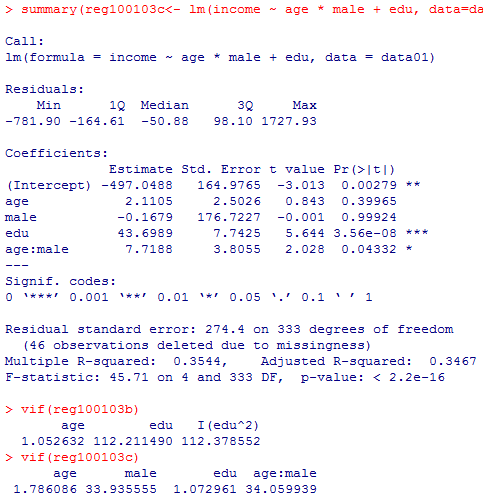
モデルreg100103bについては,標準誤差が著しく大きくなってt検定が有意にならないという問題は生じていない。モデルreg100103cでは特にmaleの主効果で標準誤差が著しく大きいので,これを独立変数から除外しても良いかも知れない。
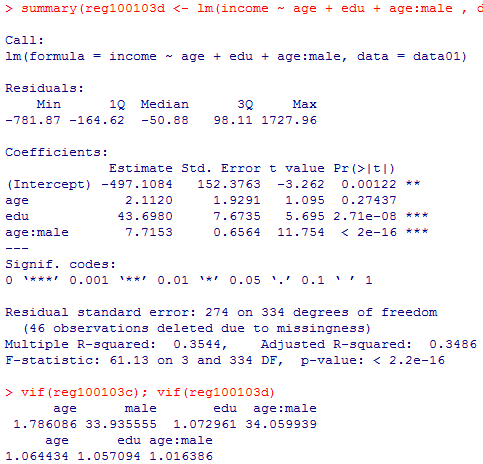
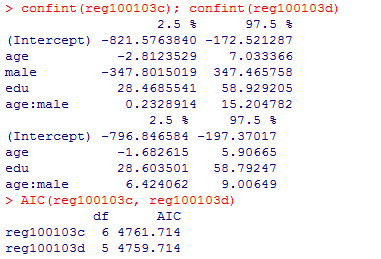
maleの主効果を除外したモデルreg100103dを計算すると,先のモデルreg100103cよりも,定数項を含むそれぞれの要因の標準誤差が小さくなって信頼区間が狭くなり,自由度調整済み分散説明率は上昇し,赤池情報量基準AICは低下するというように,すべての指標においてreg100103dのほうが優れている。

library(car)
summary(reg100103a <- lm(income ~ age + male + edu, data=data01))
vif(reg100103a)
1/vif(reg100103a) # これがトレランスの値
summary(reg100103a <- lm(income ~ age + male + edu, data=data01))
vif(reg100103a)
1/vif(reg100103a) # これがトレランスの値

summary(reg100103b <- lm(income ~ age + edu + I(edu^2), data=data01))
summary(reg100103c<- lm(income ~ age * male + edu, data=data01))
vif(reg100103b)
vif(reg100103c)
summary(reg100103c<- lm(income ~ age * male + edu, data=data01))
vif(reg100103b)
vif(reg100103c)


モデルreg100103bについては,標準誤差が著しく大きくなってt検定が有意にならないという問題は生じていない。モデルreg100103cでは特にmaleの主効果で標準誤差が著しく大きいので,これを独立変数から除外しても良いかも知れない。
summary(reg100103c <- lm(income ~ age * male + edu, data=data01))
summary(reg100103d <- lm(income ~ age + edu + age:male , data=data01))
vif(reg100103c); vif(reg100103d)
confint(reg100103c); confint(reg100103d)
AIC(reg100103c, reg100103d)
summary(reg100103d <- lm(income ~ age + edu + age:male , data=data01))
vif(reg100103c); vif(reg100103d)
confint(reg100103c); confint(reg100103d)
AIC(reg100103c, reg100103d)


maleの主効果を除外したモデルreg100103dを計算すると,先のモデルreg100103cよりも,定数項を含むそれぞれの要因の標準誤差が小さくなって信頼区間が狭くなり,自由度調整済み分散説明率は上昇し,赤池情報量基準AICは低下するというように,すべての指標においてreg100103dのほうが優れている。
定義に従ったVIFの計算
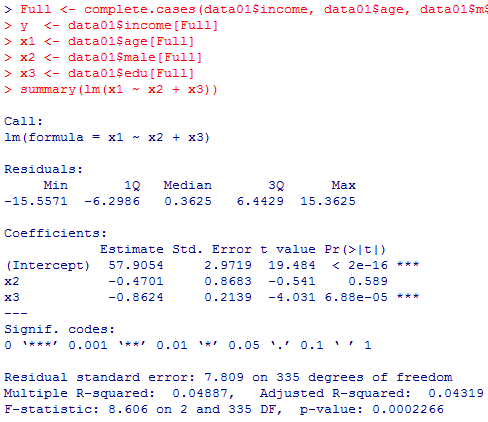
本文で触れた,carパッケイジを使わずにvifを計算する方法を紹介しておく。本項冒頭のモデルreg100103aについて自力でVIFを求めるには下記の様にする。ただしこの方法は,特に独立変数の数が多い場合には手間がかかる。
Full <- complete.cases(data01$income, data01$age, data01$male, data01$edu)
y <- data01$income[Full]
x1 <- data01$age[Full]
x2 <- data01$male[Full]
x3 <- data01$edu[Full]
summary(lm(x1 ~ x2 + x3))
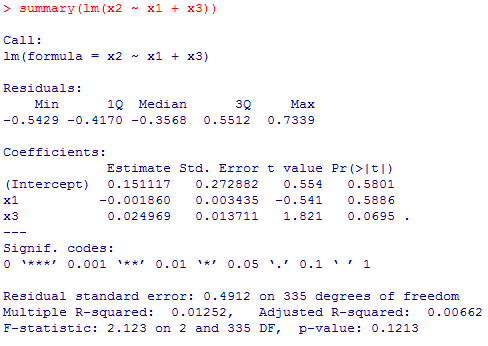
summary(lm(x2 ~ x1 + x3))
summary(lm(x3 ~ x1 + x2))
# vif
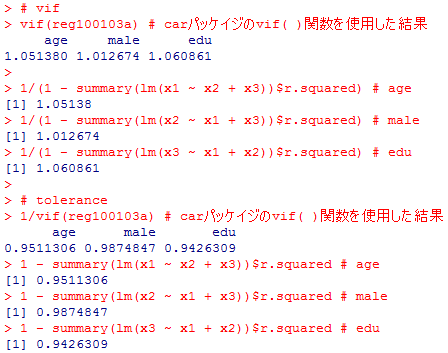
vif(reg100103a) # carパッケイジのvif( )関数を使用した結果
1/(1 - summary(lm(x1 ~ x2 + x3))$r.squared) # age
1/(1 - summary(lm(x2 ~ x1 + x3))$r.squared) # male
1/(1 - summary(lm(x3 ~ x1 + x2))$r.squared) # edu
# tolerance
1/vif(reg100103a) # carパッケイジのvif( )関数を使用した結果
1 - summary(lm(x1 ~ x2 + x3))$r.squared # age
1 - summary(lm(x2 ~ x1 + x3))$r.squared # male
1 - summary(lm(x3 ~ x1 + x2))$r.squared # edu
y <- data01$income[Full]
x1 <- data01$age[Full]
x2 <- data01$male[Full]
x3 <- data01$edu[Full]
summary(lm(x1 ~ x2 + x3))
summary(lm(x2 ~ x1 + x3))
summary(lm(x3 ~ x1 + x2))
# vif
vif(reg100103a) # carパッケイジのvif( )関数を使用した結果
1/(1 - summary(lm(x1 ~ x2 + x3))$r.squared) # age
1/(1 - summary(lm(x2 ~ x1 + x3))$r.squared) # male
1/(1 - summary(lm(x3 ~ x1 + x2))$r.squared) # edu
# tolerance
1/vif(reg100103a) # carパッケイジのvif( )関数を使用した結果
1 - summary(lm(x1 ~ x2 + x3))$r.squared # age
1 - summary(lm(x2 ~ x1 + x3))$r.squared # male
1 - summary(lm(x3 ~ x1 + x2))$r.squared # edu




1-4 変数のコントロールとは
本文で例示している予測値を求める。既に何度か紹介した方法である。

各カテゴリの実際の標本平均は次の様にして求める事が出来る。
summary(reg100103a)
coef100103a <- summary(reg100103a)$coefficients; coef100103a
sum(coef100103a[, 1]*c(1, 40, 0, 14))
sum(coef100103a[, 1]*c(1, 40, 0, 16))
sum(coef100103a[, 1]*c(1, 40, 1, 16))
coef100103a <- summary(reg100103a)$coefficients; coef100103a
sum(coef100103a[, 1]*c(1, 40, 0, 14))
sum(coef100103a[, 1]*c(1, 40, 0, 16))
sum(coef100103a[, 1]*c(1, 40, 1, 16))

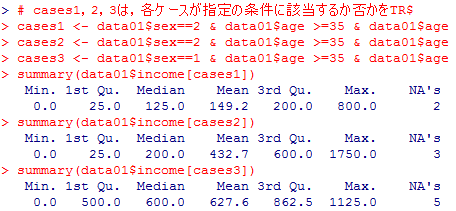
各カテゴリの実際の標本平均は次の様にして求める事が出来る。
# cases1,2,3は,各ケースが指定の条件に該当するか否かをTRUE(1)かFALSE(0)で表現するヴェクトル
cases1 <- data01$sex==2 & data01$age >=35 & data01$age <=44 & data01$edu==14
cases2 <- data01$sex==2 & data01$age >=35 & data01$age <=44 & data01$edu==16
cases3 <- data01$sex==1 & data01$age >=35 & data01$age <=44 & data01$edu==16
summary(data01$income[cases1])
summary(data01$income[cases2])
summary(data01$income[cases3])
cases1 <- data01$sex==2 & data01$age >=35 & data01$age <=44 & data01$edu==14
cases2 <- data01$sex==2 & data01$age >=35 & data01$age <=44 & data01$edu==16
cases3 <- data01$sex==1 & data01$age >=35 & data01$age <=44 & data01$edu==16
summary(data01$income[cases1])
summary(data01$income[cases2])
summary(data01$income[cases3])

発展1 一般線型モデル(GLM, LM)
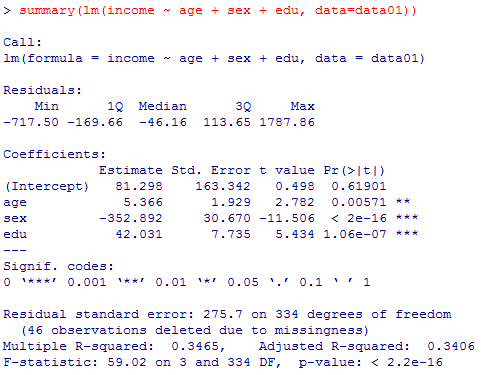
性別変数を3通りの方法で重回帰分析に投入したのが以下である。それぞれの結果をよく見比べて,何処が違うかを確認した上で,1番目と3番目についてはそれぞれ予測式を具体的に考えて,本質的に同じである事を確認しよう。
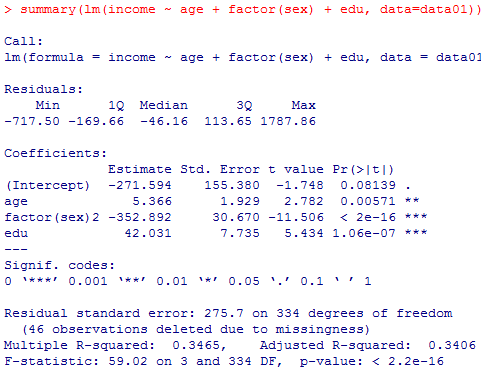
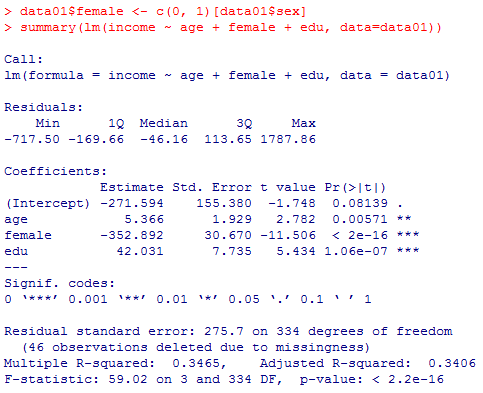
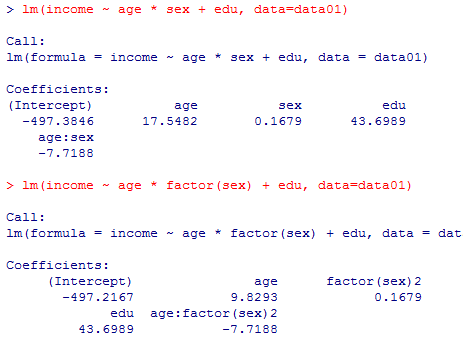
本文で言及している残りのモデルについても結果を掲示しておくので読み解いてみよう。(表示結果を簡略化する為にsummary( )ではなくlm( )の結果だけを示す。)
summary(lm(income ~ age + sex + edu, data=data01))
summary(lm(income ~ age + factor(sex) + edu, data=data01))
data01$female <- c(0, 1)[data01$sex]
summary(lm(income ~ age + female + edu, data=data01))
summary(lm(income ~ age + factor(sex) + edu, data=data01))
data01$female <- c(0, 1)[data01$sex]
summary(lm(income ~ age + female + edu, data=data01))



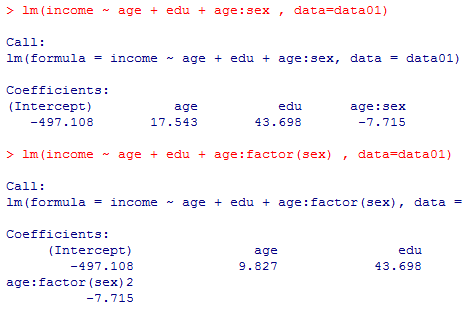
本文で言及している残りのモデルについても結果を掲示しておくので読み解いてみよう。(表示結果を簡略化する為にsummary( )ではなくlm( )の結果だけを示す。)
lm(income ~ age * sex + edu, data=data01)
lm(income ~ age * factor(sex) + edu, data=data01)
lm(income ~ age + edu + age:sex , data=data01)
lm(income ~ age + edu + age:factor(sex) , data=data01)
lm(income ~ age * factor(sex) + edu, data=data01)
lm(income ~ age + edu + age:sex , data=data01)
lm(income ~ age + edu + age:factor(sex) , data=data01)


発展2-1 変数選択
まずは本文と同様の変数減少法の結果を紹介した後,それ以外の変数選択法についても簡単に紹介する。
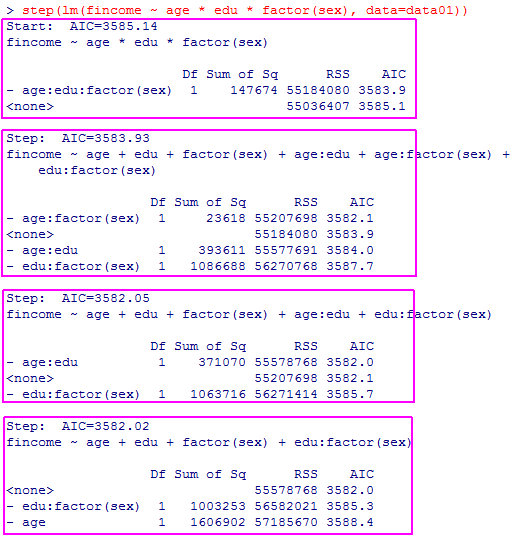
出力そのままではstepごとの区切りが分かりにくいかも知れないので,各ステップをピンクの枠線で囲んである。が何もしない場合であり,どれかの独立変数を除去したらAICが低下するかどうかを確かめながら,それ以上除去する独立変数がなくなった時点で終了する。最後に,採用されたモデルの偏回帰係数が出力される。
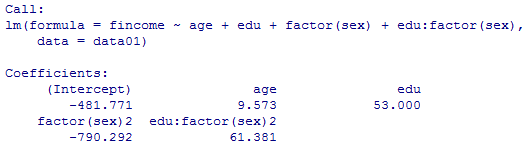
これをst1というオブジェクトに格納してsummary( )を見ると以下の通りである。また,各ステップの要点だけを表形式に表現するには,オブジェクトの中のanova情報を表示させる。オブジェクトst1に格納する際に上記と同じ変数選択の過程が出力されるが以下では省略する。

st1$anovaの結果は,1が出発点のモデル,そこから2,3,4と,AICが低下する限り変数を減少させていっている。

step( )関数で使用されているのはextractAIC( )の計算法と同じである事が分かる。AICはモデル同士のAICの差だけが重要で,それについてはextraxtAIC( )で計算してもAIC( )で計算しても同じであるので気にしなくて良い。

変数減少法の選択の最初に与えたモデルについても,AIC( )とextractAIC( )の結果の再現を示しておく。


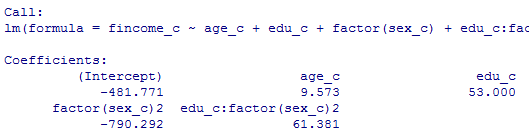

かなり長くなってしまったので,自分でよく見比べて異同を確認して欲しい。変数増加法では,出発点のモデルを変えると,最終結果がbothやbackwardとは異なってしまう事もある。object=lm(fincome_c ~ 1)などとして確認すると良い。
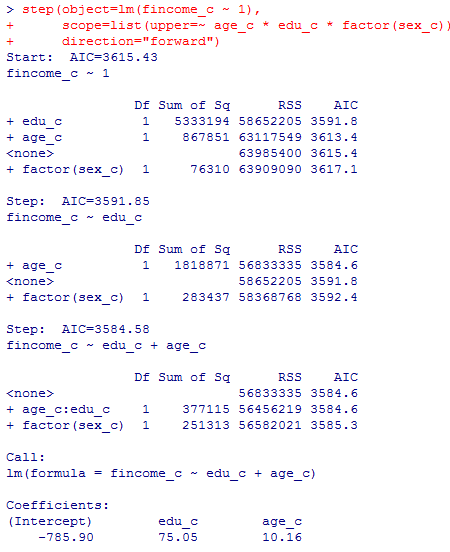
出力そのままではstepごとの区切りが分かりにくいかも知れないので,各ステップをピンクの枠線で囲んである。
step(lm(fincome ~ age * edu * factor(sex), data=data01))


これをst1というオブジェクトに格納してsummary( )を見ると以下の通りである。また,各ステップの要点だけを表形式に表現するには,オブジェクトの中のanova情報を表示させる。オブジェクトst1に格納する際に上記と同じ変数選択の過程が出力されるが以下では省略する。
st1 <- step(lm(fincome ~ age * edu * factor(sex), data=data01))
summary(st1) # 最終的に選択されたモデルの結果
names(st1) # オブジェクトに格納されている情報の名前一覧
st1$anova # 変数選択の過程で検討されたモデルの分散分析表
summary(st1) # 最終的に選択されたモデルの結果
names(st1) # オブジェクトに格納されている情報の名前一覧
st1$anova # 変数選択の過程で検討されたモデルの分散分析表

st1$anovaの結果は,1が出発点のモデル,そこから2,3,4と,AICが低下する限り変数を減少させていっている。
AIC(st1) # ある(単純な)計算方法におけるAIC
logLik(st1) # 対数尤度,dfとして最尤推定されるパラメタの個数kが示されている。独立変数の個数4個+2になっている。
(-2)*logLik(st1)+2*attributes(logLik(st1))$df # -2LL+2kを計算
extractAIC(st1) # 別の方法で計算されたAIC
logLik(st1) # 対数尤度,dfとして最尤推定されるパラメタの個数kが示されている。独立変数の個数4個+2になっている。
(-2)*logLik(st1)+2*attributes(logLik(st1))$df # -2LL+2kを計算
extractAIC(st1) # 別の方法で計算されたAIC

step( )関数で使用されているのはextractAIC( )の計算法と同じである事が分かる。AICはモデル同士のAICの差だけが重要で,それについてはextraxtAIC( )で計算してもAIC( )で計算しても同じであるので気にしなくて良い。
# extractAIC(st1)の結果を再現する
log(deviance(st1)/nrow(st1$model))*nrow(st1$model)+2*st1$rank
log(deviance(st1)/nrow(st1$model))*nrow(st1$model)+2*st1$rank

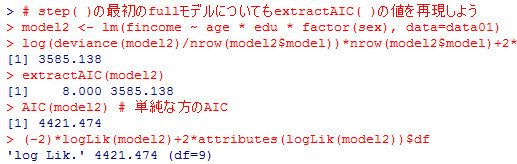
変数減少法の選択の最初に与えたモデルについても,AIC( )とextractAIC( )の結果の再現を示しておく。
# step( )の最初のfullモデルについてもextractAIC( )の値を再現しよう
model2 <- lm(fincome ~ age * edu * factor(sex), data=data01)
log(deviance(model2)/nrow(model2$model))*nrow(model2$model)+2*model2$rank
extractAIC(model2)
AIC(model2) # 単純な方のAIC
(-2)*logLik(model2)+2*attributes(logLik(model2))$df
model2 <- lm(fincome ~ age * edu * factor(sex), data=data01)
log(deviance(model2)/nrow(model2$model))*nrow(model2$model)+2*model2$rank
extractAIC(model2)
AIC(model2) # 単純な方のAIC
(-2)*logLik(model2)+2*attributes(logLik(model2))$df

いろいろな変数選択法
さて,漸く,よりカスタマイズした変数選択法の紹介である。
# 変数増加法において,モデルが複雑になるにつれて有効ケースが減少してしまうので,
# 最初から完備ケース分析の準備をしておく必要がある。
full <- complete.cases(data01$fincome, data01$age, data01$edu, data01$sex)
fincome_c <- data01$fincome[full]
age_c <- data01$age[full]
edu_c <- data01$edu[full]
sex_c <- data01$sex[full]
# 完備ケース分析用の変数はデータフレイムに格納していない点に注意
# 年齢+教育年数+性別の主効果だけからなるモデルを出発点(object)として,
# それらの二次の交互作用,三次の交互作用まで含むモデルを最大とする(scope)場合の
# 変数増加法(forward)。つまり,交互作用のどれを入れると良いかを検討している
step(object=lm(fincome_c ~ age_c + edu_c + factor(sex_c)),
scope=list(upper=~ age_c * edu_c * factor(sex_c)),
direction="forward")
# 変数増減法
step(lm(fincome_c ~ age_c * edu_c * factor(sex_c)), direction="both")
# 変数減少法
step(lm(fincome_c ~ age_c * edu_c * factor(sex_c)), direction="backward")
# 最初から完備ケース分析の準備をしておく必要がある。
full <- complete.cases(data01$fincome, data01$age, data01$edu, data01$sex)
fincome_c <- data01$fincome[full]
age_c <- data01$age[full]
edu_c <- data01$edu[full]
sex_c <- data01$sex[full]
# 完備ケース分析用の変数はデータフレイムに格納していない点に注意
# 年齢+教育年数+性別の主効果だけからなるモデルを出発点(object)として,
# それらの二次の交互作用,三次の交互作用まで含むモデルを最大とする(scope)場合の
# 変数増加法(forward)。つまり,交互作用のどれを入れると良いかを検討している
step(object=lm(fincome_c ~ age_c + edu_c + factor(sex_c)),
scope=list(upper=~ age_c * edu_c * factor(sex_c)),
direction="forward")
# 変数増減法
step(lm(fincome_c ~ age_c * edu_c * factor(sex_c)), direction="both")
# 変数減少法
step(lm(fincome_c ~ age_c * edu_c * factor(sex_c)), direction="backward")





かなり長くなってしまったので,自分でよく見比べて異同を確認して欲しい。変数増加法では,出発点のモデルを変えると,最終結果がbothやbackwardとは異なってしまう事もある。object=lm(fincome_c ~ 1)などとして確認すると良い。

発展2-2 誤差減少率(PRE)
前項2-2のst1と同等のモデル(完備ケース分析の処理済みのもの)について,分散説明率と誤差減少率が一致する事を(数式から自明ではあるが)一応確認しておく。

# st1と同じモデル。但し完備ケース分析の処理をしたもの。
reg100203 <- lm(fincome_c ~ age_c + edu_c + factor(sex_c) + edu_c*factor(sex_c))
summary(reg100203) # Multiple R-squaredを確認
SST <- var(fincome_c)*(length(fincome_c)-1); SST # 従属変数の偏差平方和
SSr <- var(reg100203$residuals)*(length(reg100203$residuals)-1); SSr # 残差平方和
# 誤差減少率の定義式に代入
1-SSr/SST # 平方和から計算
1-var(reg100203$residuals)/var(fincome_c) # (不偏)分散から計算
reg100203 <- lm(fincome_c ~ age_c + edu_c + factor(sex_c) + edu_c*factor(sex_c))
summary(reg100203) # Multiple R-squaredを確認
SST <- var(fincome_c)*(length(fincome_c)-1); SST # 従属変数の偏差平方和
SSr <- var(reg100203$residuals)*(length(reg100203$residuals)-1); SSr # 残差平方和
# 誤差減少率の定義式に代入
1-SSr/SST # 平方和から計算
1-var(reg100203$residuals)/var(fincome_c) # (不偏)分散から計算

第10章の【練習問題】の解答
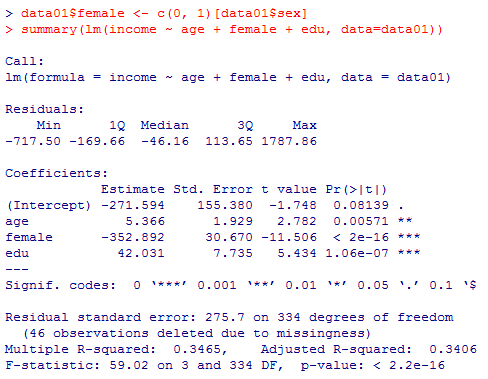
1) の答え: 以下の通りで,vifは非常に大きいが,ageとage^2はいずれも5%有意である。
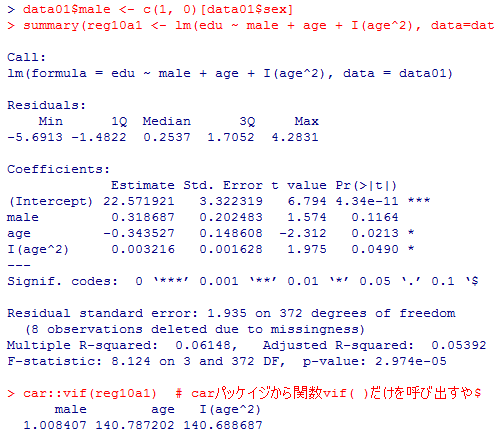
age^2の係数が正なので,年齢と教育年数の関係は下に凸な放物線となる。その頂点のx座標(年齢)は,以下の計算から約53.4歳となる。データに含まれるのは30歳〜59歳であるが,53歳以下の対象者では,若いほど教育年数が長い傾向があるが,50代半ば以降では(何故か)年長者の方が教育年数が長いという関係になる(50代後半では高学歴層の回答率が高かった可能性も考えられる)。
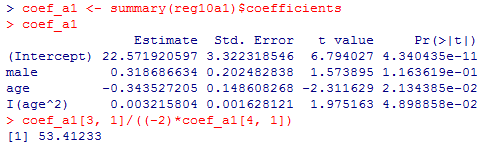
2) の答え: まず問題文の前半の結果は以下の通りである。vifの結果はどれもかなり悪いが,検定は5%水準〜10%水準で有意になっている。
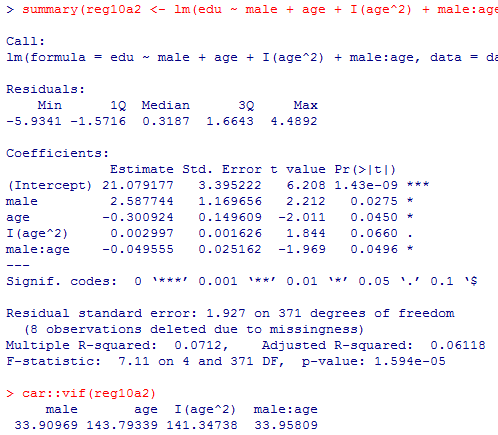
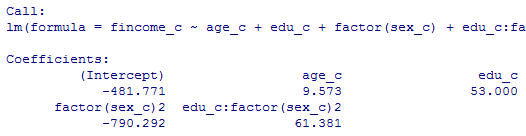
問題の後半である。表示の仕方に少し工夫をしたものも付加してある。自分で調べて解読すると良い。

3) の答え: まずは分析結果を確認し,予測式を男女別に数式表現する。
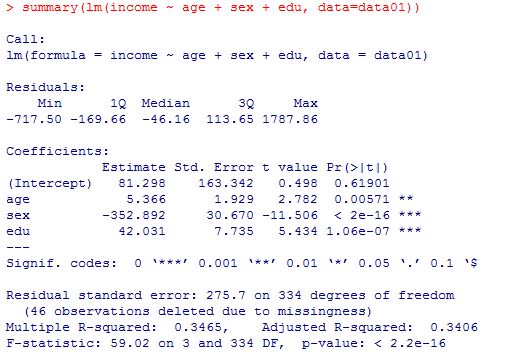
予測式は,income = 81.3 + 5.4*age - 353*sex + 42*edu となる。
ここで,age年齢は調査時満年齢,eduは教育年数であるが,sexは男性=1,女性=2という値である事に注意する。男性と女性でそれぞれ予測式を書き分けると以下の様になる。
男性の予測式:income = 81.3 + 5.4*age - 353*1 + 42*edu = income = -272 + 5.4*age + 42*edu
女性の予測式:income = 81.3 + 5.4*age - 353*2 + 42*edu = -625 + 5.4*age + 42*edu
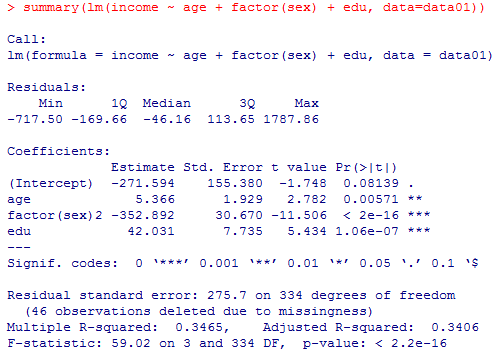
factor(sex)2というのは,factor(sex)が2の値を取る場合に,という意味であり,factor(sex)が1の値(男性)の場合は関係しない。
予測式は,income = -272 + 5.4*age - 353*factor(sex)2 + 42*edu となる。
factor(sex)2の項の意味に注意して予測式を書き分ける。
男性の予測式:income = -272 + 5.4*age + 42*edu
女性の予測式:income = -272 + 5.4*age - 353 + 42*edu = -625 + 5.4*age + 42*edu
となり,上の結果と一致する。factor(sex)を投入するのは,女性ダミー変数を投入するのと全く同じ事になる。
data01$male <- c(1, 0)[data01$sex]
summary(reg10a1 <- lm(edu ~ male + age + I(age^2), data=data01))
car::vif(reg10a1) # carパッケイジから関数vif( )だけを呼び出すやり方
summary(reg10a1 <- lm(edu ~ male + age + I(age^2), data=data01))
car::vif(reg10a1) # carパッケイジから関数vif( )だけを呼び出すやり方

age^2の係数が正なので,年齢と教育年数の関係は下に凸な放物線となる。その頂点のx座標(年齢)は,以下の計算から約53.4歳となる。データに含まれるのは30歳〜59歳であるが,53歳以下の対象者では,若いほど教育年数が長い傾向があるが,50代半ば以降では(何故か)年長者の方が教育年数が長いという関係になる(50代後半では高学歴層の回答率が高かった可能性も考えられる)。
coef_a1 <- summary(reg10a1)$coefficients
coef_a1
coef_a1[3, 1]/((-2)*coef_a1[4, 1])
coef_a1
coef_a1[3, 1]/((-2)*coef_a1[4, 1])

2) の答え: まず問題文の前半の結果は以下の通りである。vifの結果はどれもかなり悪いが,検定は5%水準〜10%水準で有意になっている。
summary(reg10a2 <- lm(edu ~ male + age + I(age^2) + male:age, data=data01))
car::vif(reg10a2)
car::vif(reg10a2)

問題の後半である。表示の仕方に少し工夫をしたものも付加してある。自分で調べて解読すると良い。
names(reg10a2)
coef10a2 <- reg10a2$coefficients # 定数項と偏回帰係数の行列を取り出す
p.age <- 50 # 予測式で求める年齢を,調査対象の30〜59歳から自由に指定。
p.male <- 1 # 男性なら1,女性なら0とする
profile <- c(1, p.male, p.age, p.age^2, p.male*p.age) # 独立変数行列
p.male; p.age
sum(coef10a2*profile)
# 一目でわかる出力を工夫してみる
sprintf("%s,%d歳の教育年数の予測値%.1f年", c("女性", "男性")[p.male+1], p.age, sum(coef10a2*profile))
coef10a2 <- reg10a2$coefficients # 定数項と偏回帰係数の行列を取り出す
p.age <- 50 # 予測式で求める年齢を,調査対象の30〜59歳から自由に指定。
p.male <- 1 # 男性なら1,女性なら0とする
profile <- c(1, p.male, p.age, p.age^2, p.male*p.age) # 独立変数行列
p.male; p.age
sum(coef10a2*profile)
# 一目でわかる出力を工夫してみる
sprintf("%s,%d歳の教育年数の予測値%.1f年", c("女性", "男性")[p.male+1], p.age, sum(coef10a2*profile))

3) の答え: まずは分析結果を確認し,予測式を男女別に数式表現する。
summary(lm(income ~ age + sex + edu, data=data01))
summary(lm(income ~ age + factor(sex) + edu, data=data01))
summary(lm(income ~ age + factor(sex) + edu, data=data01))

予測式は,income = 81.3 + 5.4*age - 353*sex + 42*edu となる。
ここで,age年齢は調査時満年齢,eduは教育年数であるが,sexは男性=1,女性=2という値である事に注意する。男性と女性でそれぞれ予測式を書き分けると以下の様になる。
男性の予測式:income = 81.3 + 5.4*age - 353*1 + 42*edu = income = -272 + 5.4*age + 42*edu
女性の予測式:income = 81.3 + 5.4*age - 353*2 + 42*edu = -625 + 5.4*age + 42*edu

factor(sex)2というのは,factor(sex)が2の値を取る場合に,という意味であり,factor(sex)が1の値(男性)の場合は関係しない。
予測式は,income = -272 + 5.4*age - 353*factor(sex)2 + 42*edu となる。
factor(sex)2の項の意味に注意して予測式を書き分ける。
男性の予測式:income = -272 + 5.4*age + 42*edu
女性の予測式:income = -272 + 5.4*age - 353 + 42*edu = -625 + 5.4*age + 42*edu
となり,上の結果と一致する。factor(sex)を投入するのは,女性ダミー変数を投入するのと全く同じ事になる。

Copyright (C) 2016-2017 SUGINO Isamu All Rights Reserved. design by tempnate

