杉野 勇 (SUGINO Isamu) お茶の水女子大学・人間発達科学専攻・応用社会学コース担当
『入門・社会統計学』サポートウェブ |
|
第11章 主成分分析(PCA)と（探索的）因子分析(EFA)
1-1 データが有する情報量の次元の縮約
ここでも引き続きデータフレイム名はdata01としておく。まずは使用する変数の度数分布から，欠損値処理が必要かどうかを確認し，必要なものは処理をする。
# 欠損値の指定
table(data01$q0101, useNA="always")
table(data01$q0102, useNA="always")
table(data01$q0103, useNA="always")
table(data01$q0200, useNA="always")
table(data01$q0301, useNA="always")
table(data01$q0302, useNA="always")
table(data01$q0401, useNA="always")
table(data01$q0402, useNA="always")
table(data01$q0403, useNA="always")
data01$q0103[data01$q0103 ==9] <- NA
data01$q0200[data01$q0200 ==7] <- NA
次に，使用する変数だけ取り出してオブジェクトvarsに纏めておき，そこから完備ケース分析用にケース選択したvarsを作成する。table(data01$q0101, useNA="always")
table(data01$q0102, useNA="always")
table(data01$q0103, useNA="always")
table(data01$q0200, useNA="always")
table(data01$q0301, useNA="always")
table(data01$q0302, useNA="always")
table(data01$q0401, useNA="always")
table(data01$q0402, useNA="always")
table(data01$q0403, useNA="always")
data01$q0103[data01$q0103 ==9] <- NA
data01$q0200[data01$q0200 ==7] <- NA
# ここでは，使用する変数だけを取り出してまとめておく
vars0 <- cbind(data01$q0101, data01$q0102, data01$q0103,
data01$q0200, data01$q0301, data01$q0302,
data01$q0401, data01$q0402, data01$q0403)
vars <- vars0[complete.cases(vars0),] # 完備ケース分析の準備
こうすれば主成分分析は簡単に出来る。vars0 <- cbind(data01$q0101, data01$q0102, data01$q0103,
data01$q0200, data01$q0301, data01$q0302,
data01$q0401, data01$q0402, data01$q0403)
vars <- vars0[complete.cases(vars0),] # 完備ケース分析の準備
(pr1 <- prcomp(vars, scale=T)) # 主成分分析を実行して結果を表示
scale=Tというオプションは元の変数を標準化するというオプションである。標準化の関数がscale( )であったことを思い出そう。prcomp( )関数のデフォルトはscale=Fであり，明示的に指定しないと標準化されない。標準化をしないと元の変数の単位や散布度の違いによって結果が影響される。元の変数の散布度の違いも重要であるならばそれでも良いが，ここでの分析例のようにそもそも単位がまったく違ったり散布度の違いが重要でない場合は，明示的にscale=Tとすることが必要である。scale=Fが分散共分散行列の固有値分解に，scale=Tが相関係数行列の固有値分解に対応する。
names(pr1) # 主成分分析の結果に含まれる情報名を確認
pr1$sdev^2 # 標準偏差を二乗して分散（＝固有値）を求める。
eigen(cor(vars)) # 相関係数行列を固有値分解すると，主成分分析の結果と一致する。
pr1$sdev^2 # 標準偏差を二乗して分散（＝固有値）を求める。
eigen(cor(vars)) # 相関係数行列を固有値分解すると，主成分分析の結果と一致する。
1-2 主成分の選出
主成分分析の結果pr1のsummary( )と，固有値のグラフ化を行う。本文よりも少しオプションを付けておこう。
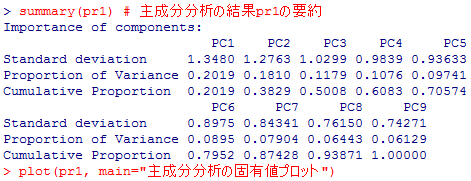
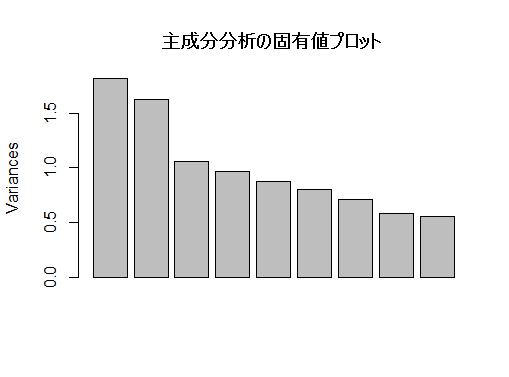
以下の様にオプションを付けると，よくある固有値プロットの様に折れ線グラフになる。
summary(pr1) # 主成分分析の結果pr1の要約
plot(pr1, main="主成分分析の固有値プロット")
plot(pr1, main="主成分分析の固有値プロット")
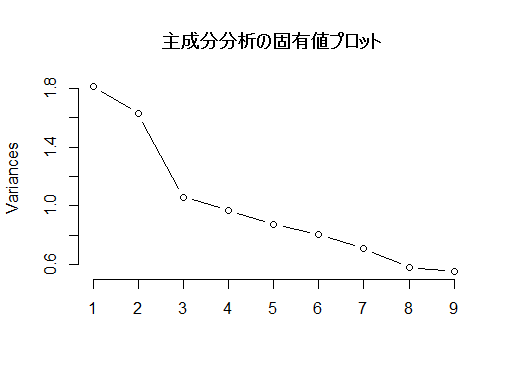
以下の様にオプションを付けると，よくある固有値プロットの様に折れ線グラフになる。
plot(pr1, main="主成分分析の固有値プロット", type="l")
1-3 主成分と元の変数の関係の解釈
主成分分析の結果をオブジェクトpr1に格納してあるが，主成分得点はpr1$xで取り出せる。主成分得点は最大の9つまで算出されており，それが有効ケース数だけある。pr1$xをすべて表示させると長大になるので，head( )関数を使って最初の6ケース分だけ表示してみる。
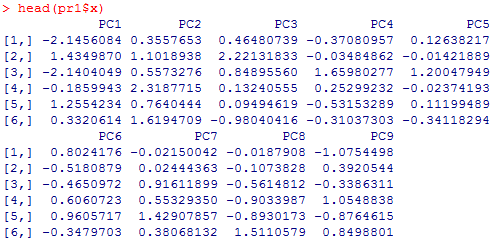
主成分ヴェクトルpr1$rotationも表示させてみよう。
第1主成分得点はpr1$x[,1]で取り出せるが，元のデータ行列を標準化したものscale(vars)と第1主成分ヴェクトルpr1$rotation[,1]から主成分得点を手動で合成することもできる。以下のようにするとその二つを並べて比較し，完全に一致していることが確認できる。%*%は行列の積の演算子である。
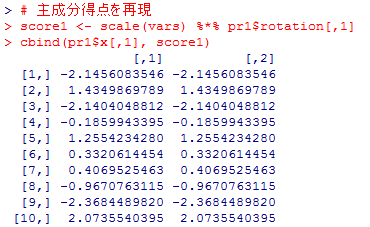
主成分負荷量（主成分得点と元の変数との積率相関係数）は以下の通り。行が元の9項目の観測変数である。
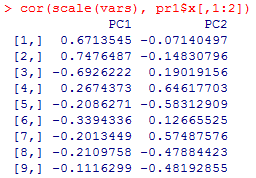
主成分負荷量は，主成分分析の結果の情報から以下の様にも求められる。t( )は転置行列を与える関数である。上の結果と一致してる事を確認しよう。
各ケースの位置関係と，元々の各変数の位置関係を同時に図示するのが，biplot( )関数である。第1主成分と第2主成分の関係を図示するには，biplot(pr1)だけでよい。
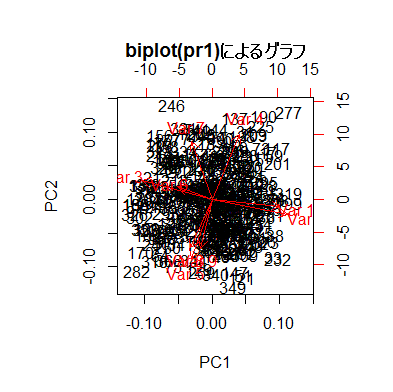
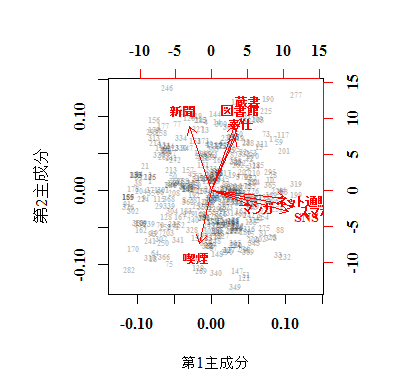
SNS書き込みや図書館，マンガやヴォランティアなどの変数の値を反転させて分かりやすくした変数行列vars1を主成分分析し，いくつかのグラフオプションを指定して描いてみる。各変数は主成分ヴェクトルの定数倍（定数はケース数の平方根×標準偏差）でプロットされ（上目盛りと右目盛り），各ケースは主成分得点の定数倍（ケース数の平方根×標準偏差の逆数）でプロットされている（下目盛りと左目盛り）。ケース数が多いとケースのプロットはあまり役に立たないかも知れない。また，目盛りの値自体は気にせず，変数相互の位置関係を読み取るとよい。
主成分ヴェクトルpr1$rotationも表示させてみよう。
第1主成分得点はpr1$x[,1]で取り出せるが，元のデータ行列を標準化したものscale(vars)と第1主成分ヴェクトルpr1$rotation[,1]から主成分得点を手動で合成することもできる。以下のようにするとその二つを並べて比較し，完全に一致していることが確認できる。%*%は行列の積の演算子である。
# 主成分得点を再現
score1 <- scale(vars) %*% pr1$rotation[,1]
cbind(pr1$x[,1], score1)
score1 <- scale(vars) %*% pr1$rotation[,1]
cbind(pr1$x[,1], score1)
主成分負荷量（主成分得点と元の変数との積率相関係数）は以下の通り。行が元の9項目の観測変数である。
主成分負荷量は，主成分分析の結果の情報から以下の様にも求められる。t( )は転置行列を与える関数である。上の結果と一致してる事を確認しよう。
t(pr1$rotation) * pr1$sdev
(t(pr1$rotation) * pr1$sdev)[1:2,]
t((t(pr1$rotation) * pr1$sdev)[1:2,])
(t(pr1$rotation) * pr1$sdev)[1:2,]
t((t(pr1$rotation) * pr1$sdev)[1:2,])
各ケースの位置関係と，元々の各変数の位置関係を同時に図示するのが，biplot( )関数である。第1主成分と第2主成分の関係を図示するには，biplot(pr1)だけでよい。
SNS書き込みや図書館，マンガやヴォランティアなどの変数の値を反転させて分かりやすくした変数行列vars1を主成分分析し，いくつかのグラフオプションを指定して描いてみる。各変数は主成分ヴェクトルの定数倍（定数はケース数の平方根×標準偏差）でプロットされ（上目盛りと右目盛り），各ケースは主成分得点の定数倍（ケース数の平方根×標準偏差の逆数）でプロットされている（下目盛りと左目盛り）。ケース数が多いとケースのプロットはあまり役に立たないかも知れない。また，目盛りの値自体は気にせず，変数相互の位置関係を読み取るとよい。
## 反転項目の調整
data01$q0103r <- max(data01$q0103, na.rm=T)-data01$q0103+1
data01$q0301r <- max(data01$q0301, na.rm=T)-data01$q0301+1
data01$q0302r <- max(data01$q0302, na.rm=T)-data01$q0302+1
data01$q0402r <- max(data01$q0402, na.rm=T)-data01$q0402+1
# 必要な変数だけを取り出す
vars1e <- cbind(data01$q0101, data01$q0102, data01$q0103r,
data01$q0200, data01$q0301r, data01$q0302r,
data01$q0401, data01$q0402r, data01$q0403)
# 完備ケース分析
vars1 <- vars1e[complete.cases(vars1e),]
# 主成分分析の実行と結果表示
(pr2 <- prcomp(vars1, scale=T))
# 主成分負荷量の計算
cor(scale(vars1), pr2$x)[,1:2]
# 作図の準備と作図
dimnames(pr2$rotation)[[1]] <- c("ネット通販", "スマホ", "SNS",
"蔵書", "図書館", "マンガ", "新聞", "奉仕", "喫煙")
biplot(pr2, cex=c(0.5, 0.8), col=c("#00000040", "red"),
font=2, family="serif", xlab="第1主成分", ylab="第2主成分")
data01$q0103r <- max(data01$q0103, na.rm=T)-data01$q0103+1
data01$q0301r <- max(data01$q0301, na.rm=T)-data01$q0301+1
data01$q0302r <- max(data01$q0302, na.rm=T)-data01$q0302+1
data01$q0402r <- max(data01$q0402, na.rm=T)-data01$q0402+1
# 必要な変数だけを取り出す
vars1e <- cbind(data01$q0101, data01$q0102, data01$q0103r,
data01$q0200, data01$q0301r, data01$q0302r,
data01$q0401, data01$q0402r, data01$q0403)
# 完備ケース分析
vars1 <- vars1e[complete.cases(vars1e),]
# 主成分分析の実行と結果表示
(pr2 <- prcomp(vars1, scale=T))
# 主成分負荷量の計算
cor(scale(vars1), pr2$x)[,1:2]
# 作図の準備と作図
dimnames(pr2$rotation)[[1]] <- c("ネット通販", "スマホ", "SNS",
"蔵書", "図書館", "マンガ", "新聞", "奉仕", "喫煙")
biplot(pr2, cex=c(0.5, 0.8), col=c("#00000040", "red"),
font=2, family="serif", xlab="第1主成分", ylab="第2主成分")
2-1 潜在変数(latent variable)から観測変数(observed variable)への影響
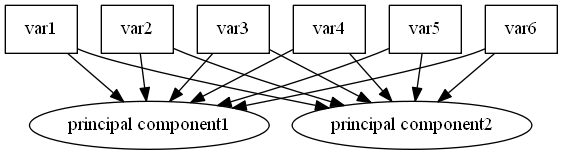
主成分分析と（探索的）因子分析の違いを，グラフで表現してみよう。調査で実際に回答などの形で情報（数値）を得られている観測変数を var1 などと表記し，□で表す。それに対して，主成分(principal component)や因子(factor)など，直接観測されていない潜在変数を○で表す。因子分析においてはその他に独自因子（＝誤差; error）を e1 などと表記し，○も□もつけない事とする。
主成分分析(PCA; Principal Component Analysis)のモデルを図示すると以下の様になる。観測された変数を元に，主成分得点を合成するのである。
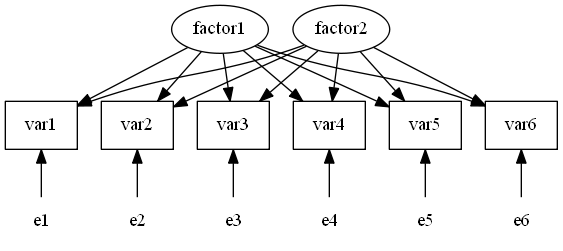
これに対し，（探索的）因子分析(EFA; Exploratory Factor Analysis)のモデルを図示すると以下の様になる。潜在変数と観測変数の間のパス＝矢印（規定関係）が主成分分析とは逆であるのに加え，観測変数にはそれ以外に誤差（独自因子）からのパスも引かれている。
因みにこれらのグラフはGraphviz; Graph Visualization Softwareを用いて作成した。コマンドはWatanabe Shin, 「Graphvizとdot言語でグラフを描く方法のまとめ」(2017年3月8日閲覧)を見ながら書くとこの程度のものは何とか書ける様になるだろう。結果の保存の仕方はやや分かりにくいので注意する事。使用したコマンド（dot言語）のファイルも提供しておく： 主成分分析グラフ，（探索的）因子分析グラフ
主成分分析(PCA; Principal Component Analysis)のモデルを図示すると以下の様になる。観測された変数を元に，主成分得点を合成するのである。
これに対し，（探索的）因子分析(EFA; Exploratory Factor Analysis)のモデルを図示すると以下の様になる。潜在変数と観測変数の間のパス＝矢印（規定関係）が主成分分析とは逆であるのに加え，観測変数にはそれ以外に誤差（独自因子）からのパスも引かれている。
因みにこれらのグラフはGraphviz; Graph Visualization Softwareを用いて作成した。コマンドはWatanabe Shin, 「Graphvizとdot言語でグラフを描く方法のまとめ」(2017年3月8日閲覧)を見ながら書くとこの程度のものは何とか書ける様になるだろう。結果の保存の仕方はやや分かりにくいので注意する事。使用したコマンド（dot言語）のファイルも提供しておく： 主成分分析グラフ，（探索的）因子分析グラフ
2-2 因子の選出
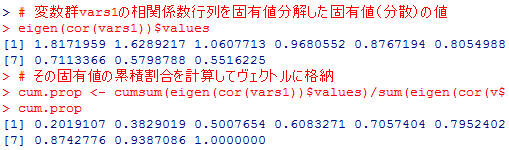
変数群vars1を固有値分解した結果の固有値のスクリープロットを，色々と装飾しながら描いてみる。赤が各因子の固有値の大きさ，青は累積割合である。
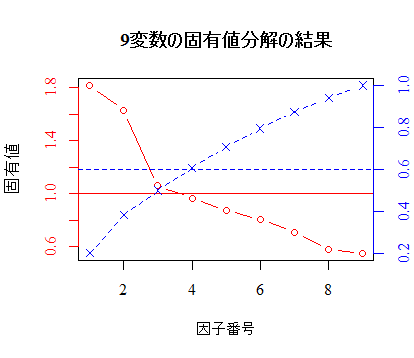
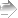清水裕士「因子分析における因子数選択のための基準」2012年5月23日），場合によっては何度か繰り返すうちに適切な因子数が1だけ変化する事が有り得る。この分析例では，3もしくは4の因子数が適切となった。
また，分析のたびにグラフを出力する。PCは主成分分析の場合，FAは因子分析の場合である。赤い点線で表されているシミュレイションの結果よりも固有値が大きければ採用すべきとなる。
# 変数群vars1の相関係数行列を固有値分解した固有値（分散）の値
eigen(cor(vars1))$values
# その固有値の累積割合を計算してヴェクトルに格納
cum.prop <- cumsum(eigen(cor(vars1))$values)/sum(eigen(cor(vars1))$values)
cum.prop
# 各固有値のグラフ
plot(eigen(cor(vars1))$values, type="b", family="serif", col="red",
xlab="因子番号", ylab="固有値", main="9変数の固有値分解の結果", yaxt="n")
axis(side=2, col="red", col.axis="red", family="serif")
abline(h=1, col="red") # 固有値1以上の基準線
par(new=T) # グラフの重ね描き
# 固有値の累積割合のグラフ
plot(cum.prop, type="b", col="blue", axes=F, xlab="", ylab="",
pch=4, lty=2)
axis(side=4, col="blue", col.axis="blue", family="serif")
abline(h=.6, col="blue", lty=2) # 累積割合60%の基準線
eigen(cor(vars1))$values
# その固有値の累積割合を計算してヴェクトルに格納
cum.prop <- cumsum(eigen(cor(vars1))$values)/sum(eigen(cor(vars1))$values)
cum.prop
# 各固有値のグラフ
plot(eigen(cor(vars1))$values, type="b", family="serif", col="red",
xlab="因子番号", ylab="固有値", main="9変数の固有値分解の結果", yaxt="n")
axis(side=2, col="red", col.axis="red", family="serif")
abline(h=1, col="red") # 固有値1以上の基準線
par(new=T) # グラフの重ね描き
# 固有値の累積割合のグラフ
plot(cum.prop, type="b", col="blue", axes=F, xlab="", ylab="",
pch=4, lty=2)
axis(side=4, col="blue", col.axis="blue", family="serif")
abline(h=.6, col="blue", lty=2) # 累積割合60%の基準線
パッケイジ"psych"のfa.parallel( )関数による平行分析
適切な因子数を決定する為に，やや専門的な「平行分析」を行ってみる。パッケイジpsychが必要になるので，インストールしていなければ，install.packages("psych", repos="http://cran.ism.ac.jp/") などとしてインストールする必要がある。既にインストールしてある場合には，library(psych)としてパッケイジを有効化するか，或いは以下の様にダブルコロンを用いてパッケイジの中の特定の関数だけを呼び出す。この分析は乱数を発生させて，乱数の相関係数行列を固有値分解した結果と比較する為（清水裕士「因子分析における因子数選択のための基準」2012年5月23日），場合によっては何度か繰り返すうちに適切な因子数が1だけ変化する事が有り得る。この分析例では，3もしくは4の因子数が適切となった。
psych::fa.parallel(vars1, SMC=TRUE)
また，分析のたびにグラフを出力する。PCは主成分分析の場合，FAは因子分析の場合である。赤い点線で表されているシミュレイションの結果よりも固有値が大きければ採用すべきとなる。
2-3 因子負荷量(factor loadings)と寄与率(contribution)
Rで因子分析を行う関数も複数あるが，まずは標準の因子分析の関数factanal( )で分析する。出力結果を見やすくする為に，先に変数群のヴェクトルvars1に列名（変数ラベル）を付けておく。
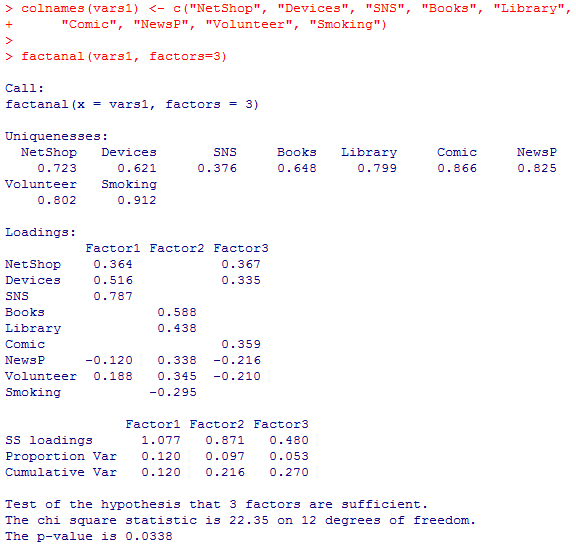
独自因子（言い換えれば誤差）Uniquenesses，因子負荷量Loadings（線型方程式の係数），因子寄与（寄与度）SS loadings（因子負荷量の二乗和），分散割合Proportion Var，累積分散割合Cumulative Var，因子数についての検定結果を確認しよう。
因子数の検定結果は，4因子の場合も当該箇所だけ紹介しよう。「4因子で十分である」とのゼロ仮説は5%水準で棄却されなかった。
…（中略）…
標準のfactanal( )関数では，斜交promax解の因子間相関係数行列が正しく出力されない問題について，詳しくは説明しないが，一致しなければいけない筈の結果が食い違ってしまう事だけ示しておこう。以下のサイトも参考になる。
緒賀郷志「Rによる因子分析関連メモ&主成分分析とその回転メモ」(2016年11月15日閲覧)
裏 RjpWiki「因子間相関係数行列がへん?」(2016年11月15日閲覧)
非回転解をヴァリマックス回転するには以下の様にする。
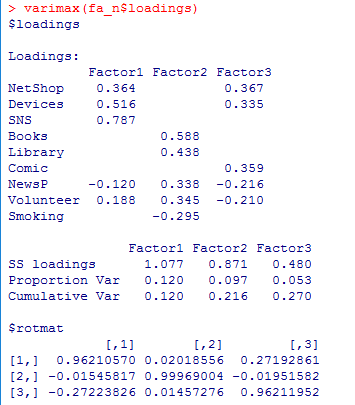
factanal( )関数の非回転解で計算させた因子得点（因子スコア）の要約統計量を求めるのは下記。
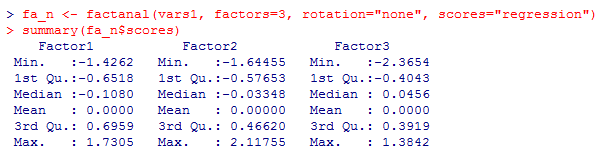
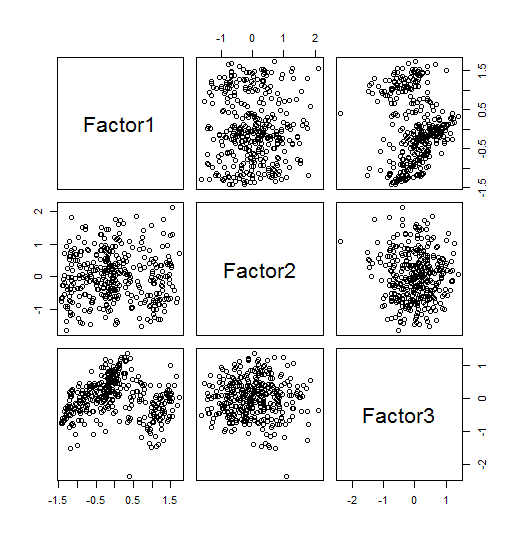
因子得点の散布図を行列形式で描画したければ次の様にすればよい。
独自因子（言い換えれば誤差）Uniquenesses，因子負荷量Loadings（線型方程式の係数），因子寄与（寄与度）SS loadings（因子負荷量の二乗和），分散割合Proportion Var，累積分散割合Cumulative Var，因子数についての検定結果を確認しよう。
因子数の検定結果は，4因子の場合も当該箇所だけ紹介しよう。「4因子で十分である」とのゼロ仮説は5%水準で棄却されなかった。
…（中略）…
標準のfactanal( )関数では，斜交promax解の因子間相関係数行列が正しく出力されない問題について，詳しくは説明しないが，一致しなければいけない筈の結果が食い違ってしまう事だけ示しておこう。以下のサイトも参考になる。
緒賀郷志「Rによる因子分析関連メモ&主成分分析とその回転メモ」(2016年11月15日閲覧)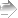裏 RjpWiki「因子間相関係数行列がへん?」(2016年11月15日閲覧)
factanal(vars1, factors=3, rotation="promax") # 標準でのpromax解
# 標準で（回転させない）初期解を求めてpromax( )関数に与える
fa_n <- factanal(vars1, factors=3, rotation="none"); promax(fa_n$loadings)
# 因子間相関行列を求める
solve(t(promax(fa_n$loadings)$rotmat) %*% promax(fa_n$loadings)$rotmat)
# psychパッケイジのfa( )関数を使用するので，インストールした事が無ければまずインストールする
# install.packages("psych", repos="https://cran.ism.ac.jp")
psych::fa(vars1, nfactors=3, rotate="promax", scores="regression", fm="ml")
fa_p2 <- psych::fa(vars1, nfactors=3, rotate="promax", scores="regression", fm="ml")
fa_p2$Phi
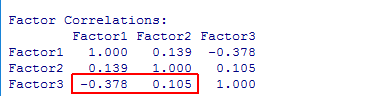
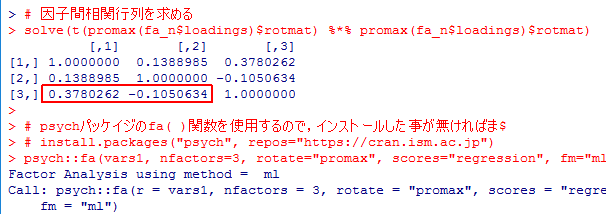
出力を全て掲載すると分かりにくいので，一部だけ抜粋して掲載する。赤い枠で囲った部分を比較する。3つある相関係数行列のうちの最初の1つだけが符号が誤っている。最後のものは因子の並び順が異なっている事に注意。# 標準で（回転させない）初期解を求めてpromax( )関数に与える
fa_n <- factanal(vars1, factors=3, rotation="none"); promax(fa_n$loadings)
# 因子間相関行列を求める
solve(t(promax(fa_n$loadings)$rotmat) %*% promax(fa_n$loadings)$rotmat)
# psychパッケイジのfa( )関数を使用するので，インストールした事が無ければまずインストールする
# install.packages("psych", repos="https://cran.ism.ac.jp")
psych::fa(vars1, nfactors=3, rotate="promax", scores="regression", fm="ml")
fa_p2 <- psych::fa(vars1, nfactors=3, rotate="promax", scores="regression", fm="ml")
fa_p2$Phi
非回転解をヴァリマックス回転するには以下の様にする。
factanal( )関数の非回転解で計算させた因子得点（因子スコア）の要約統計量を求めるのは下記。
因子得点の散布図を行列形式で描画したければ次の様にすればよい。
2-4 因子の解釈
本文同様にプロマックス解の結果を出力する。
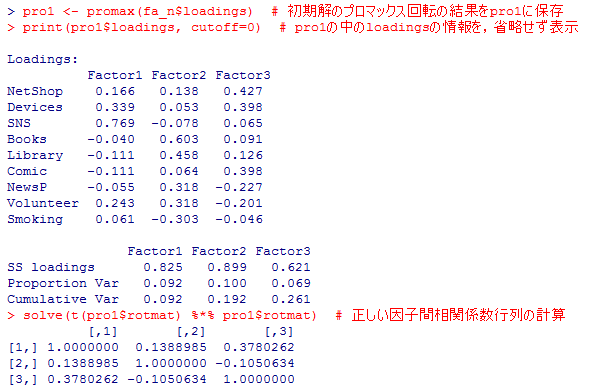
グラフを作図するには，以下の様に biplot( ) を使用する事も出来る。
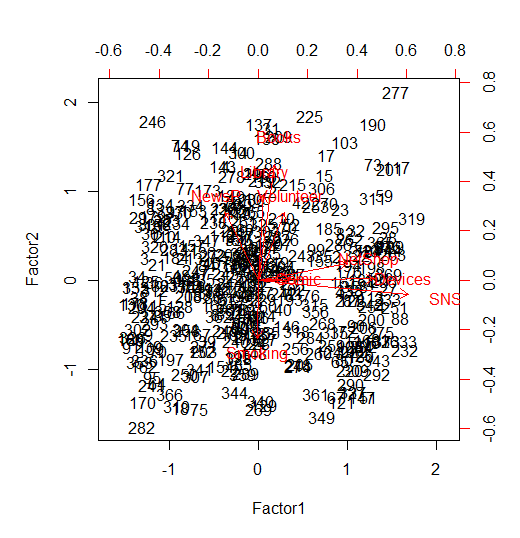
しかしこれではあまり分かり易くないので，次の様に手動で描いてみる。
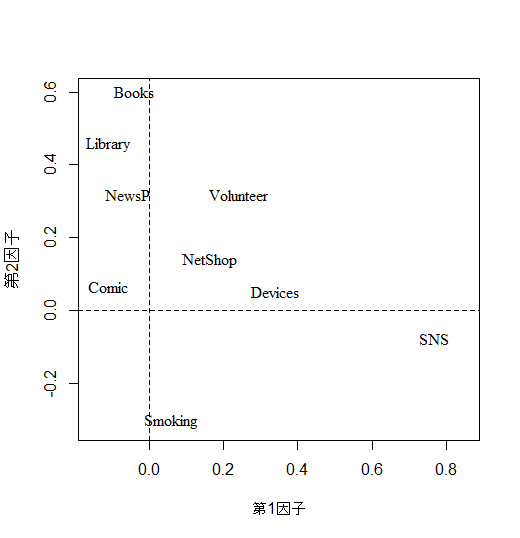
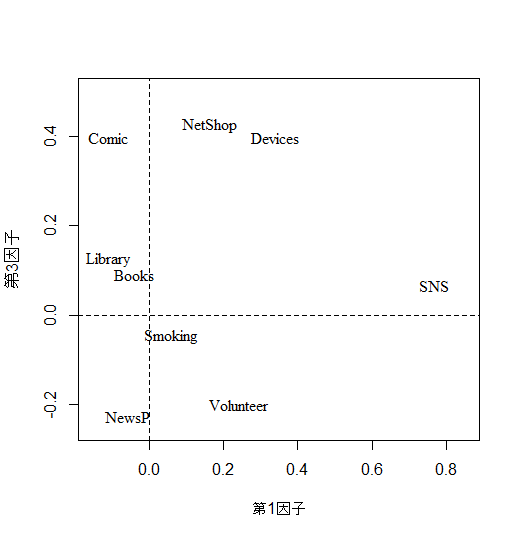
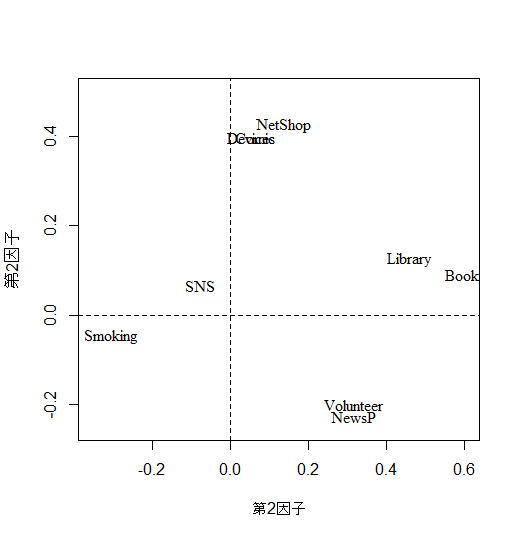
第1因子と第3因子，第2因子と第3因子の因子パタンのグラフも作成する。
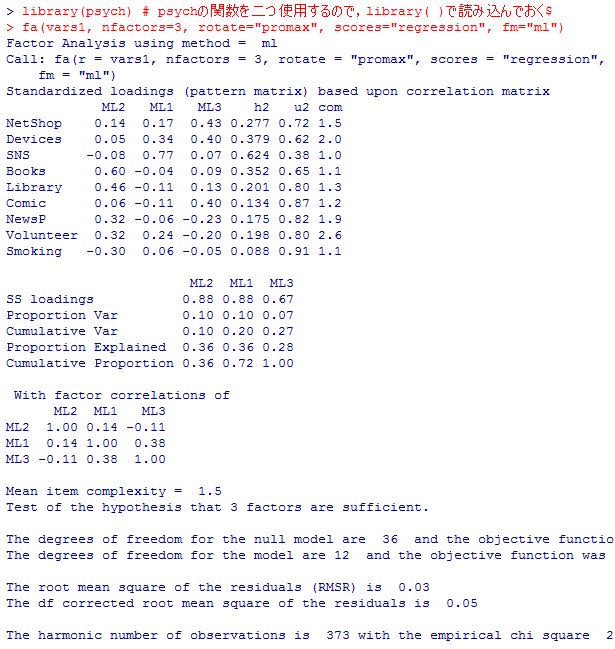
pro1 <- promax(fa_n$loadings) # 初期解のプロマックス回転の結果をpro1に保存
print(pro1$loadings, cutoff=0) # pro1の中のloadingsの情報を，省略せず表示
solve(t(pro1$rotmat) %*% pro1$rotmat) # 正しい因子間相関係数行列の計算
print(pro1$loadings, cutoff=0) # pro1の中のloadingsの情報を，省略せず表示
solve(t(pro1$rotmat) %*% pro1$rotmat) # 正しい因子間相関係数行列の計算
グラフを作図するには，以下の様に biplot( ) を使用する事も出来る。
biplot(fa_n$scores, fa_n$loadings)
しかしこれではあまり分かり易くないので，次の様に手動で描いてみる。
plot(NULL, xlim=c(-.15, .85), ylim=c(-.32, .6), xlab="第1因子", ylab="第2因子")
abline(h=0, v=0, lty=2) # 原点を通る座標を追加
text(pro1$loadings[,c(1,2)], colnames(vars1), family="serif")
abline(h=0, v=0, lty=2) # 原点を通る座標を追加
text(pro1$loadings[,c(1,2)], colnames(vars1), family="serif")
第1因子と第3因子，第2因子と第3因子の因子パタンのグラフも作成する。
plot(NULL, xlim=c(-.15, .85), ylim=c(-.25, .5), xlab="第1因子", ylab="第3因子")
abline(h=0, v=0, lty=2) # 原点を通る座標を追加
text(pro1$loadings[,c(1,3)], colnames(vars1), family="serif")
plot(NULL, xlim=c(-.35, .6), ylim=c(-.25, .5), xlab="第2因子", ylab="第2因子")
abline(h=0, v=0, lty=2) # 原点を通る座標を追加
text(pro1$loadings[,c(2,3)], colnames(vars1), family="serif")
abline(h=0, v=0, lty=2) # 原点を通る座標を追加
text(pro1$loadings[,c(1,3)], colnames(vars1), family="serif")
plot(NULL, xlim=c(-.35, .6), ylim=c(-.25, .5), xlab="第2因子", ylab="第2因子")
abline(h=0, v=0, lty=2) # 原点を通る座標を追加
text(pro1$loadings[,c(2,3)], colnames(vars1), family="serif")
パッケイジ"psych"のfa( )関数とalpha( )関数
psychパッケイジのfa( )関数と，クロンバックのα係数による内的整合性の検討の為のalpha( )関数の結果をフルサイズで掲載しておく。
library(psych) # psychの関数を二つ使用するので，library( )で読み込んでおく。
fa(vars1, nfactors=3, rotate="promax", scores="regression", fm="ml") alpha(vars1[,1:3])
fa(vars1, nfactors=3, rotate="promax", scores="regression", fm="ml") alpha(vars1[,1:3])
発展1-1 確証的因子分析(CFA)と構造方程式モデリング(SEM)
構造方程式モデリング(SEM; Structural Equation Modelling)によって確証的因子分析(CFA; Confirmatory Factor Analyis)を行ってみよう。あくまで説明用の初歩的なものであるが，本文では省略せざるを得なかったスクリプトや出力を全て掲示する。
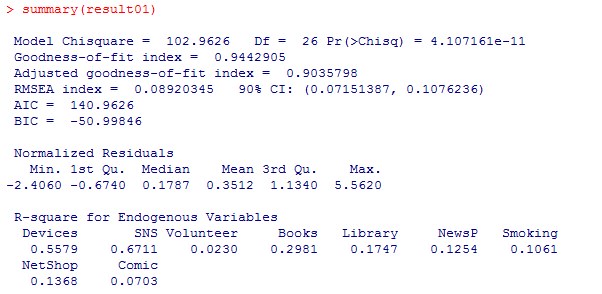
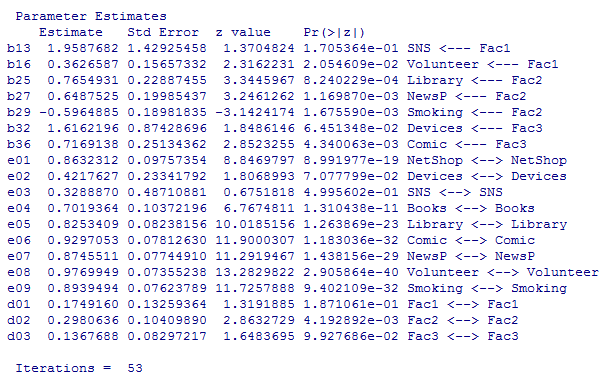
modIndices( )関数を使って，どうしたらモデルが改善するかの示唆を得よう。
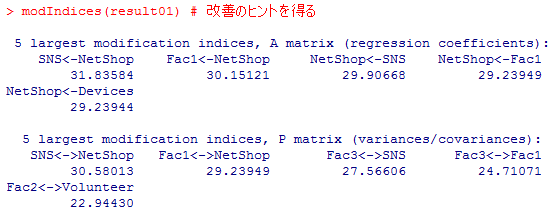
NetShop<-Fac1 から，第1因子からネットショッピングへのパスを追加し，Fac3<->Fac1 から，第1因子と第3因子に相関を追加すると良いと考えられる。
update( )関数を使ってmodel01を更新する。
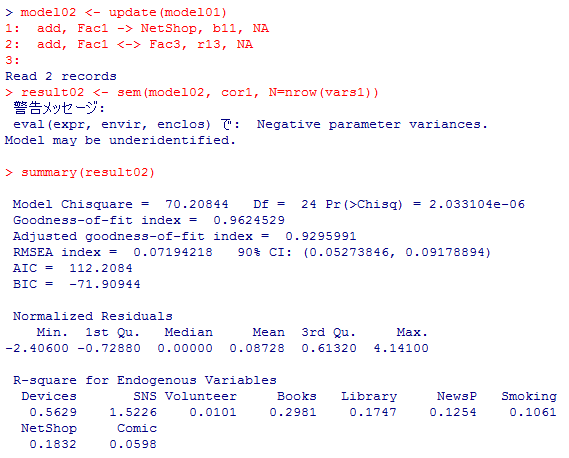
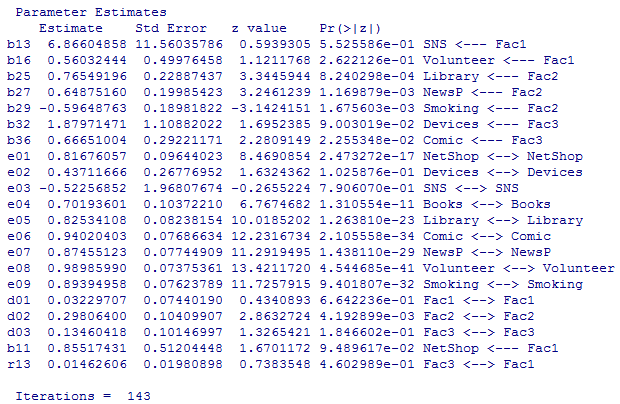
適合度指標は改善しているが，e03のSNSの分散がマイナスとなり，本来は不適切な解になっている。警告メッセージの「Negative parameter variances.」がそれを示している。
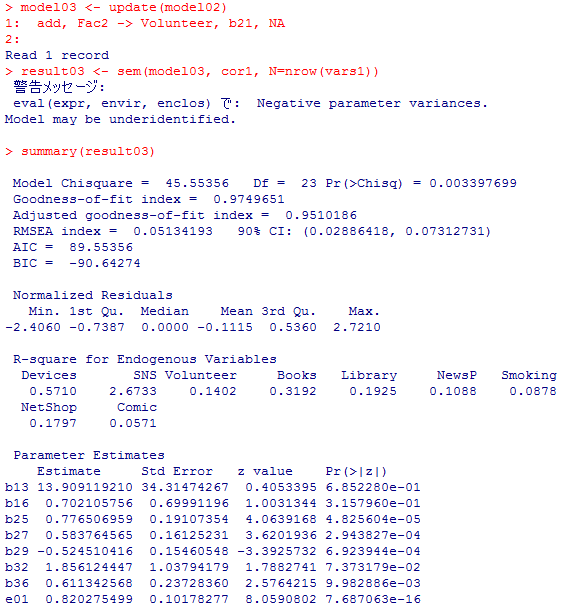
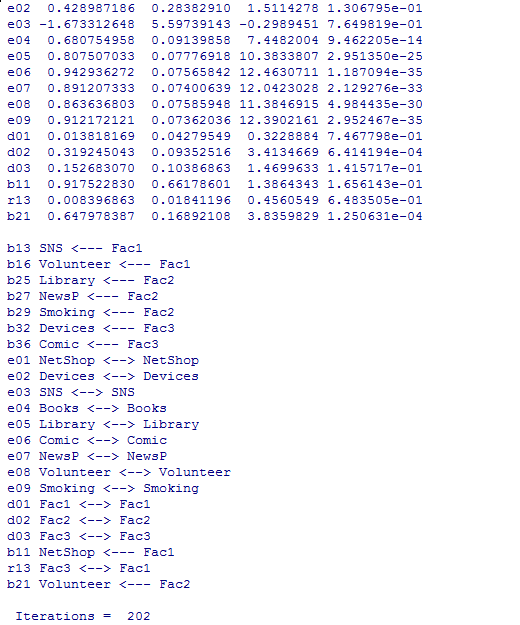
SNSの分散が負になったままであるので本来は余り良い分析結果ではないが，あくまで例示なのでこれ以上のモデルの検討は省略する。
構造方程式モデリングと云えば「パス・ダイアグラム」と云うイメージがあるので，取り敢えず簡単なグラフを描画する方法を紹介する。
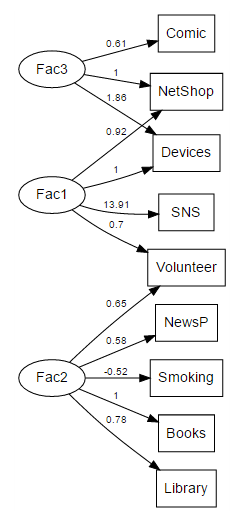
次の様に，図の調整の為のオプションを幾つか付けた上で，file=でdotファイルに出力する事が出来る。
digraph "result03" {
rankdir=TB;
size="12,10";
node [fontname="Times New Roman" fontsize=10 fillcolor="transparent" shape=box style=filled];
edge [fontname="Times New Roman" fontsize=10];
center=1;
{rank=min "Devices"}
{rank=max "Books"}
{rank=same "Fac1" "Fac2" "Fac3"}
{rank=same "SNS" "Devices" "NetShop" "Comic" "Smoking"}
{rank=same "Books" "Library" "NewsP" "Volunteer"}
"Fac1" [shape=ellipse]
"Fac2" [shape=ellipse]
"Fac3" [shape=ellipse]
"Devices" [fillcolor="transparent"]
"SNS" [fillcolor="transparent"]
"Volunteer" [fillcolor="transparent"]
"Books" [fillcolor="transparent"]
"Library" [fillcolor="transparent"]
"NewsP" [fillcolor="transparent"]
"Smoking" [fillcolor="transparent"]
"NetShop" [fillcolor="transparent"]
"Comic" [fillcolor="transparent"]
"Fac1" -> "Devices" [label="1" color=black penwidth=1.001];
"Fac1" -> "SNS" [label="13.909" color=black penwidth=1.001];
"Fac1" -> "Volunteer" [label="0.702" color=black penwidth=1.001];
"Fac2" -> "Books" [label="1" color=black penwidth=1.001];
"Fac2" -> "Library" [label="0.777" color=black penwidth=1.001];
"Fac2" -> "NewsP" [label="0.584" color=black penwidth=1.001];
"Fac2" -> "Smoking" [label="-0.525" color=black penwidth=1.001];
"Fac3" -> "NetShop" [label="1" color=black penwidth=1.001];
"Fac3" -> "Devices" [label="1.856" color=black penwidth=1.001];
"Fac3" -> "Comic" [label="0.611" color=black penwidth=1.001];
"NetShop" -> "NetShop" [label="0.82" dir=both color=black penwidth=1.001];
"Devices" -> "Devices" [label="0.429" dir=both color=black penwidth=1.001];
"SNS" -> "SNS" [label="-1.673" dir=both color=black penwidth=1.001];
"Books" -> "Books" [label="0.681" dir=both color=black penwidth=1.001];
"Library" -> "Library" [label="0.808" dir=both color=black penwidth=1.001];
"Comic" -> "Comic" [label="0.943" dir=both color=black penwidth=1.001];
"NewsP" -> "NewsP" [label="0.891" dir=both color=black penwidth=1.001];
"Volunteer" -> "Volunteer" [label="0.864" dir=both color=black penwidth=1.001];
"Smoking" -> "Smoking" [label="0.912" dir=both color=black penwidth=1.001];
"Fac1" -> "Fac1" [label="0.014" dir=both color=black penwidth=1.001];
"Fac2" -> "Fac2" [label="0.319" dir=both color=black penwidth=1.001];
"Fac3" -> "Fac3" [label="0.153" dir=both color=black penwidth=1.001];
"Fac1" -> "NetShop" [label="0.918" color=black penwidth=1.001];
"Fac1" -> "Fac3" [label="0.008" dir=both color=black penwidth=1.001];
"Fac2" -> "Volunteer" [label="0.648" color=black penwidth=1.001];
}
このCFA03.dotファイルを，GVeditなどのアプリケイションで読み込むと，図の調整や画像ファイルの出力が出来る。
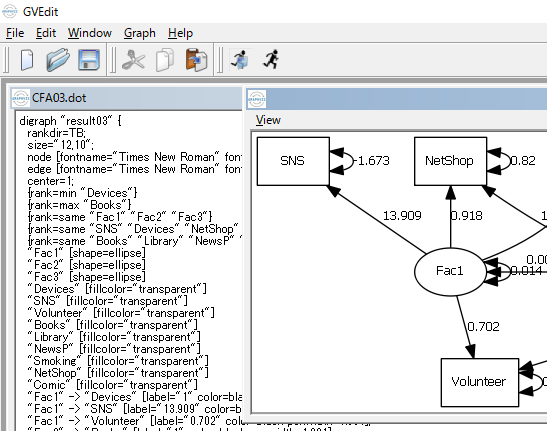
描画される画像（pngファイル）は以下である。
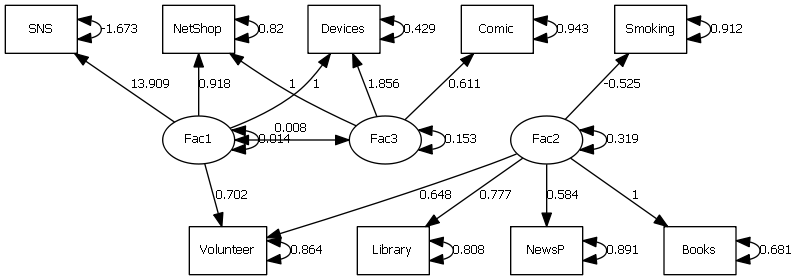
dotファイルの文法については下記のサイトなどが参考になる。
Watanabe Shin「Graphvizとdot言語でグラフを描く方法のまとめ」（2016年11月15日閲覧）
stdCoef( )関数にて，すべての変数の分散を1に標準化した上で求められる標準解を求めておこう。
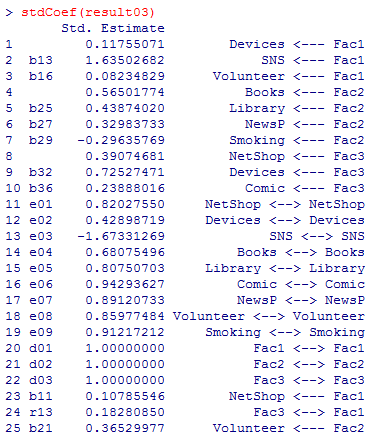
最後に，cfa( )関数を使って確証的因子モデルを書く方法も紹介しておく。
library(sem) # パッケイジの読み込み
# 下の行はSEMの代表的な適合度指標を表示させるためのオプション
opt <- options(fit.indices = c("GFI", "AGFI", "RMSEA", "AIC", "BIC"))
model01 <- specifyModel()
Fac1 -> Devices, NA, 1 # 第1因子から"Devices"変数へのパスを固定
Fac1 -> SNS, b13, NA # 第1因子から"SNS"変数へのパスは値を推定
Fac1 -> Volunteer, b16, NA
Fac2 -> Books, NA, 1 # それぞれの因子につき，どれか一つのパスは固定する。
Fac2 -> Library, b25, NA
Fac2 -> NewsP, b27, NA
Fac2 -> Smoking, b29, NA
Fac3 -> NetShop, NA, 1
Fac3 -> Devices, b32, NA
Fac3 -> Comic, b36, NA
NetShop <-> NetShop, e01, NA # "NetShop"変数の分散
Devices <-> Devices, e02, NA
SNS <-> SNS, e03, NA
Books <-> Books, e04, NA
Library <-> Library, e05, NA
Comic <-> Comic, e06, NA
NewsP <-> NewsP, e07, NA
Volunteer <-> Volunteer, e08, NA
Smoking <-> Smoking, e09, NA
Fac1 <-> Fac1, d01, NA # 第1因子の分散
Fac2 <-> Fac2, d02, NA
Fac3 <-> Fac3, d03, NA
result01 <- sem(model01, cor1<- cor(vars1), N=nrow(vars1)) # モデル，相関係数行列，ケース数を指定
summary(result01)
# 下の行はSEMの代表的な適合度指標を表示させるためのオプション
opt <- options(fit.indices = c("GFI", "AGFI", "RMSEA", "AIC", "BIC"))
model01 <- specifyModel()
Fac1 -> Devices, NA, 1 # 第1因子から"Devices"変数へのパスを固定
Fac1 -> SNS, b13, NA # 第1因子から"SNS"変数へのパスは値を推定
Fac1 -> Volunteer, b16, NA
Fac2 -> Books, NA, 1 # それぞれの因子につき，どれか一つのパスは固定する。
Fac2 -> Library, b25, NA
Fac2 -> NewsP, b27, NA
Fac2 -> Smoking, b29, NA
Fac3 -> NetShop, NA, 1
Fac3 -> Devices, b32, NA
Fac3 -> Comic, b36, NA
NetShop <-> NetShop, e01, NA # "NetShop"変数の分散
Devices <-> Devices, e02, NA
SNS <-> SNS, e03, NA
Books <-> Books, e04, NA
Library <-> Library, e05, NA
Comic <-> Comic, e06, NA
NewsP <-> NewsP, e07, NA
Volunteer <-> Volunteer, e08, NA
Smoking <-> Smoking, e09, NA
Fac1 <-> Fac1, d01, NA # 第1因子の分散
Fac2 <-> Fac2, d02, NA
Fac3 <-> Fac3, d03, NA
result01 <- sem(model01, cor1<- cor(vars1), N=nrow(vars1)) # モデル，相関係数行列，ケース数を指定
summary(result01)
modIndices( )関数を使って，どうしたらモデルが改善するかの示唆を得よう。
NetShop<-Fac1 から，第1因子からネットショッピングへのパスを追加し，Fac3<->Fac1 から，第1因子と第3因子に相関を追加すると良いと考えられる。
update( )関数を使ってmodel01を更新する。
model02 <- update(model01)
add, Fac1 -> NetShop, b11, NA
add, Fac1 <-> Fac3, r13, NA
result02 <- sem(model02, cor1, N=nrow(vars1))
summary(result02)
add, Fac1 -> NetShop, b11, NA
add, Fac1 <-> Fac3, r13, NA
result02 <- sem(model02, cor1, N=nrow(vars1))
summary(result02)
適合度指標は改善しているが，e03のSNSの分散がマイナスとなり，本来は不適切な解になっている。警告メッセージの「Negative parameter variances.」がそれを示している。
model03 <- update(model02)
add, Fac2 -> Volunteer, b21, NA
result03 <- sem(model03, cor1, N=nrow(vars1))
summary(result03)
add, Fac2 -> Volunteer, b21, NA
result03 <- sem(model03, cor1, N=nrow(vars1))
summary(result03)
SNSの分散が負になったままであるので本来は余り良い分析結果ではないが，あくまで例示なのでこれ以上のモデルの検討は省略する。
構造方程式モデリングと云えば「パス・ダイアグラム」と云うイメージがあるので，取り敢えず簡単なグラフを描画する方法を紹介する。
library(DiagrammeR)
pathDiagram(result03, edge.labels="values")
このコマンドを実行すると，ウェブ・ブラウザ上に次の様なグラフが出力される。ファイル形式は画像ファイルではなくhtmlファイルである。pathDiagram(result03, edge.labels="values")
次の様に，図の調整の為のオプションを幾つか付けた上で，file=でdotファイルに出力する事が出来る。
pathDiagram(result03, file="CFA03", output.type="dot", size=c(12,10),
ignore.double=FALSE, edge.labels="values", digits=3,
node.font=c("Times New Roman", 10),
edge.font=c("Times New Roman", 10),
min.rank="Devices", max.rank="Books", rank.direction="TB",
same.rank=c("Fac1, Fac2, Fac3",
"SNS, Devices, NetShop, Comic,Smoking",
"Books, Library, NewsP, Volunteer"))
このコマンドの結果，Rのworking directoryに出力されるCFA03.dotの中身は以下の様なテキストファイルである。ignore.double=FALSE, edge.labels="values", digits=3,
node.font=c("Times New Roman", 10),
edge.font=c("Times New Roman", 10),
min.rank="Devices", max.rank="Books", rank.direction="TB",
same.rank=c("Fac1, Fac2, Fac3",
"SNS, Devices, NetShop, Comic,Smoking",
"Books, Library, NewsP, Volunteer"))
digraph "result03" {
rankdir=TB;
size="12,10";
node [fontname="Times New Roman" fontsize=10 fillcolor="transparent" shape=box style=filled];
edge [fontname="Times New Roman" fontsize=10];
center=1;
{rank=min "Devices"}
{rank=max "Books"}
{rank=same "Fac1" "Fac2" "Fac3"}
{rank=same "SNS" "Devices" "NetShop" "Comic" "Smoking"}
{rank=same "Books" "Library" "NewsP" "Volunteer"}
"Fac1" [shape=ellipse]
"Fac2" [shape=ellipse]
"Fac3" [shape=ellipse]
"Devices" [fillcolor="transparent"]
"SNS" [fillcolor="transparent"]
"Volunteer" [fillcolor="transparent"]
"Books" [fillcolor="transparent"]
"Library" [fillcolor="transparent"]
"NewsP" [fillcolor="transparent"]
"Smoking" [fillcolor="transparent"]
"NetShop" [fillcolor="transparent"]
"Comic" [fillcolor="transparent"]
"Fac1" -> "Devices" [label="1" color=black penwidth=1.001];
"Fac1" -> "SNS" [label="13.909" color=black penwidth=1.001];
"Fac1" -> "Volunteer" [label="0.702" color=black penwidth=1.001];
"Fac2" -> "Books" [label="1" color=black penwidth=1.001];
"Fac2" -> "Library" [label="0.777" color=black penwidth=1.001];
"Fac2" -> "NewsP" [label="0.584" color=black penwidth=1.001];
"Fac2" -> "Smoking" [label="-0.525" color=black penwidth=1.001];
"Fac3" -> "NetShop" [label="1" color=black penwidth=1.001];
"Fac3" -> "Devices" [label="1.856" color=black penwidth=1.001];
"Fac3" -> "Comic" [label="0.611" color=black penwidth=1.001];
"NetShop" -> "NetShop" [label="0.82" dir=both color=black penwidth=1.001];
"Devices" -> "Devices" [label="0.429" dir=both color=black penwidth=1.001];
"SNS" -> "SNS" [label="-1.673" dir=both color=black penwidth=1.001];
"Books" -> "Books" [label="0.681" dir=both color=black penwidth=1.001];
"Library" -> "Library" [label="0.808" dir=both color=black penwidth=1.001];
"Comic" -> "Comic" [label="0.943" dir=both color=black penwidth=1.001];
"NewsP" -> "NewsP" [label="0.891" dir=both color=black penwidth=1.001];
"Volunteer" -> "Volunteer" [label="0.864" dir=both color=black penwidth=1.001];
"Smoking" -> "Smoking" [label="0.912" dir=both color=black penwidth=1.001];
"Fac1" -> "Fac1" [label="0.014" dir=both color=black penwidth=1.001];
"Fac2" -> "Fac2" [label="0.319" dir=both color=black penwidth=1.001];
"Fac3" -> "Fac3" [label="0.153" dir=both color=black penwidth=1.001];
"Fac1" -> "NetShop" [label="0.918" color=black penwidth=1.001];
"Fac1" -> "Fac3" [label="0.008" dir=both color=black penwidth=1.001];
"Fac2" -> "Volunteer" [label="0.648" color=black penwidth=1.001];
}
このCFA03.dotファイルを，GVeditなどのアプリケイションで読み込むと，図の調整や画像ファイルの出力が出来る。
描画される画像（pngファイル）は以下である。
dotファイルの文法については下記のサイトなどが参考になる。
Watanabe Shin「Graphvizとdot言語でグラフを描く方法のまとめ」（2016年11月15日閲覧）
stdCoef( )関数にて，すべての変数の分散を1に標準化した上で求められる標準解を求めておこう。
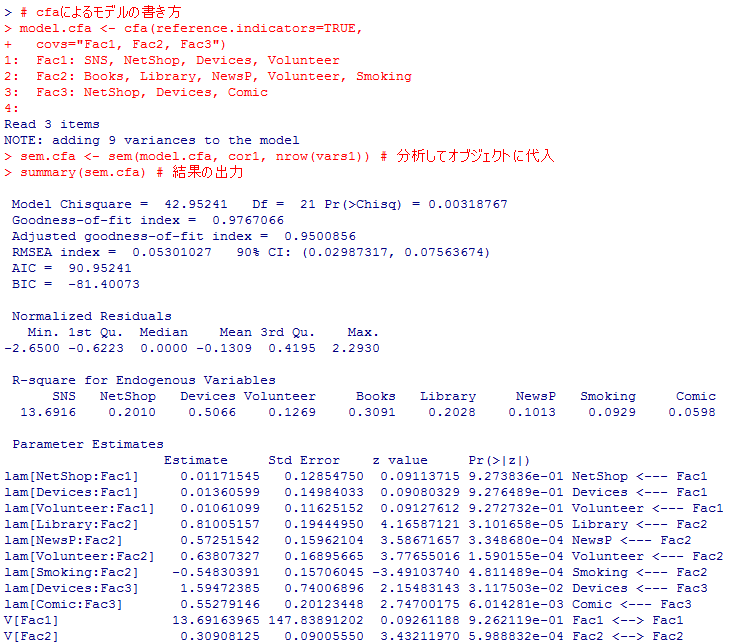
最後に，cfa( )関数を使って確証的因子モデルを書く方法も紹介しておく。
# cfaによるモデルの書き方
model.cfa <- cfa(reference.indicators=TRUE,
covs="Fac1, Fac2, Fac3")
Fac1: SNS, NetShop, Devices, Volunteer
Fac2: Books, Library, NewsP, Volunteer, Smoking
Fac3: NetShop, Devices, Comic
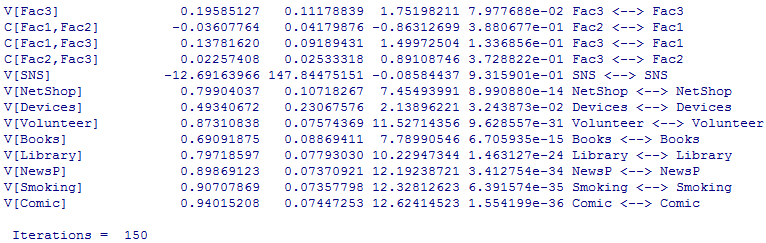
sem.cfa <- sem(model.cfa, cor1, nrow(vars1)) # 分析してオブジェクトに代入
summary(sem.cfa) # 結果の出力
stdCoef(sem.cfa) # 標準化解を求める。
model.cfa <- cfa(reference.indicators=TRUE,
covs="Fac1, Fac2, Fac3")
Fac1: SNS, NetShop, Devices, Volunteer
Fac2: Books, Library, NewsP, Volunteer, Smoking
Fac3: NetShop, Devices, Comic
sem.cfa <- sem(model.cfa, cor1, nrow(vars1)) # 分析してオブジェクトに代入
summary(sem.cfa) # 結果の出力
stdCoef(sem.cfa) # 標準化解を求める。
発展1-2 構造方程式モデリングとパス解析(path analysis)
男性に限定した完備ケース分析にて，年齢で教育年数を説明し，年齢と教育年数で収入を説明する（古典的）パス解析を行う。
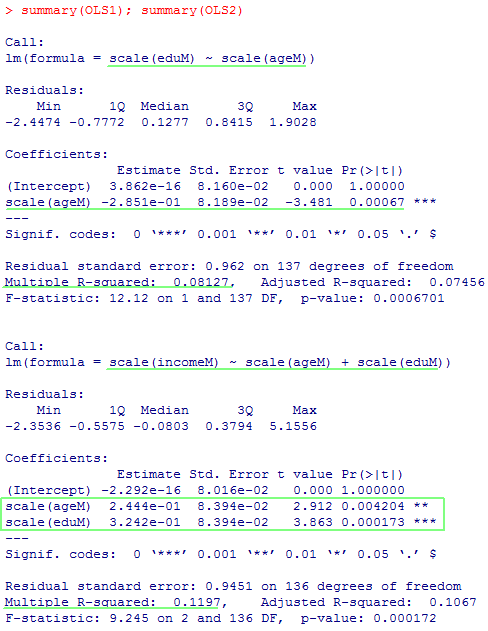
この結果をGVeditでパス・ダイアグラムに描いたのが下記である。
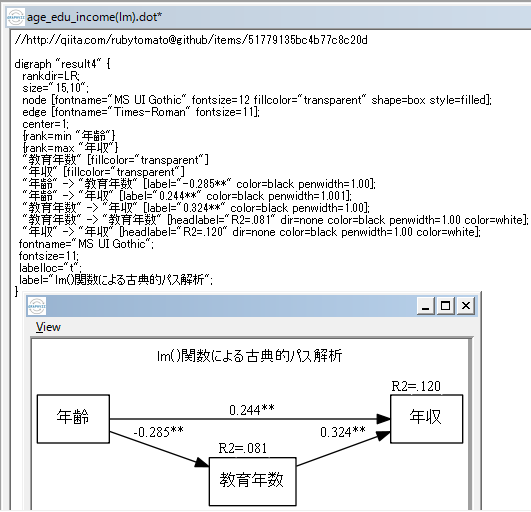
このパス解析を，SEMを使って実行してみよう。
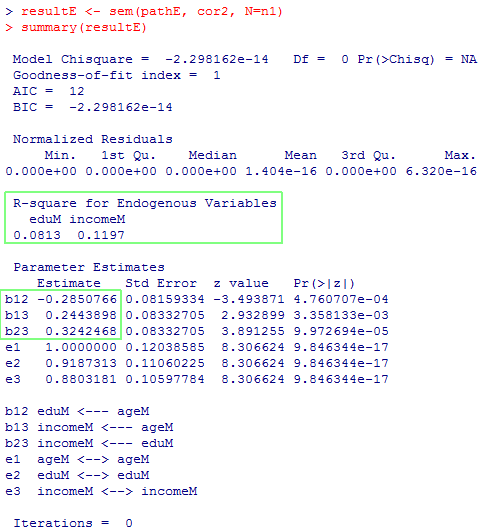
こうして記述したモデルをsem( )関数に与えて構造方程式モデリングの分析を行う。pathEの部分をpathMとしても全く同一の出力である。
# 各変数を男性に限定し，完備ケース分析とする
complete <- complete.cases(data01$age, data01$edu, data01$income) & data01$sex == 1
ageM <- data01$age[complete]
eduM <- data01$edu[complete]
incomeM <- data01$income[complete]
OLS1 <- lm(scale(eduM) ~ scale(ageM))
OLS2 <- lm(scale(incomeM) ~scale(ageM) + scale(eduM))
summary(OLS1); summary(OLS2)
complete <- complete.cases(data01$age, data01$edu, data01$income) & data01$sex == 1
ageM <- data01$age[complete]
eduM <- data01$edu[complete]
incomeM <- data01$income[complete]
OLS1 <- lm(scale(eduM) ~ scale(ageM))
OLS2 <- lm(scale(incomeM) ~scale(ageM) + scale(eduM))
summary(OLS1); summary(OLS2)
この結果をGVeditでパス・ダイアグラムに描いたのが下記である。
このパス解析を，SEMを使って実行してみよう。
n1 <- length(ageM) # SEMの為にケース数を保存
cor2 <- cor(cbind(ageM, eduM, incomeM)) # SEMの為に相関係数行列を保存
pathE <- specifyEquations() # 記法その1
eduM = b12*ageM
incomeM = b13*ageM + b23*eduM
V(ageM) = e1
V(eduM) = e2
V(incomeM) = e3
pathM <- specifyModel() # 記法その2
ageM -> eduM, b12, NA
ageM -> incomeM, b13, NA
eduM -> incomeM, b23, NA
ageM <-> ageM, e1, NA
eduM <-> eduM, e2, NA
incomeM <-> incomeM, e3, NA
print(pathE) # 結果の同一性の確認
print(pathM)
cor2 <- cor(cbind(ageM, eduM, incomeM)) # SEMの為に相関係数行列を保存
pathE <- specifyEquations() # 記法その1
eduM = b12*ageM
incomeM = b13*ageM + b23*eduM
V(ageM) = e1
V(eduM) = e2
V(incomeM) = e3
pathM <- specifyModel() # 記法その2
ageM -> eduM, b12, NA
ageM -> incomeM, b13, NA
eduM -> incomeM, b23, NA
ageM <-> ageM, e1, NA
eduM <-> eduM, e2, NA
incomeM <-> incomeM, e3, NA
print(pathE) # 結果の同一性の確認
print(pathM)
こうして記述したモデルをsem( )関数に与えて構造方程式モデリングの分析を行う。pathEの部分をpathMとしても全く同一の出力である。
resultE <- sem(pathE, cor2, N=n1)
summary(resultE)
summary(resultE)
Copyright (C) 2016-2017 SUGINO Isamu All Rights Reserved. design by tempnate