杉野 勇 (SUGINO Isamu) お茶の水女子大学・人間発達科学専攻・応用社会学コース担当
『入門・社会統計学』サポートウェブ |
|
 第6章 2群の母平均の差のt検定
第6章 2群の母平均の差のt検定
1-1 2群の母分散が等しいかどうかのF検定(F test)
演習用データの男女別幸福度の平均と不偏分散,有効ケース数の表が本文にある。これを求める方法を示しておく。まずはデータを準備する部分を再掲しておく。本文では簡便化の為に幸福度の変数名を元のq1700のままで書いているが,実際には11という値を欠損値NAにしなければならないので,その欠損値処理をした変数を新たにq1700bとしている。


等分散性の検定は次のように行う。本文のF分布グラフを描くスクリプトをその後に挙げる。
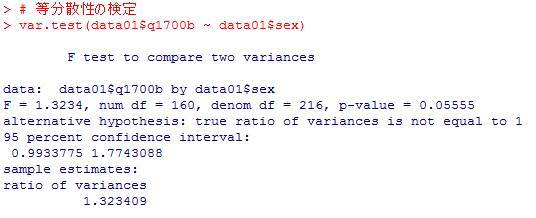
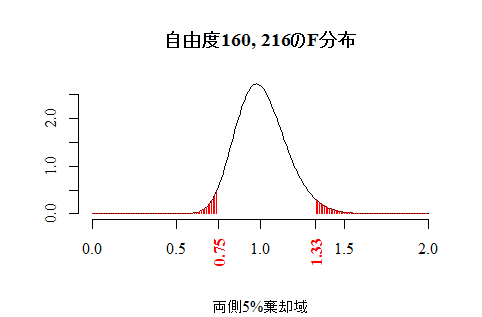
共通の母分散の推定値を計算するには以下の様にすると良い。不偏分散と自由度をいずれも長さ2のヴェクトルとして格納すると,計算式はすっきりとしたものになる。因みにこの場合の結果は [1] 3.510335 となる。
data01 <- read.csv("practice.csv") # 先にworking directoryにデータファイルを置いておく
names(data01) # 読み込んだデータフレイムの中の変数名を確認
# まず最初に使用する変数の度数分布表を確認しておく。欠損値もあれば表示させる。
table(data01$sex, useNA="ifany")
table(data01$q1700, useNA="ifany")
# q1700=11は「わからない」で欠損値NAとすべきなので,新変数q1700bを作成。
data01$q1700b <- c(0:10)[data01$q1700+1] # 変数のリコード法にはやや工夫をしている。
table(data01$q1700b, useNA="always") # 変換の結果を確認
names(data01) # 読み込んだデータフレイムの中の変数名を確認
# まず最初に使用する変数の度数分布表を確認しておく。欠損値もあれば表示させる。
table(data01$sex, useNA="ifany")
table(data01$q1700, useNA="ifany")
# q1700=11は「わからない」で欠損値NAとすべきなので,新変数q1700bを作成。
data01$q1700b <- c(0:10)[data01$q1700+1] # 変数のリコード法にはやや工夫をしている。
table(data01$q1700b, useNA="always") # 変換の結果を確認

# 男女別の幸福度の標本平均,不偏分散,有効ケース数
by(data01$q1700b, data01$sex, mean, na.rm=T)
by(data01$q1700b, data01$sex, var, na.rm=T)
by(data01$q1700b, data01$sex, function(x) sum(!is.na(x)))
# tapply()関数でも同様にできる。
tapply(data01$q1700b, data01$sex, mean, na.rm=T)
tapply(data01$q1700b, data01$sex, var, na.rm=T)
tapply(data01$q1700b, data01$sex, function(x) sum(!is.na(x)))
by(data01$q1700b, data01$sex, mean, na.rm=T)
by(data01$q1700b, data01$sex, var, na.rm=T)
by(data01$q1700b, data01$sex, function(x) sum(!is.na(x)))
# tapply()関数でも同様にできる。
tapply(data01$q1700b, data01$sex, mean, na.rm=T)
tapply(data01$q1700b, data01$sex, var, na.rm=T)
tapply(data01$q1700b, data01$sex, function(x) sum(!is.na(x)))

等分散性の検定は次のように行う。本文のF分布グラフを描くスクリプトをその後に挙げる。

df0 <- by(data01$q1700b, data01$sex, function(x) sum(!is.na(x)))-1 # 自由度ヴェクトル
p0 <- .05 # 有意水準
plot(x <- seq(0,2,by=.01), df(x, df0[1], df0[2]), type="l", bty="n",
xlab="", ylab="", family="serif",
main=sprintf("自由度%d, %dのF分布", df0[1], df0[2]),
sub=sprintf("両側%d%%棄却域", p0*100))
segments(x1 <- c(seq(0, qf(p0/2, df0[1], df0[2]), by=.01), seq(qf(1-p0/2, df0[1], df0[2]), 2, by=.01)), 0,
x1, df(x1, df0[1], df0[2]), col="red")
axis(side=1, at=round(c(qf(p0/2, df0[1], df0[2]), qf(1-p0/2, df0[1], df0[2])), 2),
las=2, family="serif", font=2, col.axis="red")
p0 <- .05 # 有意水準
plot(x <- seq(0,2,by=.01), df(x, df0[1], df0[2]), type="l", bty="n",
xlab="", ylab="", family="serif",
main=sprintf("自由度%d, %dのF分布", df0[1], df0[2]),
sub=sprintf("両側%d%%棄却域", p0*100))
segments(x1 <- c(seq(0, qf(p0/2, df0[1], df0[2]), by=.01), seq(qf(1-p0/2, df0[1], df0[2]), 2, by=.01)), 0,
x1, df(x1, df0[1], df0[2]), col="red")
axis(side=1, at=round(c(qf(p0/2, df0[1], df0[2]), qf(1-p0/2, df0[1], df0[2])), 2),
las=2, family="serif", font=2, col.axis="red")

共通の母分散の推定値を計算するには以下の様にすると良い。不偏分散と自由度をいずれも長さ2のヴェクトルとして格納すると,計算式はすっきりとしたものになる。因みにこの場合の結果は [1] 3.510335 となる。
var0 <- by(data01$q1700b, data01$sex, var, na.rm=T)
sum(var0*df0)/sum(df0)
sum(var0*df0)/sum(df0)
1-2 母分散が等しい2群の母平均差のt検定
Studentのt検定のスクリプトとその出力を纏めて示す。
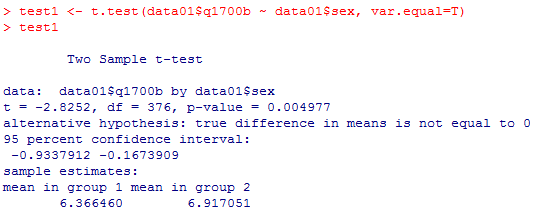
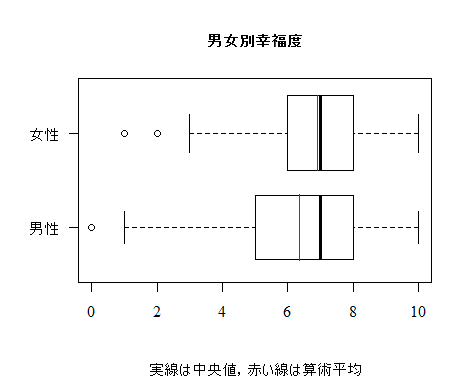
以下は,本文のような箱ひげ図を描くスクリプトである。少し変えた部分もある。
 この例題をベイズ統計学的手法で計算した例を,このサポートウェブの〔付録〕2-1に示しています。
この例題をベイズ統計学的手法で計算した例を,このサポートウェブの〔付録〕2-1に示しています。

以下は,本文のような箱ひげ図を描くスクリプトである。少し変えた部分もある。
boxplot(data01$q1700b ~ data01$sex, las=1, cex.main=1,
main="男女別幸福度", sub="実線は中央値,赤い線は算術平均", varwidth=T,
names=c("男性","女性"), par(family="serif"), horizontal=T)
m0 <- by(data01$q1700b, data01$sex, mean, na.rm=T)
segments(m0[1], 0.65, m0[1], 1.35, col="red")
segments(m0[2], 1.6, m0[2], 2.4, col="red")
main="男女別幸福度", sub="実線は中央値,赤い線は算術平均", varwidth=T,
names=c("男性","女性"), par(family="serif"), horizontal=T)
m0 <- by(data01$q1700b, data01$sex, mean, na.rm=T)
segments(m0[1], 0.65, m0[1], 1.35, col="red")
segments(m0[2], 1.6, m0[2], 2.4, col="red")

 この例題をベイズ統計学的手法で計算した例を,このサポートウェブの〔付録〕2-1に示しています。
この例題をベイズ統計学的手法で計算した例を,このサポートウェブの〔付録〕2-1に示しています。
1-3 母分散が異なる2群の母平均差のウェルチ検定(Welch test)
本文では省略している部分も一つ一つ確認しながら説明してゆこう。
まずは世帯年収fincomeの度数分布表,男女別の平均や分散,有効ケース数の出力,そして等分散性のF検定を行おう。

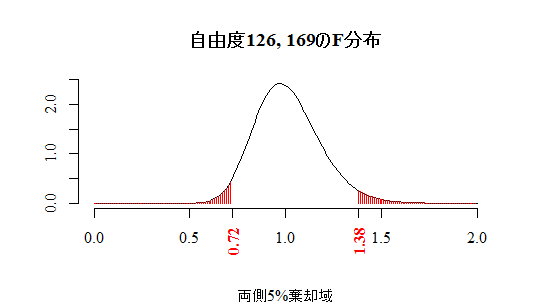
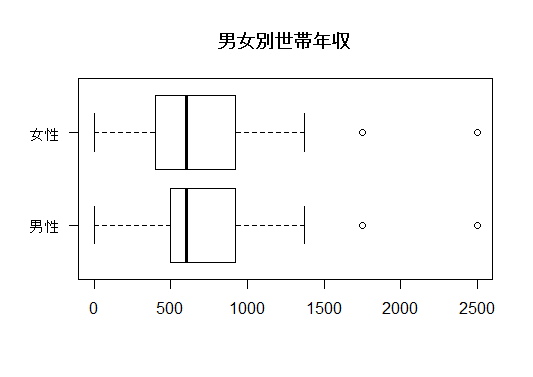
男女の世帯年収の分布を,上の1-2でも紹介した箱ひげ図を用いて視覚的に確認しておこう。
等分散性が棄却されたので,ウェルチの検定を行う。等分散ではないというオプション "var.equal=FALSE" を指定してt.test( )関数を用いるのだが,このオプションを単に省略すれば,Rのt.test( )関数はデフォルトでウェルチの検定を行うようになっている。
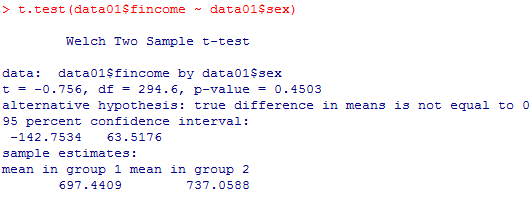
ウェルチ検定のt統計量の絶対値は.756と小さく,有意確率は45%もある。つまり,ゼロ仮説が正しく,母平均は男女で等しいとしても,標本でたまたまこの程度の差が生じることはよくあることであり,(ゼロ仮説を含めて)何も疑うべきものはないということである。母平均の差の95%信頼区間はマイナスからプラスに広がっており,0を間に含んでいる。ゼロ仮説の検定が5%で有意にならない(否定できない)ことと一致している。
 〔付録〕3-2では,RとStanでWelch検定と等価な分析を行う方法を紹介しています。
〔付録〕3-2では,RとStanでWelch検定と等価な分析を行う方法を紹介しています。
まずは世帯年収fincomeの度数分布表,男女別の平均や分散,有効ケース数の出力,そして等分散性のF検定を行おう。
table(data01$fincome, useNA="always")
by(data01$fincome, data01$sex, mean, na.rm=T)
by(data01$fincome, data01$sex, var, na.rm=T)
df0 <- by(data01$fincome, data01$sex, function(x) sum(!is.na(x))); df0
var.test(data01$fincome ~ data01$sex)
by(data01$fincome, data01$sex, mean, na.rm=T)
by(data01$fincome, data01$sex, var, na.rm=T)
df0 <- by(data01$fincome, data01$sex, function(x) sum(!is.na(x))); df0
var.test(data01$fincome ~ data01$sex)

p0 <- .05 # 有意水準
plot(x <- seq(0,2,by=.01), df(x, df0[1]-1, df0[2]-1), type="l", bty="n",
xlab="", ylab="", family="serif",
main=sprintf("自由度%d, %dのF分布", df0[1]-1, df0[2]-1),
sub=sprintf("両側%d%%棄却域", p0*100))
segments(x1 <- c(seq(0, qf(p0/2, df0[1]-1, df0[2]-1), by=.01),
seq(qf(1-p0/2, df0[1]-1, df0[2]-1), 2, by=.01)), 0,
x1, df(x1, df0[1]-1, df0[2]-1), col="red")
axis(side=1, las=2, family="serif", font=2, col.axis="red")
at=round(c(qf(p0/2, df0[1]-1, df0[2]-1), qf(1-p0/2, df0[1]-1, df0[2]-1)), 2),
plot(x <- seq(0,2,by=.01), df(x, df0[1]-1, df0[2]-1), type="l", bty="n",
xlab="", ylab="", family="serif",
main=sprintf("自由度%d, %dのF分布", df0[1]-1, df0[2]-1),
sub=sprintf("両側%d%%棄却域", p0*100))
segments(x1 <- c(seq(0, qf(p0/2, df0[1]-1, df0[2]-1), by=.01),
seq(qf(1-p0/2, df0[1]-1, df0[2]-1), 2, by=.01)), 0,
x1, df(x1, df0[1]-1, df0[2]-1), col="red")
axis(side=1, las=2, family="serif", font=2, col.axis="red")
at=round(c(qf(p0/2, df0[1]-1, df0[2]-1), qf(1-p0/2, df0[1]-1, df0[2]-1)), 2),

男女の世帯年収の分布を,上の1-2でも紹介した箱ひげ図を用いて視覚的に確認しておこう。
boxplot(data01$fincome ~ data01$sex, horizontal=T, las=1,
names=c("男性", "女性"), main="男女別世帯年収")
names=c("男性", "女性"), main="男女別世帯年収")

等分散性が棄却されたので,ウェルチの検定を行う。等分散ではないというオプション "var.equal=FALSE" を指定してt.test( )関数を用いるのだが,このオプションを単に省略すれば,Rのt.test( )関数はデフォルトでウェルチの検定を行うようになっている。

ウェルチ検定のt統計量の絶対値は.756と小さく,有意確率は45%もある。つまり,ゼロ仮説が正しく,母平均は男女で等しいとしても,標本でたまたまこの程度の差が生じることはよくあることであり,(ゼロ仮説を含めて)何も疑うべきものはないということである。母平均の差の95%信頼区間はマイナスからプラスに広がっており,0を間に含んでいる。ゼロ仮説の検定が5%で有意にならない(否定できない)ことと一致している。
 〔付録〕3-2では,RとStanでWelch検定と等価な分析を行う方法を紹介しています。
〔付録〕3-2では,RとStanでWelch検定と等価な分析を行う方法を紹介しています。
2-1 母平均の差の区間推定
本文同様,男性平均−女性平均の母平均差の95%信頼区間を,式に従って求め,それと検定結果の出力が一致する事を確認しよう。

1-3のウェルチの検定はどうなるだろうか。やや難しく見えるが,以下の計算で求められる。最後にウェルチの検定の結果を示して,信頼区間が一致している事を確認する。

m0 <- by(data01$q1700b, data01$sex, mean, na.rm=T)
var0 <- by(data01$q1700b, data01$sex, var, na.rm=T)
n0 <- by(data01$q1700b, data01$sex, function(x) sum(!is.na(x)))
# 男女の幸福度の標本平均差
m_diff <- m0[1] - m0[2]
# 共通の母標準偏差の推定値
sigma <- sqrt(sum(var0*(n0 - 1))/(sum(n0)-2))
# 母平均差の95%信頼区間下限値
m_diff - qt(.975, df=sum(n0)-2)*sigma*sqrt(sum(1/n0))
# 信頼区間上限値
m_diff - qt(.025, df=sum(n0)-2)*sigma*sqrt(sum(1/n0))
# t検定の結果
test1 <- t.test(data01$q1700b ~ data01$sex, var.equal=T)
test1
var0 <- by(data01$q1700b, data01$sex, var, na.rm=T)
n0 <- by(data01$q1700b, data01$sex, function(x) sum(!is.na(x)))
# 男女の幸福度の標本平均差
m_diff <- m0[1] - m0[2]
# 共通の母標準偏差の推定値
sigma <- sqrt(sum(var0*(n0 - 1))/(sum(n0)-2))
# 母平均差の95%信頼区間下限値
m_diff - qt(.975, df=sum(n0)-2)*sigma*sqrt(sum(1/n0))
# 信頼区間上限値
m_diff - qt(.025, df=sum(n0)-2)*sigma*sqrt(sum(1/n0))
# t検定の結果
test1 <- t.test(data01$q1700b ~ data01$sex, var.equal=T)
test1

1-3のウェルチの検定はどうなるだろうか。やや難しく見えるが,以下の計算で求められる。最後にウェルチの検定の結果を示して,信頼区間が一致している事を確認する。
m0 <- by(data01$fincome, data01$sex, mean, na.rm=T)
var0 <- by(data01$fincome, data01$sex, var, na.rm=T)
n0 <- by(data01$fincome, data01$sex, function(x) sum(!is.na(x)))
m_diff <- m0[1] - m0[2] # 男女の世帯収入の標本平均差
se0 <- sqrt(sum(var0/n0)) # 標準誤差推定値
# ウェルチ検定の自由度計算
df1 <- prod(n0-1)*sum(var0/n0)^2/((n0[2]-1)*(var0[1]/n0[1])^2+(n0[1]-1)*(var0[2]/n0[2])^2)
m_diff - qt(.975, df=df1)*se0 # 母平均差の95%信頼区間下限値
m_diff - qt(.025, df=df1)*se0 # 信頼区間上限値
# Welch検定の結果と比較する
test2 <- t.test(data01$fincome ~ data01$sex); test2
var0 <- by(data01$fincome, data01$sex, var, na.rm=T)
n0 <- by(data01$fincome, data01$sex, function(x) sum(!is.na(x)))
m_diff <- m0[1] - m0[2] # 男女の世帯収入の標本平均差
se0 <- sqrt(sum(var0/n0)) # 標準誤差推定値
# ウェルチ検定の自由度計算
df1 <- prod(n0-1)*sum(var0/n0)^2/((n0[2]-1)*(var0[1]/n0[1])^2+(n0[1]-1)*(var0[2]/n0[2])^2)
m_diff - qt(.975, df=df1)*se0 # 母平均差の95%信頼区間下限値
m_diff - qt(.025, df=df1)*se0 # 信頼区間上限値
# Welch検定の結果と比較する
test2 <- t.test(data01$fincome ~ data01$sex); test2

2-2 効果サイズ(effect size)と検定力
1-1〜1-2の幸福度の男女差の例で効果サイズを考える。テキスト本文や上記スクリプトとは少し違うスクリプトで計算してみる。様々な方法で同じ様な事が出来ると云う事を読み取って欲しい。

次に後半の結果を示す。各群でケース数が異なるので,小さい方のサンプルサイズ,大きい方のサンプルサイズ,算術平均,幾何平均の4通りのサンプルサイズをヴェクトルとして使用した。

4通りのサンプルサイズそれぞれに対応した検定力が出力されている。本文の結果ともほぼ一致している。
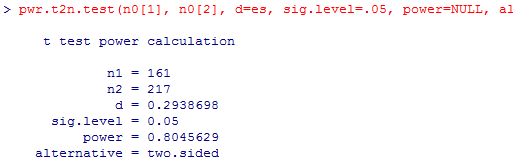
以上の検定力や効果量の計算はいずれも二群の母分散が等しいと仮定した話であった。次に,二群の母分散が等しいとは言えない場合について述べる。
本文でも述べた様に,「平均的な標準偏差」を計算して利用する方法と,いずれか一方の標準偏差(分散)を「基準」として利用する方法がある。男女別の世帯年収fincomeで例示しよう。

男性においてよりも女性において世帯年収の標準偏差が大きい。大きな標準偏差を「基準」として用いるほど,それだけ偶然による変動のリスクが高まり,効果サイズは小さくなる(結果出力のd=の欄)。効果サイズが小さくなれば,小さな効果を検出するのは難しくなるので,検定力も下がる(power=の欄)。
しかしいずれにしても効果サイズは小さく,検定力は15%にも満たない。検定力を.80(80%)として,このサンプルサイズで検定できる効果サイズを求めると,約0.33は必要である事が分かる。
逆に,.085程度の小さな効果サイズを有意水準.05,検定力.80で検定しようと思うとどの程度の大きさの標本が必要かを計算してみよう。
まずは,二群のサイズが等しい場合を標準のpower.t.test( )関数で計算する。
その次に,二群のサイズが異なる場合をpwr.t2n.test( )関数で計算する。

二群のサイズが等しい場合には,それぞれの群のサイズが2174人,合計で4348人が必要である事が分かる。
片方の群のサイズが小さい程,もう一つの群のサイズがかなり大きい事が必要になる。

MBESSパッケイジのconf.limits.nct( )関数は,第4章で解説した,非心t分布の非心パラメタの信頼区間を求める関数である。ここでは追加パッケイジの新規インストールから説明して行こう。インストール中の画面を一部抜粋して掲示する。

…(中略)…
…(中略)…


m0 <- by(data01$q1700b, data01$sex, mean, na.rm=T); m0
v0 <- by(data01$q1700b, data01$sex, var, na.rm=T); v0
n0 <- by(data01$q1700b, data01$sex, function(x) sum(!is.na(x))); n0
m_diff <- diff(rev(m0)); m_diff # 男女の幸福度の標本平均差
sigma <- sqrt(sum(v0*(n0 - 1))/(sum(n0)-2)) # 共通の母標準偏差の推定値
es <- m_diff/sigma; es # 標本効果サイズ
# 4通りの標本サイズ
n1 <- c(n0, floor(sum(n0)/2), floor(sqrt(prod(n0)))); n1
power.t.test(n=n1, sd=sigma, delta=m_diff, sig.level=.05, power=NULL, type="two.sample")
まずは前半の結果である。各平均,分散,ケース数といった基本情報を確認し,標本平均の差,標本効果サイズを求めた。v0 <- by(data01$q1700b, data01$sex, var, na.rm=T); v0
n0 <- by(data01$q1700b, data01$sex, function(x) sum(!is.na(x))); n0
m_diff <- diff(rev(m0)); m_diff # 男女の幸福度の標本平均差
sigma <- sqrt(sum(v0*(n0 - 1))/(sum(n0)-2)) # 共通の母標準偏差の推定値
es <- m_diff/sigma; es # 標本効果サイズ
# 4通りの標本サイズ
n1 <- c(n0, floor(sum(n0)/2), floor(sqrt(prod(n0)))); n1
power.t.test(n=n1, sd=sigma, delta=m_diff, sig.level=.05, power=NULL, type="two.sample")

次に後半の結果を示す。各群でケース数が異なるので,小さい方のサンプルサイズ,大きい方のサンプルサイズ,算術平均,幾何平均の4通りのサンプルサイズをヴェクトルとして使用した。

4通りのサンプルサイズそれぞれに対応した検定力が出力されている。本文の結果ともほぼ一致している。
パッケイジ"pwr"のpwr.t2n.test( )関数
二群のサイズが異なる場合の検定力分析を正しく行う為の追加パッケイジ"pwr"とその関数pwr.t2n.test( )を使用してみよう。これも本文とはスクリプトが少し異なるので注意してほしい。PCにpwrをインストールした事が無い場合は,install.packages("pwr", repos="https://cran.ism.ac.jp")を一度だけ実行しておく。
library(pwr) # インストールした"pwr"パッケージを有効化する
pwr.t2n.test(n0[1], n0[2], d=es, sig.level=.05, power=NULL, alternative="two.sided")
pwr.t2n.test(n0[1], n0[2], d=es, sig.level=.05, power=NULL, alternative="two.sided")

以上の検定力や効果量の計算はいずれも二群の母分散が等しいと仮定した話であった。次に,二群の母分散が等しいとは言えない場合について述べる。
本文でも述べた様に,「平均的な標準偏差」を計算して利用する方法と,いずれか一方の標準偏差(分散)を「基準」として利用する方法がある。男女別の世帯年収fincomeで例示しよう。
m0 <- by(data01$fincome, data01$sex, mean, na.rm=T)
v0 <- by(data01$fincome, data01$sex, var, na.rm=T)
n0 <- by(data01$fincome, data01$sex, function(x) sum(!is.na(x)))
m0
# 平均的な不偏分散を計算して,その平方根を平均的な標準偏差とする。
sd0 <- sqrt(sum(v0*(n0-1))/sum(n0-1))
sd1 <- c(sqrt(v0), sd0)
es1 <- diff(rev(m0))/sd1
sd1
pwr.t2n.test(n0[1], n0[2], d=es1, sig.level=.05, power=NULL, alternative="two.sided")
v0 <- by(data01$fincome, data01$sex, var, na.rm=T)
n0 <- by(data01$fincome, data01$sex, function(x) sum(!is.na(x)))
m0
# 平均的な不偏分散を計算して,その平方根を平均的な標準偏差とする。
sd0 <- sqrt(sum(v0*(n0-1))/sum(n0-1))
sd1 <- c(sqrt(v0), sd0)
es1 <- diff(rev(m0))/sd1
sd1
pwr.t2n.test(n0[1], n0[2], d=es1, sig.level=.05, power=NULL, alternative="two.sided")

男性においてよりも女性において世帯年収の標準偏差が大きい。大きな標準偏差を「基準」として用いるほど,それだけ偶然による変動のリスクが高まり,効果サイズは小さくなる(結果出力のd=の欄)。効果サイズが小さくなれば,小さな効果を検出するのは難しくなるので,検定力も下がる(power=の欄)。
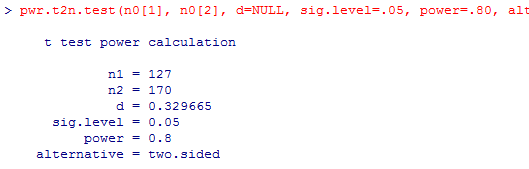
しかしいずれにしても効果サイズは小さく,検定力は15%にも満たない。検定力を.80(80%)として,このサンプルサイズで検定できる効果サイズを求めると,約0.33は必要である事が分かる。
pwr.t2n.test(n0[1], n0[2], d=NULL, sig.level=.05, power=.80, alternative="two.sided")

逆に,.085程度の小さな効果サイズを有意水準.05,検定力.80で検定しようと思うとどの程度の大きさの標本が必要かを計算してみよう。
まずは,二群のサイズが等しい場合を標準のpower.t.test( )関数で計算する。
その次に,二群のサイズが異なる場合をpwr.t2n.test( )関数で計算する。
# 標準の検定力関数
power.t.test(n=NULL, d=.085, sig.level=.05, power=.80, alternative="two.sided")
# パッケイジpwr中のpwr.t2n.test( )関数
# 両方の標本サイズを同時に空欄には出来ないので,片方の標本サイズは3通りくらいで指定する
pwr.t2n.test(n1=1100, n2=NULL, d=.085, sig.level=.05, power=.80, alternative="two.sided")
pwr.t2n.test(n1=1500, n2=NULL, d=.085, sig.level=.05, power=.80, alternative="two.sided")
pwr.t2n.test(n1=2100, n2=NULL, d=.085, sig.level=.05, power=.80, alternative="two.sided")
power.t.test(n=NULL, d=.085, sig.level=.05, power=.80, alternative="two.sided")
# パッケイジpwr中のpwr.t2n.test( )関数
# 両方の標本サイズを同時に空欄には出来ないので,片方の標本サイズは3通りくらいで指定する
pwr.t2n.test(n1=1100, n2=NULL, d=.085, sig.level=.05, power=.80, alternative="two.sided")
pwr.t2n.test(n1=1500, n2=NULL, d=.085, sig.level=.05, power=.80, alternative="two.sided")
pwr.t2n.test(n1=2100, n2=NULL, d=.085, sig.level=.05, power=.80, alternative="two.sided")

二群のサイズが等しい場合には,それぞれの群のサイズが2174人,合計で4348人が必要である事が分かる。
片方の群のサイズが小さい程,もう一つの群のサイズがかなり大きい事が必要になる。

"MBESS"パッケイジのconf.limits.nct( )関数
最後に,標本効果サイズから母効果サイズの信頼区間を求める一つの方法を紹介しよう。MBESSパッケイジのconf.limits.nct( )関数は,第4章で解説した,非心t分布の非心パラメタの信頼区間を求める関数である。ここでは追加パッケイジの新規インストールから説明して行こう。インストール中の画面を一部抜粋して掲示する。
install.packages("MBESS", repos="https://cran.ism.ac.jp")
library("MBESS")
library("MBESS")

…(中略)…

…(中略)…

m0 <- by(data01$fincome, data01$sex, mean, na.rm=T)
v0 <- by(data01$fincome, data01$sex, var, na.rm=T)
n0 <- by(data01$fincome, data01$sex, function(x) sum(!is.na(x)))
m0
sd0 <- sqrt(sum(v0*(n0-1))/sum(n0-1)) # 平均的な標準偏差
es0 <- diff(rev(m0))/sd0; es0 # 標本効果サイズ
t0 <- es0 / sqrt(sum(1/n0)) # t統計量
lambda <- conf.limits.nct(t.value = t0, df=(sum(n0)-2), conf.level=.95, alpha.lower=NULL, alpha.upper=NULL)
lambda # 非心パラメタの下限と上限
# 非心パラメタの上限と下限を効果サイズに換算する
lambda$Lower.Limit * sqrt(sum(1/n0)); lambda$Upper.Limit * sqrt(sum(1/n0))
v0 <- by(data01$fincome, data01$sex, var, na.rm=T)
n0 <- by(data01$fincome, data01$sex, function(x) sum(!is.na(x)))
m0
sd0 <- sqrt(sum(v0*(n0-1))/sum(n0-1)) # 平均的な標準偏差
es0 <- diff(rev(m0))/sd0; es0 # 標本効果サイズ
t0 <- es0 / sqrt(sum(1/n0)) # t統計量
lambda <- conf.limits.nct(t.value = t0, df=(sum(n0)-2), conf.level=.95, alpha.lower=NULL, alpha.upper=NULL)
lambda # 非心パラメタの下限と上限
# 非心パラメタの上限と下限を効果サイズに換算する
lambda$Lower.Limit * sqrt(sum(1/n0)); lambda$Upper.Limit * sqrt(sum(1/n0))

発展1 正規性の検定(normality test)
まずはシャピロ・ウィルクの検定とコルモゴロフ・スミルノフ検定の実例を示そう。
注意すべき点は,shapiro.test( )は変数が欠損値NAを含んでいても実行可能であるが,ks.test( )はNAを許容しないことである。

男女別の幸福度と世帯年収の正規性の検定は以下で実行できる。結果は省略するが,全て5%水準で有意となり,「母集団において正規分布している」とのゼロ仮説が棄却されてしまう。
ヒストグラムとQ-Qプロットで視覚的に正規性を判断するスクリプトを紹介しよう。本文の男性の幸福度のグラフの最低限のものは以下で描ける。par (mfrow=c(1, 2))は,描画領域を1行2列に分割するというコマンドである。例示したグラフではまず右側にhist(v1, freq=F)でヒストグラムを描き,そこにcurve(dnorm(x, mean=mean(v1), sd=sd(v1)), from=0, to=10 , add=T)で正規分布を重ね描きしている。次に左側にqqnorm(v1)でQ-Qプロットを描き,qqline(v1)によって第1四分位と第3四分位を結んだ直線を重ねて描いている。
女性の幸福度に例を変えて,もう少し装飾を施したグラフを描いてみよう。
注意すべき点は,shapiro.test( )は変数が欠損値NAを含んでいても実行可能であるが,ks.test( )はNAを許容しないことである。
v1 <- data01$q1700b[data01$sex==1] # 欠損値含む
shapiro.test(v1)
ks.test(v1,"pnorm",mean=mean(v1),sd=sd(v1))
v1 <- data01$q1700b[data01$sex==1 & !is.na(data01$q1700b)] # 欠損値除外
ks.test(v1,"pnorm",mean=mean(v1),sd=sd(v1))
shapiro.test(v1)
ks.test(v1,"pnorm",mean=mean(v1),sd=sd(v1))
v1 <- data01$q1700b[data01$sex==1 & !is.na(data01$q1700b)] # 欠損値除外
ks.test(v1,"pnorm",mean=mean(v1),sd=sd(v1))

男女別の幸福度と世帯年収の正規性の検定は以下で実行できる。結果は省略するが,全て5%水準で有意となり,「母集団において正規分布している」とのゼロ仮説が棄却されてしまう。
v1 <- data01$q1700b[data01$sex==1 & !is.na(data01$q1700b)]
shapiro.test(v1)
ks.test(v1,"pnorm",mean=mean(v1),sd=sd(v1))
v1 <- data01$q1700b[data01$sex==2 & !is.na(data01$q1700b)]
shapiro.test(v1)
ks.test(v1,"pnorm",mean=mean(v1),sd=sd(v1))
v1 <- data01$fincome[data01$sex==1 & !is.na(data01$fincome)]
shapiro.test(v1)
ks.test(v1,"pnorm",mean=mean(v1),sd=sd(v1))
v1 <- data01$fincome[data01$sex==2 & !is.na(data01$fincome)]
shapiro.test(v1)
ks.test(v1,"pnorm",mean=mean(v1),sd=sd(v1))
shapiro.test(v1)
ks.test(v1,"pnorm",mean=mean(v1),sd=sd(v1))
v1 <- data01$q1700b[data01$sex==2 & !is.na(data01$q1700b)]
shapiro.test(v1)
ks.test(v1,"pnorm",mean=mean(v1),sd=sd(v1))
v1 <- data01$fincome[data01$sex==1 & !is.na(data01$fincome)]
shapiro.test(v1)
ks.test(v1,"pnorm",mean=mean(v1),sd=sd(v1))
v1 <- data01$fincome[data01$sex==2 & !is.na(data01$fincome)]
shapiro.test(v1)
ks.test(v1,"pnorm",mean=mean(v1),sd=sd(v1))
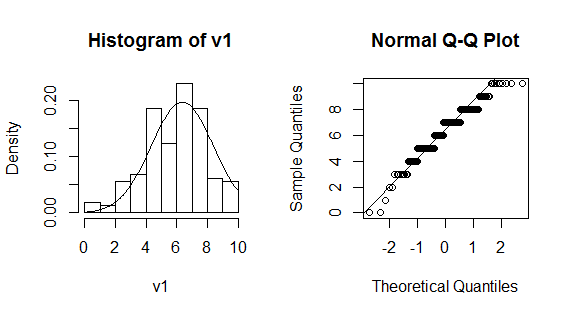
ヒストグラムとQ-Qプロットで視覚的に正規性を判断するスクリプトを紹介しよう。本文の男性の幸福度のグラフの最低限のものは以下で描ける。par (mfrow=c(1, 2))は,描画領域を1行2列に分割するというコマンドである。例示したグラフではまず右側にhist(v1, freq=F)でヒストグラムを描き,そこにcurve(dnorm(x, mean=mean(v1), sd=sd(v1)), from=0, to=10 , add=T)で正規分布を重ね描きしている。次に左側にqqnorm(v1)でQ-Qプロットを描き,qqline(v1)によって第1四分位と第3四分位を結んだ直線を重ねて描いている。
v1 <- data01$q1700b[data01$sex==1 & !is.na(data01$q1700b)]
par(mfrow=c(1,2))
hist(v1, freq=F)
curve(dnorm(x, mean=mean(v1), sd=sd(v1)), from=0, to=10 , add=T)
qqnorm(v1); qqline(v1)
par(mfrow=c(1,2))
hist(v1, freq=F)
curve(dnorm(x, mean=mean(v1), sd=sd(v1)), from=0, to=10 , add=T)
qqnorm(v1); qqline(v1)

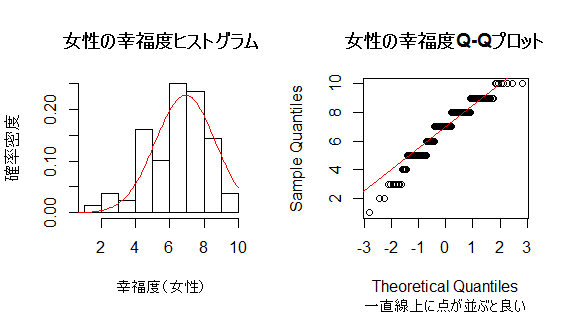
女性の幸福度に例を変えて,もう少し装飾を施したグラフを描いてみよう。
v1 <- data01$q1700b[data01$sex==2 & !is.na(data01$q1700b)]
par(mfrow=c(1,2))
hist(v1, main="女性の幸福度ヒストグラム", xlab="幸福度(女性)", ylab="確率密度", freq=F)
curve(dnorm(x, mean=mean(v1), sd=sd(v1)), from=0, to=10 , add=T, col="red")
qqnorm(v1, main="女性の幸福度Q-Qプロット", sub="一直線上に点が並ぶと良い")
qqline(v1, col="red")
par(mfrow=c(1,2))
hist(v1, main="女性の幸福度ヒストグラム", xlab="幸福度(女性)", ylab="確率密度", freq=F)
curve(dnorm(x, mean=mean(v1), sd=sd(v1)), from=0, to=10 , add=T, col="red")
qqnorm(v1, main="女性の幸福度Q-Qプロット", sub="一直線上に点が並ぶと良い")
qqline(v1, col="red")

第6章の【練習問題】の解答
1) の答え: スクリプトと結果を以下に示す。
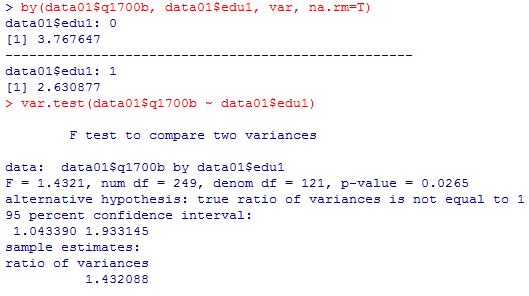

2) の答え: 平均値差は,大卒の幸福度−非大卒の幸福度 で計算する。

3) の答え: 用いる標準偏差は3通りとする。検定力は30%以下であり,高くない。そもそも1)の検定で有意にならない程度の平均値差なのであるから,もしもそれを検出しようとするなら大きなサンプルサイズが必要である。

4) の答え: スクリプトは本文にあるので,ここでは指示に従って何度か繰り返したうちの2回分の結果を示す。母数の設定で明らかな様に,本当は母平均には差があるが,母標準偏差にもかなりの差がある。ケース数も異なる。この条件で,「母平均には差がない」と云うゼロ仮説を正しく棄却出来るか否かに関心がある。
【実行例?】辛うじていずれもゼロ仮説を5%水準で棄却する。

【実行例?】Studentのt検定はゼロ仮説を棄却出来ない。

5) の答え: ここではmu2は変えずに。n2とsd2を変えて検定結果がどの様に変わるかを示す。
【実行例?】n2のサンプルサイズを半分にすると,ゼロ仮説を棄却出来ない事が多くなる。

【実行例?】更にバラツキsd2を半分にすると,ゼロ仮説がかなり棄却出来る様になる。

同じ条件で何度も繰り返し実行してみると(シミュレイション),条件が同じであるにも関わらずかなり変動が大きい事が分かるだろう。これはサンプルサイズが比較的小さく設定してある事にもよる。逆に両方のサンプルサイズが大きければ,母平均の差がもっと小さくてもゼロ仮説をよく棄却する(大標本による検定は検定力が高い=感受性が高い)。試してみると良い。
data01$q1700b <- c(0:10)[data01$q1700+1] # 欠損値処理
by(data01$q1700b, data01$edu1, var, na.rm=T)
var.test(data01$q1700b ~ data01$edu1)
t.test(data01$q1700b ~ data01$edu1)
t.test(data01$q1700b ~ data01$edu1, var.equal=T)
by(data01$q1700b, data01$edu1, var, na.rm=T)
var.test(data01$q1700b ~ data01$edu1)
t.test(data01$q1700b ~ data01$edu1)
t.test(data01$q1700b ~ data01$edu1, var.equal=T)


2) の答え: 平均値差は,大卒の幸福度−非大卒の幸福度 で計算する。
m0 <- by(data01$q1700b, data01$edu1, mean, na.rm=T); m0
v0 <- by(data01$q1700b, data01$edu1, var, na.rm=T)
n0 <- by(data01$q1700b, data01$edu1, function(x) sum(!is.na(x))); n0
m_diff <- diff(m0); m_diff # 学歴別の幸福度の標本平均差
sigma <- sqrt(sum(v0*(n0 - 1))/(sum(n0)-2)) # 共通の母標準偏差の推定値
sd0 <- c(sqrt(v0), sigma); sd0
es <- m_diff/sd0; es # 標本効果サイズ
v0 <- by(data01$q1700b, data01$edu1, var, na.rm=T)
n0 <- by(data01$q1700b, data01$edu1, function(x) sum(!is.na(x))); n0
m_diff <- diff(m0); m_diff # 学歴別の幸福度の標本平均差
sigma <- sqrt(sum(v0*(n0 - 1))/(sum(n0)-2)) # 共通の母標準偏差の推定値
sd0 <- c(sqrt(v0), sigma); sd0
es <- m_diff/sd0; es # 標本効果サイズ

3) の答え: 用いる標準偏差は3通りとする。検定力は30%以下であり,高くない。そもそも1)の検定で有意にならない程度の平均値差なのであるから,もしもそれを検出しようとするなら大きなサンプルサイズが必要である。
m0 <- by(data01$q1700b, data01$edu1, mean, na.rm=T); m0
v0 <- by(data01$q1700b, data01$edu1, var, na.rm=T)
n0 <- by(data01$q1700b, data01$edu1, function(x) sum(!is.na(x))); n0
m_diff <- diff(m0); m_diff # 学歴別の幸福度の標本平均差
sigma <- sqrt(sum(v0*(n0 - 1))/(sum(n0)-2)) # 共通の母標準偏差の推定値
sd0 <- c(sqrt(v0), sigma); sd0
es <- m_diff/sd0; es # 標本効果サイズ
pwr.t2n.test(n0[1], n0[2], d=es, sig.level=.05, power=NULL, alternative="two.sided")
v0 <- by(data01$q1700b, data01$edu1, var, na.rm=T)
n0 <- by(data01$q1700b, data01$edu1, function(x) sum(!is.na(x))); n0
m_diff <- diff(m0); m_diff # 学歴別の幸福度の標本平均差
sigma <- sqrt(sum(v0*(n0 - 1))/(sum(n0)-2)) # 共通の母標準偏差の推定値
sd0 <- c(sqrt(v0), sigma); sd0
es <- m_diff/sd0; es # 標本効果サイズ
pwr.t2n.test(n0[1], n0[2], d=es, sig.level=.05, power=NULL, alternative="two.sided")

4) の答え: スクリプトは本文にあるので,ここでは指示に従って何度か繰り返したうちの2回分の結果を示す。母数の設定で明らかな様に,本当は母平均には差があるが,母標準偏差にもかなりの差がある。ケース数も異なる。この条件で,「母平均には差がない」と云うゼロ仮説を正しく棄却出来るか否かに関心がある。
【実行例?】辛うじていずれもゼロ仮説を5%水準で棄却する。

【実行例?】Studentのt検定はゼロ仮説を棄却出来ない。

5) の答え: ここではmu2は変えずに。n2とsd2を変えて検定結果がどの様に変わるかを示す。
【実行例?】n2のサンプルサイズを半分にすると,ゼロ仮説を棄却出来ない事が多くなる。

【実行例?】更にバラツキsd2を半分にすると,ゼロ仮説がかなり棄却出来る様になる。

同じ条件で何度も繰り返し実行してみると(シミュレイション),条件が同じであるにも関わらずかなり変動が大きい事が分かるだろう。これはサンプルサイズが比較的小さく設定してある事にもよる。逆に両方のサンプルサイズが大きければ,母平均の差がもっと小さくてもゼロ仮説をよく棄却する(大標本による検定は検定力が高い=感受性が高い)。試してみると良い。
ウェブ増補1 対応のある2群の母平均の差の検定
第6章で解説したのは,「対応のない2群の母平均の差の検定」と呼ばれるものである。紙幅の都合上テクストでは割愛したが,2群の母平均の差の検定には,「対応のある2群」のものもある。ここで一応説明しておこう。
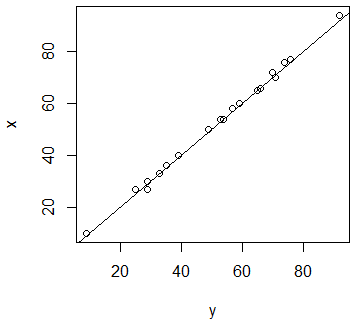
まずはこの2変数xとyをそれぞれ別々に(あたかも対応が無いかの様に)要約し,箱ひげ図を描いてみよう。
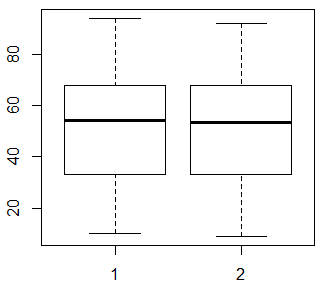

箱ひげ図を見ても,x(1)とy(2)は殆ど同じ分布であり,要約統計量に見られる違いも僅かである。スチューデントのt検定とウェルチの検定の両方の結果を示しておいたがいずれにしても殆ど違わず(xとyがほぼ等分散である為),標本平均の小さな差は,統計的に全く有意にならない。つまり,「xとyの母平均は等しい」と云うゼロ仮説を棄却する証拠は全然得られなかったと云う結果になる。
但し確認しておきたいのは,変数の作成の仕方や散布図からは,明らかにxはyより大きい傾向がある筈なのである。
xとyはそもそも関係がある。こうした場合を「対応のある場合」と呼ぶ。実験データや社会調査データで言えば,同一個人から2回測定した場合,同一個人に二つの質問をした場合がその典型である。二つの変数を比較するのだが,一方の変数が明らかに他方の変数に基づいているか(実験における事前―事後の測定),或は同じ個人の性格や属性から2変数とも共通の影響を受けていると云った場合は,「対応のある場合」の検定を行うべきである。
そうした場合は,各ケース(各ユニット)について,xとyの値の差を求めて,個人個人について計算されるその差について検討する。対応のない場合の母平均の差の検定は,2つの平均を求めてからその差について検討したが,対応のある場合の母平均の差の検定は,まず個々に差を求めてからその平均について検討するのである。
よって以下ではまず,xとyの差x-yの要約統計量を求めて箱ひげ図を描く。これによって明らかにxはyよりも大きい傾向がある事が確認される。そしてその差についてt検定を行う。関数は t.test( ) であり,これにオプションの paired=TRUE を付けるだけで良い。

検定結果は,1%水準で有意となり,平均における真の差(母平均差)は0ではないとの対抗仮説が採択される。差の95%信頼区間も求められているが,検定結果と平仄があっており,区間に0は含んでいない。本来僅かな差がある筈のデータについて,変数値に関連があると云う情報を考慮する事によって,その差を確かに検出する事が出来る様になったのである。
上の検定は,「対応のある2群の母平均の差が0である」=「値の差x-yの平均が0である」と云うゼロ仮説を設定し,そこからのズレが偶然の範囲内と言えるかどうかを検討している。要するに,「或1つの変数(x-y)の母平均が0である」と云うゼロ仮説を検定しているだけなので,単純な「母平均の検定」に帰着する。ケース数はn,標準偏差はsd(x-y)で求められるので,標本平均の標準誤差(の推定値)は sd(x-y)/sqrt(n) となり,ここから検定統計量t=mean(x-y)/(sd(x-y)/sqrt(n))が自由度n-1のt分布に近似的に従う事が言え,t統計量の値,それに対応する有意確率を求める事が出来る。以下がそのスクリプトで,95%信頼区間も求めている。

先の"Paired t-test"の結果と見比べると,mean of the differences と mean(x-y)の値は0.7で一致し,t統計量の値(約3.0361),有意確率(約0.006796)も一致している。95%信頼区間の上限と下限も一致している事が確認出来る。「対応のある二群の母平均の差の検定」は,「引き算した値の母平均が0でないと言えるかどうか」を検定しているに過ぎない事がこれで確認出来た。
対応のある2群の母平均の差の検定
以下のシミュレイションでは,まずサイズnの正規変量を整数化した変数xを生成し,そのxから平均1・分散1の正規変量を減じて整数化した変数yを生成する。一言で言えば,xとyはほぼ同じくらいの値であるが,yの方がやや小さくなる傾向がある。その事を,cor( ),plot( )で確認する。グラフから,yはxとほぼ同じ値であるが,xより僅かに小さい場合が多い事が確認出来る。
#### 対応のある二群の母平均の差の検定 ####
# 意図的に,xがyよりも僅かに大きくなる傾向のある2変数を作成する
n <- 20
x <- round(rnorm(n, mean=50, sd=20), 0)
y <- round(x - rnorm(n, mean=1, sd=1), 0)
cor(y, x); plot(y, x); abline(0, 1)
# 意図的に,xがyよりも僅かに大きくなる傾向のある2変数を作成する
n <- 20
x <- round(rnorm(n, mean=50, sd=20), 0)
y <- round(x - rnorm(n, mean=1, sd=1), 0)
cor(y, x); plot(y, x); abline(0, 1)
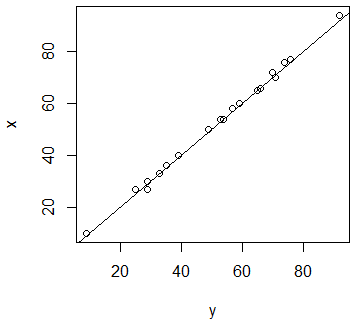
まずはこの2変数xとyをそれぞれ別々に(あたかも対応が無いかの様に)要約し,箱ひげ図を描いてみよう。
summary(cbind(x, y)); boxplot(x, y) # それぞれの変数の個別の要約
t.test(x, y, var.equal=T) # 対応のない母平均差のスチューデントのt検定
t.test(x, y) # 対応のない母平均差のウェルチのt検定
t.test(x, y, var.equal=T) # 対応のない母平均差のスチューデントのt検定
t.test(x, y) # 対応のない母平均差のウェルチのt検定


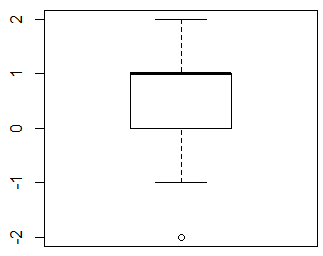
箱ひげ図を見ても,x(1)とy(2)は殆ど同じ分布であり,要約統計量に見られる違いも僅かである。スチューデントのt検定とウェルチの検定の両方の結果を示しておいたがいずれにしても殆ど違わず(xとyがほぼ等分散である為),標本平均の小さな差は,統計的に全く有意にならない。つまり,「xとyの母平均は等しい」と云うゼロ仮説を棄却する証拠は全然得られなかったと云う結果になる。
但し確認しておきたいのは,変数の作成の仕方や散布図からは,明らかにxはyより大きい傾向がある筈なのである。
xとyはそもそも関係がある。こうした場合を「対応のある場合」と呼ぶ。実験データや社会調査データで言えば,同一個人から2回測定した場合,同一個人に二つの質問をした場合がその典型である。二つの変数を比較するのだが,一方の変数が明らかに他方の変数に基づいているか(実験における事前―事後の測定),或は同じ個人の性格や属性から2変数とも共通の影響を受けていると云った場合は,「対応のある場合」の検定を行うべきである。
そうした場合は,各ケース(各ユニット)について,xとyの値の差を求めて,個人個人について計算されるその差について検討する。対応のない場合の母平均の差の検定は,2つの平均を求めてからその差について検討したが,対応のある場合の母平均の差の検定は,まず個々に差を求めてからその平均について検討するのである。
よって以下ではまず,xとyの差x-yの要約統計量を求めて箱ひげ図を描く。これによって明らかにxはyよりも大きい傾向がある事が確認される。そしてその差についてt検定を行う。関数は t.test( ) であり,これにオプションの paired=TRUE を付けるだけで良い。
summary(x-y); boxplot(x-y) # 変数値の差の要約
t.test(x, y, paired=T) # 対応のある母平均差の検定
t.test(x, y, paired=T) # 対応のある母平均差の検定


検定結果は,1%水準で有意となり,平均における真の差(母平均差)は0ではないとの対抗仮説が採択される。差の95%信頼区間も求められているが,検定結果と平仄があっており,区間に0は含んでいない。本来僅かな差がある筈のデータについて,変数値に関連があると云う情報を考慮する事によって,その差を確かに検出する事が出来る様になったのである。
半分は自力でこの検定結果を再現する
上では,t.test( )関数にpaired=Tオプションを指定するだけで済んだので簡単に実行出来たが,その分,何を計算しているのかなどは分からなくなってしまっている。よって以下で,上の t.test(x, y, paired=T) の結果を再現し,それを通して理解を深める事を目指す。上の検定は,「対応のある2群の母平均の差が0である」=「値の差x-yの平均が0である」と云うゼロ仮説を設定し,そこからのズレが偶然の範囲内と言えるかどうかを検討している。要するに,「或1つの変数(x-y)の母平均が0である」と云うゼロ仮説を検定しているだけなので,単純な「母平均の検定」に帰着する。ケース数はn,標準偏差はsd(x-y)で求められるので,標本平均の標準誤差(の推定値)は sd(x-y)/sqrt(n) となり,ここから検定統計量t=mean(x-y)/(sd(x-y)/sqrt(n))が自由度n-1のt分布に近似的に従う事が言え,t統計量の値,それに対応する有意確率を求める事が出来る。以下がそのスクリプトで,95%信頼区間も求めている。
# 対応のある二群の母平均の差のt検定: マニュアル
mean(x-y) # 差の平均
t0 <- mean(x-y)/(sd(x-y)/sqrt(n)); t0 # t統計量
2*(1-pt(abs(t0), df=n-1)) # 両側有意確率
# 95%信頼区間
mean(x-y)-qt(.975, df=n-1)*sd(x-y)/sqrt(n)
mean(x-y)+qt(.975, df=n-1)*sd(x-y)/sqrt(n)
mean(x-y) # 差の平均
t0 <- mean(x-y)/(sd(x-y)/sqrt(n)); t0 # t統計量
2*(1-pt(abs(t0), df=n-1)) # 両側有意確率
# 95%信頼区間
mean(x-y)-qt(.975, df=n-1)*sd(x-y)/sqrt(n)
mean(x-y)+qt(.975, df=n-1)*sd(x-y)/sqrt(n)

先の"Paired t-test"の結果と見比べると,mean of the differences と mean(x-y)の値は0.7で一致し,t統計量の値(約3.0361),有意確率(約0.006796)も一致している。95%信頼区間の上限と下限も一致している事が確認出来る。「対応のある二群の母平均の差の検定」は,「引き算した値の母平均が0でないと言えるかどうか」を検定しているに過ぎない事がこれで確認出来た。
ウェブ増補2 対応のない2群の母比率の差の検定
比率については,第3章の発展1で母比率の区間推定を紹介したのみだが,母平均の場合と同じ様に,二つの母比率に差があると言えるかどうかの検定も存在しており,やはり「対応のない場合」と「対応のある場合」に分けられる。この項目ではまず「対応のない場合」を説明する。
関東での標本比率を.150,関西での標本視聴率を.130だったとしよう。以上の情報で,prop.test( )関数を用いて,ゼロ仮説の有意性検定を実行する事が出来る。この関数はデフォルトでは第5章発展1-2のイェーツの連続性修正同様の修正を行うので,それを行わない場合と行う(デフォルトの)場合の両方を示しておく。

またしても,自動で検定してくれるのは便利ではあるが,正直何をどうしたのかは分からない。結果から,カイ二乗検定を行っているらしいと云う事は読み取れるが,その値がどの様に計算されたのかは分からない。因みに,上の結果はいずれも,関東と関西の母視聴率に差があるとは言えないと云う検定結果を示している。900世帯の標本比率15%と600世帯の標本比率13%では,母集団でも関東の方が視聴率が良かったと結論するには不十分なのである。比率の差の95%信頼区間も求められているが,0を挟んでマイナスからプラスの領域に広がっており,「関西の方が高いかも知れないし,関東の方が高いかも知れない」と云う結果を意味しているのである。
第5章発展1-2で説明した通り,分割表の独立性のカイ二乗検定を行う代わりに,より正確なフィッシャーの正確検定(直接確率)を用いる事も出来る。

ゼロ仮説が正しければそれぞれの母集団での視聴率は等しいと仮定されるので,その共通の母比率の推定値Pを,標本比率の加重平均として求める。そうすると母分散の推定値はP(1-P)となり,標本平均の一種とも言える標本比率の差の検定は,第6章基礎1-2のt統計量の計算と同様にして検定統計量を求める事が出来る。そこからするとこの検定統計量はt分布に従うと考えるべきであるが,比率の場合は母分散が小数になり,標本分散による母分散の過小推定の問題も小さいからか,標準正規分布に従うと考えて検定を行う。
検定統計量が標準正規変量と見做せるならば,その二乗は,確率分布の定義から,自由度1のカイ二乗分布に従う事になる。よってカイ二乗分布を用いて検定を行っても全く同じである。これらをRで実行してみる。後半は連続性修正を行う方法を定義に従って実行している。

標準正規分布を用いた検定結果とカイ二乗分布を用いた検定結果は,有意確率が完全に一致しており,同じ事を行っているのだと云う事が納得出来るであろう。前半のt分布を用いた場合も有意確率の相違は極めて僅かである。
prop.test( )の結果と見比べても,カイ二乗値や有意確率が一致している事が確認出来る。つまり,先のprop.test( )のカイ二乗検定は,母比率の差のz検定と等価であると言える。そして母比率の差のz検定は,母平均の差のt検定と同じ公式から求められるのである。対応のない二群の母比率の差の検定は,比率が0-1変数の平均である事に着目して,対応のない二群の母平均の差の検定を適用しても近似的に実行出来るのである。
2行×2列の分割表に表現して独立性の検定を行った結果とも完全に一致している。検定するだけであれば分割表のカイ二乗検定が一番簡単にも思えるが,比率の差の区間推定を行いたい場合には,porp.test( )を用いるか,自分でz統計量を求めて信頼区間を求める事が必要になる。
この様に,実質的には同じ事を検定する為に,一見色々と異なった方法が存在する事がある。それぞれがどの様に関係しているか,どの様に一致するかをこうしてきちんと確認してゆくと,単に公式を機械的に当てはめるのではなく,また検定や推定の中身をブラックボックス化させずに理解を深める事が出来るだろう。
対応のない2群の母比率の差のカイ二乗検定
例として,或TV番組についての,関東地区の世帯視聴率と関西地区の世帯視聴率を考えてみよう。調査世帯数は関東では900世帯,関西では600世帯であり,全く異なる別々の二つの集団から二値変数(0か1の値)を収集してその平均(つまり1の値を取る世帯の比率)を求めており,それぞれの個々の測定値には何の対応も関係も無い。検定の為のゼロ仮説は「関東の母比率と関西の母比率は等しい」である。関東での標本比率を.150,関西での標本視聴率を.130だったとしよう。以上の情報で,prop.test( )関数を用いて,ゼロ仮説の有意性検定を実行する事が出来る。この関数はデフォルトでは第5章発展1-2のイェーツの連続性修正同様の修正を行うので,それを行わない場合と行う(デフォルトの)場合の両方を示しておく。
# 対応のない母比率の差の検定。関東(E)と関西(W)での視聴率
nE <- 900
nW <- 600
pE <- .150 # 計算の都合上小数第3位は0とする。
pW <- .130
prop.test(c(nE*pE, nW*pW), c(nE, nW), correct=F)
prop.test(c(nE*pE, nW*pW), c(nE, nW)) # デフォルトでは連続性修正
nE <- 900
nW <- 600
pE <- .150 # 計算の都合上小数第3位は0とする。
pW <- .130
prop.test(c(nE*pE, nW*pW), c(nE, nW), correct=F)
prop.test(c(nE*pE, nW*pW), c(nE, nW)) # デフォルトでは連続性修正

またしても,自動で検定してくれるのは便利ではあるが,正直何をどうしたのかは分からない。結果から,カイ二乗検定を行っているらしいと云う事は読み取れるが,その値がどの様に計算されたのかは分からない。因みに,上の結果はいずれも,関東と関西の母視聴率に差があるとは言えないと云う検定結果を示している。900世帯の標本比率15%と600世帯の標本比率13%では,母集団でも関東の方が視聴率が良かったと結論するには不十分なのである。比率の差の95%信頼区間も求められているが,0を挟んでマイナスからプラスの領域に広がっており,「関西の方が高いかも知れないし,関東の方が高いかも知れない」と云う結果を意味しているのである。
分割表を用いた比率の差のカイ二乗検定
カイ二乗検定を用いているのだから,すぐに思いつくのは分割表(クロス表)の独立性の検定である。一方の変数は地域(関東と関西),他方の変数は視聴の有無なので,2行×2列の分割表で表現する事が出来,2変数に関連が無いかどうか(つまり2つの地域で比が等しいか否か)を検定する事が出来る筈である。以下のスクリプトはそれを実行するものであり,結果を上のprop.test( )と見比べると,連続性の修正をする場合としない場合でそれぞれ全く一致している事が分かる。第5章発展1-2で説明した通り,分割表の独立性のカイ二乗検定を行う代わりに,より正確なフィッシャーの正確検定(直接確率)を用いる事も出来る。
# 分割表を用いたカイ二乗検定
x1 <- matrix(c(nE*pE, nW*pW, nE*(1-pE), nW*(1-pW)), ncol=2); x1
chisq.test(x1, correct=F) # イェーツの連続性修正無し
chisq.test(x1) # イェーツの連続性修正有り
fisher.test(x1) # どうせなら正確検定
x1 <- matrix(c(nE*pE, nW*pW, nE*(1-pE), nW*(1-pW)), ncol=2); x1
chisq.test(x1, correct=F) # イェーツの連続性修正無し
chisq.test(x1) # イェーツの連続性修正有り
fisher.test(x1) # どうせなら正確検定

対応のない2群の母比率の差のz検定
分割表で検定出来てしまうのでこれ以上追究する意味も余り無いと感じられるが,他によく紹介される方法にも触れておく。ゼロ仮説が正しければそれぞれの母集団での視聴率は等しいと仮定されるので,その共通の母比率の推定値Pを,標本比率の加重平均として求める。そうすると母分散の推定値はP(1-P)となり,標本平均の一種とも言える標本比率の差の検定は,第6章基礎1-2のt統計量の計算と同様にして検定統計量を求める事が出来る。そこからするとこの検定統計量はt分布に従うと考えるべきであるが,比率の場合は母分散が小数になり,標本分散による母分散の過小推定の問題も小さいからか,標準正規分布に従うと考えて検定を行う。
検定統計量が標準正規変量と見做せるならば,その二乗は,確率分布の定義から,自由度1のカイ二乗分布に従う事になる。よってカイ二乗分布を用いて検定を行っても全く同じである。これらをRで実行してみる。後半は連続性修正を行う方法を定義に従って実行している。
# 母比率は等しいとのゼロ仮説の下での,共通の母比率推定値P
P <- (nE*pE+nW*pW)/(nE+nW)
z <- abs(pE-pW)/sqrt(P*(1-P)*(1/nE+1/nW)); z # 標準正規変量
2*(1-pnorm(z, 0, 1)) # 標準正規分布を用いた両側有意確率
2*(1-pt(z, df=nE+nW-2)) # t分布を用いた両側有意確率
z^2 # 自由度1のカイ二乗統計量
1-pchisq(z^2, df=1) # カイ二乗分布を用いた有意確率
# 比率の差の場合の連続性修正の公式
zc <- (abs(pE-pW)-.5*(1/nE+1/nW))/sqrt(P*(1-P)*(1/nE+1/nW)); zc # 標準正規変量
2*(1-pnorm(zc, 0, 1)) # 標準正規分布を用いた両側有意確率
zc^2 # 自由度1のカイ二乗統計量
1-pchisq(zc^2, df=1) # カイ二乗分布を用いた有意確率
P <- (nE*pE+nW*pW)/(nE+nW)
z <- abs(pE-pW)/sqrt(P*(1-P)*(1/nE+1/nW)); z # 標準正規変量
2*(1-pnorm(z, 0, 1)) # 標準正規分布を用いた両側有意確率
2*(1-pt(z, df=nE+nW-2)) # t分布を用いた両側有意確率
z^2 # 自由度1のカイ二乗統計量
1-pchisq(z^2, df=1) # カイ二乗分布を用いた有意確率
# 比率の差の場合の連続性修正の公式
zc <- (abs(pE-pW)-.5*(1/nE+1/nW))/sqrt(P*(1-P)*(1/nE+1/nW)); zc # 標準正規変量
2*(1-pnorm(zc, 0, 1)) # 標準正規分布を用いた両側有意確率
zc^2 # 自由度1のカイ二乗統計量
1-pchisq(zc^2, df=1) # カイ二乗分布を用いた有意確率

標準正規分布を用いた検定結果とカイ二乗分布を用いた検定結果は,有意確率が完全に一致しており,同じ事を行っているのだと云う事が納得出来るであろう。前半のt分布を用いた場合も有意確率の相違は極めて僅かである。
prop.test( )の結果と見比べても,カイ二乗値や有意確率が一致している事が確認出来る。つまり,先のprop.test( )のカイ二乗検定は,母比率の差のz検定と等価であると言える。そして母比率の差のz検定は,母平均の差のt検定と同じ公式から求められるのである。対応のない二群の母比率の差の検定は,比率が0-1変数の平均である事に着目して,対応のない二群の母平均の差の検定を適用しても近似的に実行出来るのである。
2行×2列の分割表に表現して独立性の検定を行った結果とも完全に一致している。検定するだけであれば分割表のカイ二乗検定が一番簡単にも思えるが,比率の差の区間推定を行いたい場合には,porp.test( )を用いるか,自分でz統計量を求めて信頼区間を求める事が必要になる。
この様に,実質的には同じ事を検定する為に,一見色々と異なった方法が存在する事がある。それぞれがどの様に関係しているか,どの様に一致するかをこうしてきちんと確認してゆくと,単に公式を機械的に当てはめるのではなく,また検定や推定の中身をブラックボックス化させずに理解を深める事が出来るだろう。
ウェブ増補3 対応のある2群の母比率の差の検定
対応のある2群と云うのはウェブ増補1で書いた通り,同一個人から2回測定した場合,同一個人に2つの質問をした場合などを指す。世帯視聴率で言えば,同じ関東地区の900世帯で,異なるドラマの視聴率(比率)に差があると言えるかどうかは,対応のある場合となる。
対応のある2群の母比率の差の検定にも,3通りくらいの方法がある。一つは標準正規分布を用いた検定法,2つ目はマクネマー検定と呼ばれる有名な方法,3つ目は2項分布を用いた方法である。標準正規分布を用いる方法は標準誤差の計算が簡単には分からない。マクネマー検定は最もよく紹介されている様に思えるが,ユーザにとってはかなりブラックボックスな感覚になる。結局,2項分布を用いた方法が最もすっきりしているのではないかと思われる。
関東地区の900世帯で世帯視聴率調査を行って,同じ週に放映された二つのドラマの視聴率を比較したとしよう。一方のドラマ1は16.0%,他方のドラマ2は13.0%であった。これらの視聴率は標本比率である。母集団は関東地区の約1,835万世帯であるが,母集団における視聴率(母比率)もドラマ1の方が高かったと言えるだろうか。(視聴率調査最大手のビデオリサーチについては,週間高世帯視聴率番組10や視聴率調査について(視聴率ハンドブック)を参照の事。)
これがもし「対応のない2群」であれば,上の「ウェブ増補2」で紹介した様に,分割表にして独立性のカイ二乗検定を行えばよい。結果は各自でやってみて欲しいが,χ2(df=1)=3.34, 有意確率p=.06755で5%で有意にならない。つまり,ドラマ1の方が母集団での視聴率が高かったと云う証拠としては不十分である。
論理的には,900世帯は,ドラマ1も2も見た世帯,1か2の一方のみ見た世帯,いずれも見なかった世帯の4通りに分類される。ドラマ1を見た/見ていない,ドラマ2を見た/見ていないの2行×2列の分割表で表現される筈である。これが対応のある場合の比率の差を考える出発点である。
しかし,視聴率調査では,そこまで詳しい情報は一般には公開されていないので,我々にはこの分割表は作る事が出来ない。
そこで以下では,3つの対照的な分割表xa, xb, xcについて分析して比較しよう。参考までにそのままカイ二乗検定を行った結果(2行2列なのでデフォルトでイェーツの連続性修正付き)も添えているが,これは「ドラマ1の視聴とドラマ2の視聴は全く関連が無い」と云うゼロ仮説の検定であり,母比率に差があると言えるかどうかの検定とは全く別物である事に注意して欲しい。
3つの分割表は全て周辺度数は(当然)同一であるが,分割表の中身は大きく異なる。


対応のある2群の母比率の検定では,「ドラマ1もドラマ2も見た」人達,「両方とも見なかった」人達は考慮に入れない。この人達は母比率に差をもたらす事が定義上無いからである。注目されるのは,「ドラマ1は見たがドラマ2は見なかった」人達(1行2列)と「ドラマ1は見なかったがドラマ2は見た」人達(2行1列)だけである。例えば分割表xaでは1行2列は27人,2行1列は0人,合計で27人であるが,「この人達は本来,いずれのセルに入るかは五分五分であり,この標本ではたまたま1行2列に27人が入った」と云う確率が小さいか,そうでないかを検定する。分割表xbでは125人と98人で合計223人,分割表xcでは144人と117人で合計261人が対象である。
標準正規分布による検定では,1行2列(または2行1列でも良い)に入る人数は本来はn1+n2-2*a11の半分であるが(=期待値),それが偶然にn1-a11になったと云う確率が小さいか否かを考える。この人数の標準誤差はsqrt((n1+n2-2*a11)*.5*(1-.5))となる事が分かっているので(2項分布の平均と分散),確率的に変動する「1行2列の人数」を標準化すると((n2-n11)-.5*(n1+n2-2*n11))/sqrt((n1+n2-2*n11)*.5*.5)となる。これが標準正規分布に従う事を利用して検定を行う。
以下に3つの場合全てについてこの標準正規分布検定を示した。後でマクネマー検定との関係を示す為に,標準正規変量を二乗した値(自由度1のカイ二乗変量になる)も示してある。

本来半々の筈が27対0になる事はおよそ偶然とは考えられないが,偶然に125対98(約1.28倍)や144対117(約1.23倍)になる事は20回に1回よりは多く起こり得るのでそれ程おかしくはないと云う結果になっている。


これも自動的に検定を行ってくれるのでとても便利であるが,カイ二乗検定である事以外はここからはよく分からない。
ただ,先の標準正規分布による検定のp値及びカイ二乗値(標準正規変量の二乗)と(修正なしの)マクネマー検定の結果を見比べると,3つとも一致している事が確認出来る。マクネマー検定の方は連続性の修正を行う事は出来るが,基本的には同じ様な事をしているのだと理解する事が出来る(検定結果については最後に纏める)。
であれば,最初から素直に2項検定を行うのが分かり易い。Rには2項検定を簡単に実行する binom.test( )関数がある。


number of trials が問題の2つのセルの度数合計,number of successes が1行2列の実際の度数,そこに当てはまる確率が.5である。 p-value がその2項検定の結果の有意確率である。やはりxaでは高度に有意,xb,xcでは5%で有意にならない。
最後のxcの場合を用いて,この2項検定をもう少し丁寧に確認してみよう。

多い方のセルの度数以上になるか,もしくは少ない方のセルの度数以下になる確率の合計が両側有意確率であり,これを pbinom( )関数で求めると,上の binom.test( )の結果に一致している。全部自動で実行してくれる関数はとても便利であるが,少なくとも最初は,それが何をやっているのかをこの様に確認しながら理解していく様にしよう。
最後に,以上の数種類の検定結果を簡単に纏めて比較しておく。
xaの様な極端な場合を除いて,xb,xcでは標準正規検定や連続性修正無しのマクネマー検定では2項検定よりも有意確率が低く,ゼロ仮説が棄却されやすい傾向が見られる。実際より有意確率が低くなると云う事は,第1種の過誤(αエラー)を犯しやすくなると云う事である。但し,この傾向は絶対ではなく,上の例でも,1行1列のセルの度数を色々と変えて行ってみると,p(マクネマー修正なし)>p(2項検定)となる場合も無い訳では無い(一方のセルの度数がかなり小さくて有意確率が極めて小さくなる条件下)。
連続性修正を行ったマクネマー検定は2項検定の結果にかなり近い。Rでは連続性修正を行うのがデフォルトでもあり,簡単に「対応のある2群の母比率の差の検定」を行う為に適してはいるが,2項検定も同じくらい簡単に実行出来るので,敢えてマクネマー検定を行う意味があるかどうかは不明である。
対応のある2群の母比率の差の検定にも,3通りくらいの方法がある。一つは標準正規分布を用いた検定法,2つ目はマクネマー検定と呼ばれる有名な方法,3つ目は2項分布を用いた方法である。標準正規分布を用いる方法は標準誤差の計算が簡単には分からない。マクネマー検定は最もよく紹介されている様に思えるが,ユーザにとってはかなりブラックボックスな感覚になる。結局,2項分布を用いた方法が最もすっきりしているのではないかと思われる。
関東地区の900世帯で世帯視聴率調査を行って,同じ週に放映された二つのドラマの視聴率を比較したとしよう。一方のドラマ1は16.0%,他方のドラマ2は13.0%であった。これらの視聴率は標本比率である。母集団は関東地区の約1,835万世帯であるが,母集団における視聴率(母比率)もドラマ1の方が高かったと言えるだろうか。(視聴率調査最大手のビデオリサーチについては,週間高世帯視聴率番組10や視聴率調査について(視聴率ハンドブック)を参照の事。)
これがもし「対応のない2群」であれば,上の「ウェブ増補2」で紹介した様に,分割表にして独立性のカイ二乗検定を行えばよい。結果は各自でやってみて欲しいが,χ2(df=1)=3.34, 有意確率p=.06755で5%で有意にならない。つまり,ドラマ1の方が母集団での視聴率が高かったと云う証拠としては不十分である。
# 二つのTV番組の視聴率の例
n <- 900
p1 <- .160 # 便宜上,視聴率は小数第二位までとしておく
p2 <- .130
n1 <- n*p1; n2 <- n*p2; n1; n2
# 「対応がない場合」で計算してみる
x0 <- matrix(c( n1, n2, n-n1, n-n2), ncol=2)
addmargins(x0)
chisq.test(x0)
ここで重要なのは,同じ900世帯に対して,二つのTV番組の視聴率を調べていると云う点であり,世帯数は全部で900である。上の様に対応の無い場合のカイ二乗検定を行うとあたかも全部で1800世帯あるかの様になってしまう(自分で上のスクリプトを実行して確認せよ)。n <- 900
p1 <- .160 # 便宜上,視聴率は小数第二位までとしておく
p2 <- .130
n1 <- n*p1; n2 <- n*p2; n1; n2
# 「対応がない場合」で計算してみる
x0 <- matrix(c( n1, n2, n-n1, n-n2), ncol=2)
addmargins(x0)
chisq.test(x0)
論理的には,900世帯は,ドラマ1も2も見た世帯,1か2の一方のみ見た世帯,いずれも見なかった世帯の4通りに分類される。ドラマ1を見た/見ていない,ドラマ2を見た/見ていないの2行×2列の分割表で表現される筈である。これが対応のある場合の比率の差を考える出発点である。
しかし,視聴率調査では,そこまで詳しい情報は一般には公開されていないので,我々にはこの分割表は作る事が出来ない。
そこで以下では,3つの対照的な分割表xa, xb, xcについて分析して比較しよう。参考までにそのままカイ二乗検定を行った結果(2行2列なのでデフォルトでイェーツの連続性修正付き)も添えているが,これは「ドラマ1の視聴とドラマ2の視聴は全く関連が無い」と云うゼロ仮説の検定であり,母比率に差があると言えるかどうかの検定とは全く別物である事に注意して欲しい。
3つの分割表は全て周辺度数は(当然)同一であるが,分割表の中身は大きく異なる。
n <- 900
p1 <- .160; p2 <- .130
n1 <- n*p1; n2 <- n*p2
# ドラマ2を見た人は全てドラマ1も見たと云う極端なケースa
xa <- matrix(c((a11 <- min(n1, n2)), n2-a11, n1-a11, n-(n1+n2-a11)), ncol=2)
addmargins(xa)
chisq.test(xa)
# ほぼ完全独立の極端なケースb
xb <- matrix(c((b11 <- 19), n2-b11, n1-b11, n-(n1+n2-b11)), ncol=2)
addmargins(xb)
chisq.test(xb)
# 完全分離の極端なケースc
xc <- matrix(c((c11 <- 0), n2-c11, n1-c11, n-(n1+n2-c11)), ncol=2)
addmargins(xc)
chisq.test(xc)
p1 <- .160; p2 <- .130
n1 <- n*p1; n2 <- n*p2
# ドラマ2を見た人は全てドラマ1も見たと云う極端なケースa
xa <- matrix(c((a11 <- min(n1, n2)), n2-a11, n1-a11, n-(n1+n2-a11)), ncol=2)
addmargins(xa)
chisq.test(xa)
# ほぼ完全独立の極端なケースb
xb <- matrix(c((b11 <- 19), n2-b11, n1-b11, n-(n1+n2-b11)), ncol=2)
addmargins(xb)
chisq.test(xb)
# 完全分離の極端なケースc
xc <- matrix(c((c11 <- 0), n2-c11, n1-c11, n-(n1+n2-c11)), ncol=2)
addmargins(xc)
chisq.test(xc)


対応のある2群の母比率の検定では,「ドラマ1もドラマ2も見た」人達,「両方とも見なかった」人達は考慮に入れない。この人達は母比率に差をもたらす事が定義上無いからである。注目されるのは,「ドラマ1は見たがドラマ2は見なかった」人達(1行2列)と「ドラマ1は見なかったがドラマ2は見た」人達(2行1列)だけである。例えば分割表xaでは1行2列は27人,2行1列は0人,合計で27人であるが,「この人達は本来,いずれのセルに入るかは五分五分であり,この標本ではたまたま1行2列に27人が入った」と云う確率が小さいか,そうでないかを検定する。分割表xbでは125人と98人で合計223人,分割表xcでは144人と117人で合計261人が対象である。
標準正規分布を用いた検定
ドラマ1の視聴世帯数をn1,ドラマ2の視聴世帯数をn2,両方のドラマを見た世帯数をa11(またはb11, c11)とすると,ドラマ1だけを見た世帯数(1行2列)はn1-a11(またはn1-b11, n1-c11),ドラマ2だけを見た世帯数(2行1列)はn2-a11(またはn2-b11, n2-c11)であり,いずれか一方だけを見た世帯の総数はn1+n2-2*a11(またはn1+n2-2*b11, n1+n2-2*c11)となる。標準正規分布による検定では,1行2列(または2行1列でも良い)に入る人数は本来はn1+n2-2*a11の半分であるが(=期待値),それが偶然にn1-a11になったと云う確率が小さいか否かを考える。この人数の標準誤差はsqrt((n1+n2-2*a11)*.5*(1-.5))となる事が分かっているので(2項分布の平均と分散),確率的に変動する「1行2列の人数」を標準化すると((n2-n11)-.5*(n1+n2-2*n11))/sqrt((n1+n2-2*n11)*.5*.5)となる。これが標準正規分布に従う事を利用して検定を行う。
以下に3つの場合全てについてこの標準正規分布検定を示した。後でマクネマー検定との関係を示す為に,標準正規変量を二乗した値(自由度1のカイ二乗変量になる)も示してある。
# 標準正規変量によるz検定.標準誤差sqrt(n*p*(1-p))は二項分布の成功回数のもの
za <- ((n2-a11)-.5*(n1+n2-2*a11))/sqrt((n1+n2-2*a11)*.5*.5); za
2*(1-pnorm(abs(za), 0, 1)) # 標準正規分布の両側有意確率
za^2 # 標準正規変量の二乗=自由度1のカイ二乗変量
zb <- ((n2-b11)-.5*(n1+n2-2*b11))/sqrt((n1+n2-2*b11)*.5*.5); zb
2*(1-pnorm(abs(zb), 0, 1)) # 標準正規分布の両側有意確率
zb^2 # 標準正規変量の二乗=自由度1のカイ二乗変量
zc <- ((n2-c11)-.5*(n1+n2-2*c11))/sqrt((n1+n2-2*c11)*.5*.5); zc
2*(1-pnorm(abs(zc), 0, 1)) # 標準正規分布の両側有意確率
zc^2 # 標準正規変量の二乗=自由度1のカイ二乗変量
2*(1-pnorm(abs(za), 0, 1)) # 標準正規分布の両側有意確率
za^2 # 標準正規変量の二乗=自由度1のカイ二乗変量
zb <- ((n2-b11)-.5*(n1+n2-2*b11))/sqrt((n1+n2-2*b11)*.5*.5); zb
2*(1-pnorm(abs(zb), 0, 1)) # 標準正規分布の両側有意確率
zb^2 # 標準正規変量の二乗=自由度1のカイ二乗変量
zc <- ((n2-c11)-.5*(n1+n2-2*c11))/sqrt((n1+n2-2*c11)*.5*.5); zc
2*(1-pnorm(abs(zc), 0, 1)) # 標準正規分布の両側有意確率
zc^2 # 標準正規変量の二乗=自由度1のカイ二乗変量

本来半々の筈が27対0になる事はおよそ偶然とは考えられないが,偶然に125対98(約1.28倍)や144対117(約1.23倍)になる事は20回に1回よりは多く起こり得るのでそれ程おかしくはないと云う結果になっている。
マクネマー検定(McNemar test)
こうした検定を行う場合,よく紹介されているのはマクネマー検定と云う方法である。Rにも mcnemar( )関数が用意されているが,2行2列の分割表の独立性の検定のイェーツの連続性修正と同様,デフォルトでは連続性修正を行う。以下ではa,b,cのそれぞれについて連続性の修正を行わない場合と行う場合の両方の結果を示す。
# マクネマー検定
mcnemar.test(xa, correct=F)
mcnemar.test(xa)
mcnemar.test(xb, correct=F)
mcnemar.test(xb)
mcnemar.test(xc, correct=F)
mcnemar.test(xc)
mcnemar.test(xa, correct=F)
mcnemar.test(xa)
mcnemar.test(xb, correct=F)
mcnemar.test(xb)
mcnemar.test(xc, correct=F)
mcnemar.test(xc)


これも自動的に検定を行ってくれるのでとても便利であるが,カイ二乗検定である事以外はここからはよく分からない。
ただ,先の標準正規分布による検定のp値及びカイ二乗値(標準正規変量の二乗)と(修正なしの)マクネマー検定の結果を見比べると,3つとも一致している事が確認出来る。マクネマー検定の方は連続性の修正を行う事は出来るが,基本的には同じ様な事をしているのだと理解する事が出来る(検定結果については最後に纏める)。
2項検定(Binomial test)
以上二つの考え方の基本になっているのは,いずれか一方だけを見た世帯の総数n1+n2-2*a11(またはn1+n2-2*b11, n1+n2-2*c11)は成功確率.5の2項分布に従って1行2列のセルもしくは2行1列のセルに割り当てられると云う考えであり,実際の結果が偶然の範囲内だと言えるかどうかを調べるのが検定である。であれば,最初から素直に2項検定を行うのが分かり易い。Rには2項検定を簡単に実行する binom.test( )関数がある。
# 2項検定
binom.test(n1-a11, n1+n2-2*a11, p=.5)
binom.test(n1-b11, n1+n2-2*b11, p=.5)
binom.test(n1-c11, n1+n2-2*c11, p=.5)
binom.test(n1-a11, n1+n2-2*a11, p=.5)
binom.test(n1-b11, n1+n2-2*b11, p=.5)
binom.test(n1-c11, n1+n2-2*c11, p=.5)


number of trials が問題の2つのセルの度数合計,number of successes が1行2列の実際の度数,そこに当てはまる確率が.5である。 p-value がその2項検定の結果の有意確率である。やはりxaでは高度に有意,xb,xcでは5%で有意にならない。
最後のxcの場合を用いて,この2項検定をもう少し丁寧に確認してみよう。
# 2項検定の内容の確認
pbinom(143, size=261, prob=.5, lower.tail=F) # 144以上に大きくなる確率
pbinom(261-144, size=261, prob=.5) # 117以下に小さくなる確率
pbinom(261-144, size=261, prob=.5)*2 # 両側確率
pbinom(143, size=261, prob=.5, lower.tail=F) # 144以上に大きくなる確率
pbinom(261-144, size=261, prob=.5) # 117以下に小さくなる確率
pbinom(261-144, size=261, prob=.5)*2 # 両側確率

多い方のセルの度数以上になるか,もしくは少ない方のセルの度数以下になる確率の合計が両側有意確率であり,これを pbinom( )関数で求めると,上の binom.test( )の結果に一致している。全部自動で実行してくれる関数はとても便利であるが,少なくとも最初は,それが何をやっているのかをこの様に確認しながら理解していく様にしよう。
最後に,以上の数種類の検定結果を簡単に纏めて比較しておく。
| 各種検定での有意確率・一覧 | |||
| 検定方法 | 分割表(xa) | 分割表(xb) | 分割表(xc) |
| 標準正規検定 | 2.034555e-07 | .07059814 | .09467072 |
| マクネマー検定(修正なし) | 2.035e-07 | .0706 | .09467 |
| マクネマー検定(修正あり) | 5.624e-07 | .08167 | .1075 |
| 2項検定 | 1.49e-08 | .08144 | .1074 |
連続性修正を行ったマクネマー検定は2項検定の結果にかなり近い。Rでは連続性修正を行うのがデフォルトでもあり,簡単に「対応のある2群の母比率の差の検定」を行う為に適してはいるが,2項検定も同じくらい簡単に実行出来るので,敢えてマクネマー検定を行う意味があるかどうかは不明である。
Copyright (C) 2016-2017 SUGINO Isamu All Rights Reserved. design by tempnate

