杉野 勇 (SUGINO Isamu) お茶の水女子大学・人間発達科学専攻・応用社会学コース担当
『入門・社会統計学』サポートウェブ |
|
第13章 階層構造のあるデータの分析
統計分析は，それぞれのデータが，相互に関連せず，独立にランダムサンプリングされている事を前提にしている事が多い。しかし実際には，空間的纏まりや時間的関連を持ったデータが相互に相関している事がある。それらがあたかも相互に相関していないかの様に分析する事は誤った結果に導く可能性もある。ここでは，空間的纏まりをもったデータに対するマルチレヴェル分析，時間的な系列をなすデータに対するイヴェント・ヒストリー分析の考え方のごく初歩を解説する。1-1 級内相関係数(ICC)
固定効果(fixed effect)と変量効果(random effect)とは
テクスト本文ではマルチレヴェル分析について詳しく説明する紙幅が無かったので，ここで少し補う事にする。まずは方程式の観点から説明する。以下に，通常の回帰分析との違いを段階的に示した。
通常の最も単純な回帰分析では，対象者が幾つかのグループに分属している（ネストしている）場合でも，切片と回帰係数は全員に共通だと仮定する。これが下の「通常の回帰分析」である。切片（定数項）と傾き（回帰係数）は，個人iによっても集団jによっても変化しない定数である。
これに，集団による違いを少し考慮してみる。切片だけは集団によって異なるとしよう。最も簡単なのは，集団jの違いを示すダミー変数を追加投入し，そのダミー変数の係数を集団固有の切片の効果とするモデルである。分析を行えば各集団の効果はそれぞれ具体的な定数値として計算される。これを固定効果と呼ぶ。
但しこの方法では，集団の数が多くなると，推定すべき定数（固定効果）の数も多くなる。「どの集団ではどの程度の効果があるのか」を具体的に知りたいならこうすべきだが，「集団によってどれくらい異なるのか」だけが分かれば良い場合は，それぞれの集団ごとに具体的な効果の値を計算しなくても良い。集団による切片の違いのバラつき具合（分散）だけが分かれば良い。この時，定数項γに，集団による誤差項uを加えて，この誤差分散を推定するだけで済ませれば，集団の数が増えても推定すべきものは増えずに都合が良い。この誤差項uを変量効果（ランダム効果）と言う。
同じ事は，傾き（回帰係数）についても言える。集団ごとに異なる定数の回帰係数βを求めるのではなく，基準となる回帰係数の値γから集団によってどれくらいの変動があるのかを誤差項uの分散によって検討するのである。
切片（定数項）だけに（集団による）ランダム効果を設定するモデルを「ランダム切片モデル」，傾き（回帰係数）だけにランダム効果を設定するモデルを「ランダム傾きモデル」（或はランダム係数モデル），両方にランダム効果を設定するモデルを「ランダム切片・ランダム傾きモデル」と呼んだりする。
ランダム切片モデルのグラフ解説
方程式の次は，グラフで理解しよう。仮に大きさ300人のサンプルが，30のグループ（それぞれ10人が所属）のネスト構造を持っているとする（架空のシミュレイションデータ）。階層性を無視して，全300人で単純に散布図を描いて回帰直線を引いたのが次の図である。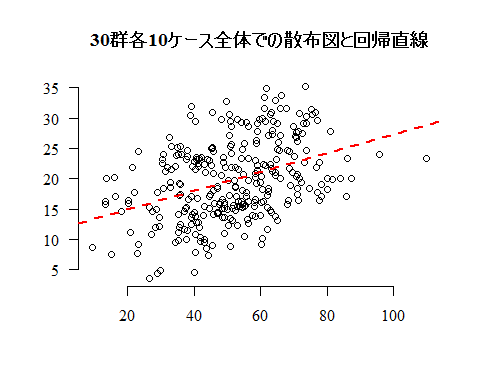
このデータは実際には群によって切片に差がある母集団から発生させている（傾きは群で共通）。群ごとに回帰直線を描き分けたのが次の図である。比較の為に上の回帰直線も描いている。また傾きは本来は各群で共通(.20)であるが，標本データには誤差がある為，標本回帰係数（直線の傾き）は群によって多少ばらついている。
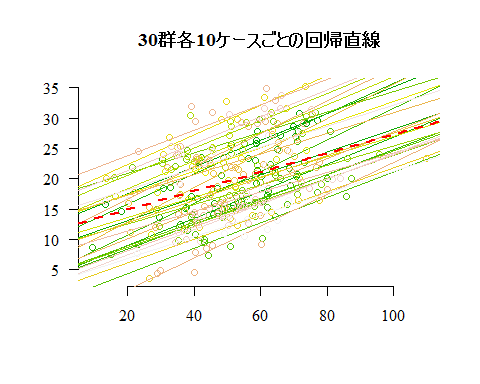
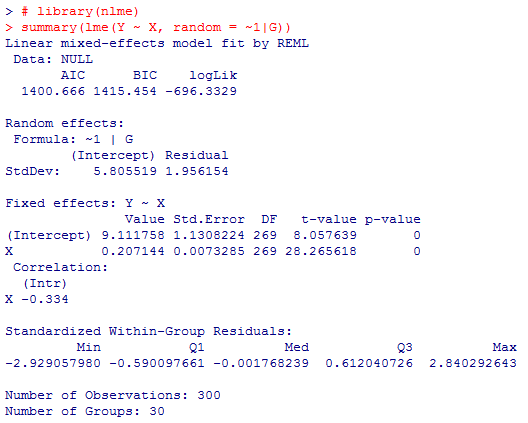
単純に回帰分析を行う為には，lm( )関数を用いれば良い。マルチレヴェル分析を行うには，nlmeパッケイジのlme( )関数を使う。上のシミュレイションデータを，lm( )とlme( )で分析した結果が下記であり，傾きを表すXの係数が，階層性を無視したlm( )では.155，lme( )のランダム切片モデルでは.207となっている（後者の方が本来の.20に近いが，偶然誤差にも依存するので，必ずそうなる保証がある訳では無い）。もう一点大きく違うのは標準誤差の値であり，階層性を無視したlm( )では標準誤差が大きく，その結果t値が相対的に小さくなり，有意確率も相対的には大きくなる。標準誤差が大きいと云う事は，回帰係数の信頼区間を求めた場合も，区間がかなり広くなると云う事を意味する。このlm( )の結果からは95%信頼区間は.113〜.197となるが，lme( )の結果からは.193〜.222である。係数の点推定値や有意確率だけを見ていると気付きにくいが，推定の精度がかなり異なる。
尚，Rでマルチレヴェル分析を行う有名な関数には他に，lme4パッケイジのlmer( )関数もある。コマンドの書き方や出力の仕方に多少の違いはあるが，分析結果はlme( )と一致している。
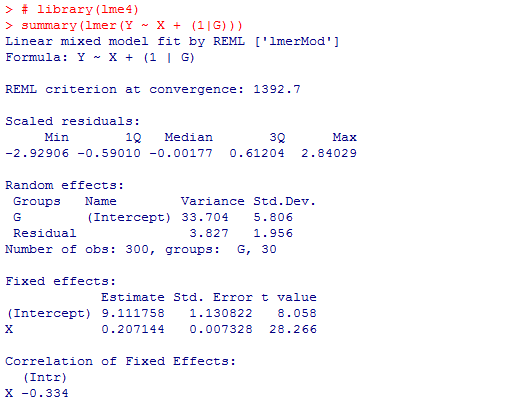
以上がテクストに収められなかった説明の補遺であり，次からテクスト本文の内容に戻る。
級内相関係数(ICC; Intra-class Correlation Coefficient)
マルチレヴェル分析をすべきか否かの判断は，しばしば級内相関係数(ICC，グループの内部でどの程度相関関係が存在してしまっているか)を見て行う。級内相関係数は，ピアソンの積率相関係数の様なものとイメージするよりも，分散分析における級内分散と級間分散，或は一般線型モデルにおける分散説明率の様なものと考えると分かる。級内分散と級間分散の和に対して，級内分散がどの程度の割合になるかを示している。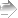
清水裕士 2014「マルチレベルモデル講習会 理論編」(2016年11月19日閲覧)
data01$male <- c(1, 0)[data01$sex] # 男性ダミーの作成
data01$site <- factor(floor(data01$id/100)) # 地点変数の作成
# 初歩的な線型モデルで切片だけのモデル
lm00 <- lm(fincome ~ 1, data=data01); summary(lm00)
mean(data01$fincome, na.rm=T) # 単なる平均値の計算
# 地点変数site（要因型）を「固定効果」として独立変数に投入した線型モデル
lm00b <- lm(fincome ~ site, data=data01); summary(lm00b)
（以下の出力の一行目は male <- ではなく data01$male <- の間違いであるが，結果に違いは無いので其の儘にしてある。）data01$site <- factor(floor(data01$id/100)) # 地点変数の作成
# 初歩的な線型モデルで切片だけのモデル
lm00 <- lm(fincome ~ 1, data=data01); summary(lm00)
mean(data01$fincome, na.rm=T) # 単なる平均値の計算
# 地点変数site（要因型）を「固定効果」として独立変数に投入した線型モデル
lm00b <- lm(fincome ~ site, data=data01); summary(lm00b)
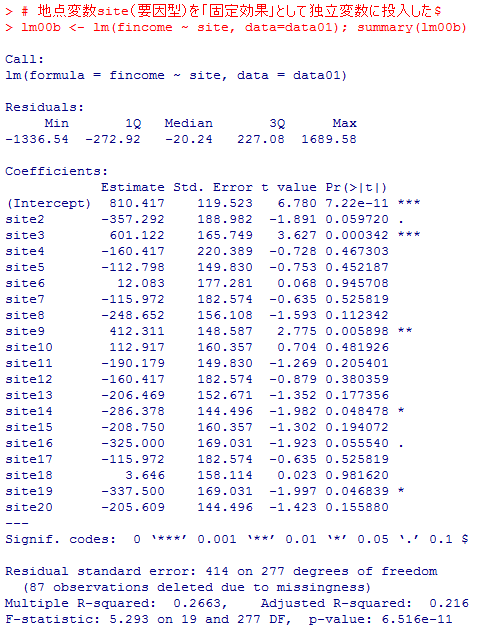
自由度調整済み分散説明率が.216もある。地点変数がかなり世帯年収に対して説明力を持っている事が伺われる
地点変数を，nlmeパッケイジのlme( )関数を用いて，変量効果として投入してみよう。地点それぞれの具体的な効果は推定せずに，地点間でのバラつき（級間変動）だけを分析するのである。
library(nlme)
lme00 <- lme(fincome ~ 1, random = ~1|site, data=data01, na.action="na.omit")
summary(lme00)
VarCorr(lme00) # 級間分散と級内分散
var1 <- as.numeric(VarCorr(lme00)); var1[1]/sum(var1[1:2]) # ICCの計算
lme00 <- lme(fincome ~ 1, random = ~1|site, data=data01, na.action="na.omit")
summary(lme00)
VarCorr(lme00) # 級間分散と級内分散
var1 <- as.numeric(VarCorr(lme00)); var1[1]/sum(var1[1:2]) # ICCの計算
着目するのは Random effects（変量効果）のStdDev（標準偏差）の欄であり，(Intercept)が級間，Residualが級内を示す。ここから級内相関係数ICCを手計算する事も出来るが，上記の様にスクリプトを書いておけば自動で計算してくれる。ここでは21.9%となり，通常10%を超えるならマルチレヴェル分析を検討した方が良いとの基準を超えている。よって以下でもマルチレヴェルモデルにて世帯年収の分析を行う。
ICCの計算方法
lme( )関数の場合を例にとると，計算方法（推定方法）として「最尤法(Maximum Liklihood)」(method="ML")と「制限付き最尤法(REstricted Maximum Liklihood)」(method="REML")があり，計算結果は微妙に異なる。デフォルトはREMLである。lmer( )関数ではREML=TRUE|FALSEのオプションで切り替えられる。MLで解くかREMLで解くかによって結果は若干変わる。また，lme(, method="ML")とlmer(, REML=FALSE)では極めて僅かに計算結果が異なる場合も見られた。またICCを計算したりICCの信頼区間を求めるパッケイジICCがあり，その中の関数 ICCest( ) によってもICCを求める事が出来るが，バランスデータ（各群のケース数が等しい）かそうでないかによって，lme( )とも多少計算結果が異なったりする。
# バランスデータの場合のICC計算例
VarCorr(lme01 <- lme(Y ~ 1, random = ~1|G))
ICC1 <- as.numeric(VarCorr(lme01))
ICC1[1]/sum(ICC1[1:2]) # lme( , method="REML")
ICCest(x=factor(G), y=Y) # library(ICC)
# アンバランスデータの場合のICC計算例
VarCorr(lme02 <- lme(fincome ~ 1, random = ~1|site, data=data01, na.action="na.omit"))
ICC2 <- as.numeric(VarCorr(lme02))
ICC2[1]/sum(ICC2[1:2]) # lme( , method="REML")
ICCest(x=factor(site), y=fincome, data=data01) # library(ICC)
VarCorr(lme01 <- lme(Y ~ 1, random = ~1|G))
ICC1 <- as.numeric(VarCorr(lme01))
ICC1[1]/sum(ICC1[1:2]) # lme( , method="REML")
ICCest(x=factor(G), y=Y) # library(ICC)
# アンバランスデータの場合のICC計算例
VarCorr(lme02 <- lme(fincome ~ 1, random = ~1|site, data=data01, na.action="na.omit"))
ICC2 <- as.numeric(VarCorr(lme02))
ICC2[1]/sum(ICC2[1:2]) # lme( , method="REML")
ICCest(x=factor(site), y=fincome, data=data01) # library(ICC)
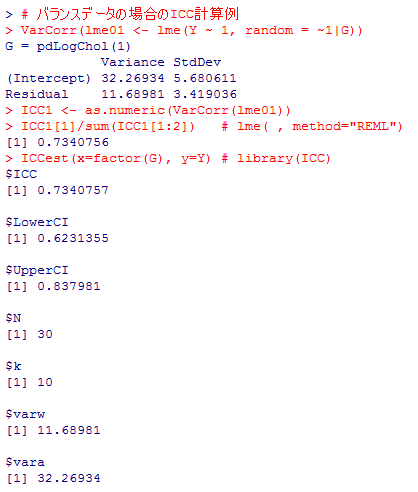
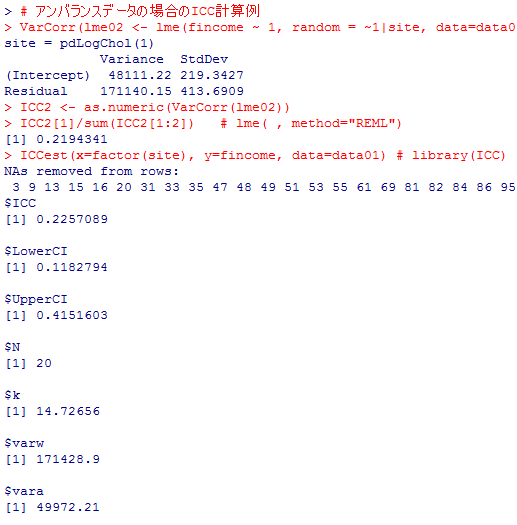
上の例を見る限りでは，実質的な判断を分ける程の大きな違いではないので，用いた計算法や関数などを明記しておけばそれ程気にする必要は無いだろう。
1-2 マルチレヴェルモデル(multilevel model)
まずは比較の為に，通常の重回帰分析の結果を確認しておく。
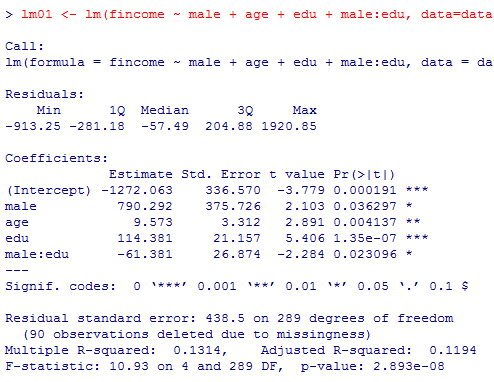
男性の場合は，世帯年収 = -1272 + 790.292 + 9.6*age + (114.381-61.381)*edu =-482 + 9.6*age + 53*edu
女性の場合は，世帯年収 = -1272 + 9.6*age + 114.381*edu
男性と女性で切片と，教育年数の効果が異なる。女性は，男性に比べて教育の効果が2倍以上大きい。具体的なケースで世帯年収の予測値を求めてみよう。
次に，地点変数を変量効果（ランダム効果）として投入したマルチレヴェルモデルを分析する。
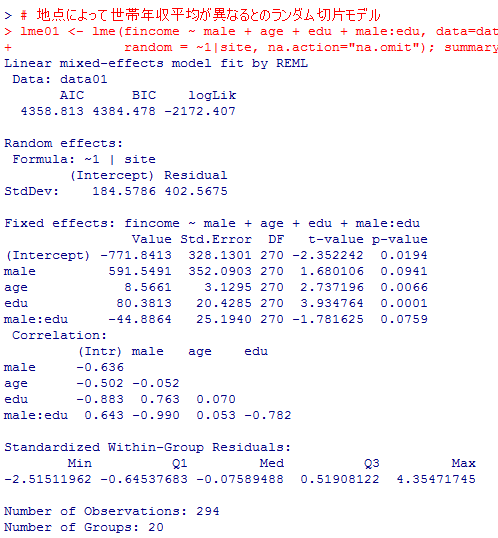
どのパラメタ推定値も上のlm01よりも小さくなり，男性ダミー，男性ダミーと教育年数の交互作用は5%水準で有意ではなくなった。つまり，男女関係なく世帯年収は年齢と教育年数で予測されると云う結果になった。級内相関係数は.174となる。
改めて有意になった変数だけで分析してみよう。
独立変数を二つ除外したが，マクファデンの疑似決定係数はそれほど低下していない。
ランダム係数モデル，ランダム切片・ランダム係数モデルは余り良い結果が得られなかったのでスクリプトだけ紹介しておく。
RとStanでマルチレヴェル回帰分析を行った例を，このサポートウェブの〔付録〕3-3で紹介しています。
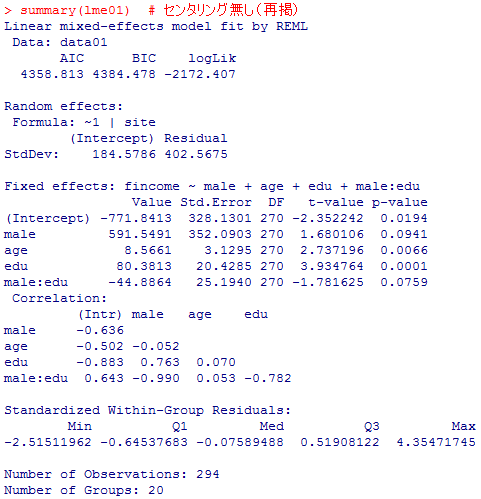
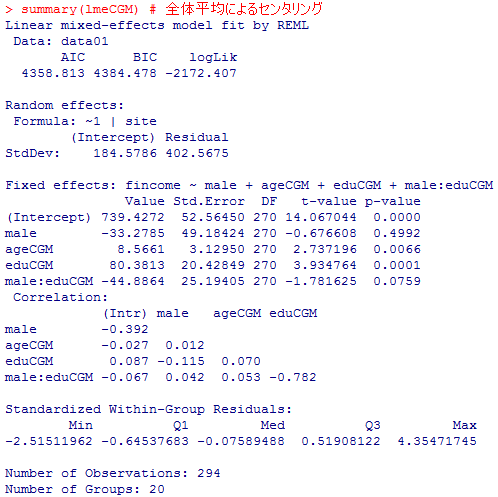
センタリング無しの結果と，全体平均でセンタリングした結果はよく似ている。また，3つとも男性ダミー，男性ダミーと教育年数の交互作用が5%で有意にならない点も共通している。おおまかには似た様な分析結果であるが，有意になった説明変数のパラメタ推定値を見ると，全体平均センタリングの場合の教育年数の効果に比べて，地点平均センタリングの場合の教育年数の効果はやや小さい値となっている。
# マルチレヴェルではない通常の重回帰分析
lm01 <- lm(fincome ~ male + age + edu + male:edu, data=data01); summary(lm01)
lm01 <- lm(fincome ~ male + age + edu + male:edu, data=data01); summary(lm01)
男性の場合は，世帯年収 = -1272 + 790.292 + 9.6*age + (114.381-61.381)*edu =-482 + 9.6*age + 53*edu
女性の場合は，世帯年収 = -1272 + 9.6*age + 114.381*edu
男性と女性で切片と，教育年数の効果が異なる。女性は，男性に比べて教育の効果が2倍以上大きい。具体的なケースで世帯年収の予測値を求めてみよう。
次に，地点変数を変量効果（ランダム効果）として投入したマルチレヴェルモデルを分析する。
# 地点によって世帯年収平均が異なるとのランダム切片モデル
lme01 <- lme(fincome ~ male + age + edu + male:edu, data=data01,
random = ~1|site, na.action="na.omit"); summary(lme01)
lme01 <- lme(fincome ~ male + age + edu + male:edu, data=data01,
random = ~1|site, na.action="na.omit"); summary(lme01)
どのパラメタ推定値も上のlm01よりも小さくなり，男性ダミー，男性ダミーと教育年数の交互作用は5%水準で有意ではなくなった。つまり，男女関係なく世帯年収は年齢と教育年数で予測されると云う結果になった。級内相関係数は.174となる。
改めて有意になった変数だけで分析してみよう。
# 年齢と教育年数（固定効果）と地点（変量効果）だけで世帯年収を説明する
lme02 <- lme(fincome ~ age + edu , data=data01,
random = ~1|site, na.action="na.omit"); summary(lme02)
VarCorr(lme02) # 級間分散と級内分散
var1 <- as.numeric(VarCorr(lme02)); var1[1]/sum(var1[1:2]) # ICCの計算
# 疑似決定係数の比較
# glm( )関数による一般化線型モデル（恒等リンク関数・正規分布）
null <- glm(fincome ~ 1, data=data01, family = gaussian(link = "identity"))
L0 <- logLik(null); Ll <- logLik(lme01); Ls <- logLik(lme02)
1-Ll[1]/L0[1] # lme01のMcFadden
1-Ls[1]/L0[1] # lme02のMcFadden
lme02 <- lme(fincome ~ age + edu , data=data01,
random = ~1|site, na.action="na.omit"); summary(lme02)
VarCorr(lme02) # 級間分散と級内分散
var1 <- as.numeric(VarCorr(lme02)); var1[1]/sum(var1[1:2]) # ICCの計算
# 疑似決定係数の比較
# glm( )関数による一般化線型モデル（恒等リンク関数・正規分布）
null <- glm(fincome ~ 1, data=data01, family = gaussian(link = "identity"))
L0 <- logLik(null); Ll <- logLik(lme01); Ls <- logLik(lme02)
1-Ll[1]/L0[1] # lme01のMcFadden
1-Ls[1]/L0[1] # lme02のMcFadden
独立変数を二つ除外したが，マクファデンの疑似決定係数はそれほど低下していない。
ランダム係数モデル，ランダム切片・ランダム係数モデルは余り良い結果が得られなかったのでスクリプトだけ紹介しておく。
summary(lme(fincome ~ male + age + edu + male:edu, random = ~ 0+ edu|site,
data=data01, na.action="na.omit")) # ランダム係数モデル
summary(lme(fincome ~ male + age + edu + male:edu, random = ~ edu|site,
data=data01, na.action="na.omit")) # ランダム切片・ランダム係数モデル
data=data01, na.action="na.omit")) # ランダム係数モデル
summary(lme(fincome ~ male + age + edu + male:edu, random = ~ edu|site,
data=data01, na.action="na.omit")) # ランダム切片・ランダム係数モデル
RとStanでマルチレヴェル回帰分析を行った例を，このサポートウェブの〔付録〕3-3で紹介しています。
センタリング(centering)
本文では，本来は重要な「センタリング」については言葉で紹介しているだけなので，ここで分析例を一つ紹介して補っておく。
# 先のlme01の分析例でそれぞれを求めるスクリプト例
data01$ageCGM <- data01$age - mean(data01$age, na.rm=T) # 年齢のCGM
data01$eduCGM <- data01$edu - mean(data01$edu, na.rm=T) # 教育年数のCGM
ageM <- tapply(data01$age, data01$site, mean, na.rm=T) # 集団（地点site）ごとの平均年齢ヴェクトル
data01$ageCWC <- data01$age - ageM[data01$site] # 年齢のCWC
eduM <- tapply(data01$edu, data01$site, mean, na.rm=T) # 集団ごとの平均教育年数ヴェクトル
data01$eduCWC <- data01$edu - eduM[data01$site] # 教育年数のCWC
lmeCGM <- lme(fincome ~ male + ageCGM + eduGM + male:eduCGM, data=data01,
random = ~1|site, na.action="na.omit") # CWCを用いたマルチレヴェル
lmeCWC <- lme(fincome ~ male + ageCWC + eduCWC + male:eduCWC, data=data01,
random = ~1|site, na.action="na.omit") # CWCを用いたマルチレヴェル
summary(lme01) # センタリング無し（再掲）
summary(lmeCGM) # 全体平均によるセンタリング
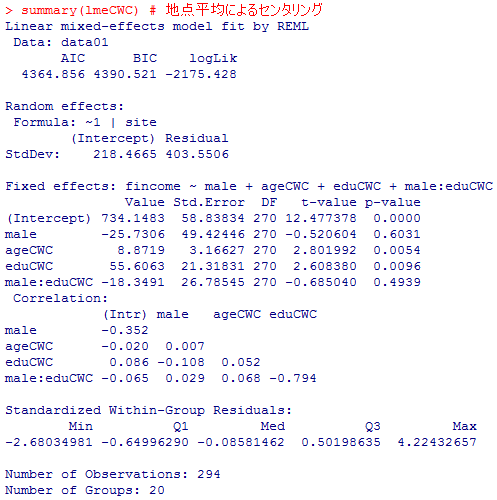
summary(lmeCWC) # 地点平均によるセンタリング
data01$ageCGM <- data01$age - mean(data01$age, na.rm=T) # 年齢のCGM
data01$eduCGM <- data01$edu - mean(data01$edu, na.rm=T) # 教育年数のCGM
ageM <- tapply(data01$age, data01$site, mean, na.rm=T) # 集団（地点site）ごとの平均年齢ヴェクトル
data01$ageCWC <- data01$age - ageM[data01$site] # 年齢のCWC
eduM <- tapply(data01$edu, data01$site, mean, na.rm=T) # 集団ごとの平均教育年数ヴェクトル
data01$eduCWC <- data01$edu - eduM[data01$site] # 教育年数のCWC
lmeCGM <- lme(fincome ~ male + ageCGM + eduGM + male:eduCGM, data=data01,
random = ~1|site, na.action="na.omit") # CWCを用いたマルチレヴェル
lmeCWC <- lme(fincome ~ male + ageCWC + eduCWC + male:eduCWC, data=data01,
random = ~1|site, na.action="na.omit") # CWCを用いたマルチレヴェル
summary(lme01) # センタリング無し（再掲）
summary(lmeCGM) # 全体平均によるセンタリング
summary(lmeCWC) # 地点平均によるセンタリング
センタリング無しの結果と，全体平均でセンタリングした結果はよく似ている。また，3つとも男性ダミー，男性ダミーと教育年数の交互作用が5%で有意にならない点も共通している。おおまかには似た様な分析結果であるが，有意になった説明変数のパラメタ推定値を見ると，全体平均センタリングの場合の教育年数の効果に比べて，地点平均センタリングの場合の教育年数の効果はやや小さい値となっている。
2-1 パーソンピリオドデータ(Person-Period data)
まずは例示用に作成した模擬データ(person level data)の作成スクリプトを示そう。意味が分からなくても問題はない。乱数成分があるので，実行するたびに結果は変わる。
次は，この通常のパーソンレヴェルデータを，パーソン・ピリオドデータに変換する方法を紹介する。
まずは，上で生成したパーソンレヴェルデータを，ワイド型データに変換する。
やや難易度が高いが，それぞれ何をしているか分かる様になれば，自分で応用して使用する事が出来る様になるだろう（或はもっと簡単な方法が何処かにあるかも知れないので，Rについては常によく情報を収集しているととても楽が出来る様になる）。
さて，次にこのwide型データをlong型データ，つまりperson-period dataに変換する。不要になるincome05をdropしておく。
なお，必要があるかどうかわからないが，reshape( )関数は，ワイド型からロング型への変換も可能である。v.names=で時間依存変数を指定すると，それ以外の変数は時間不変変数だとみなされる。不要な変数は後から列削除するとよい。
n <- 10; t <- 5
pid <- 1:n
age01 <- sample(25:59, size=n, replace=TRUE)
edu <- sample(c(9, 12, 14, 16, 18), size=n, replace=TRUE, prob=c(.05, .4, .1, .35, .1))
income <- matrix(numeric(n*t), ncol=t, nrow=n)
income[,1] <- edu * 20 + rbinom(n, size=10, prob=.4)*80 # incomeはeduだけに依存
for (i in 2:t) {
income[, i] <- income[, i-1] + (rbinom(n, size=40, prob=.5)-20)*10
}
# event経験時点を，年齢，教育，収入に関連させて定義
logit0 <- t*(.08*(age01-mean(age01))/sd(age01) + .16*(edu-mean(edu))/sd(edu) + .18*(income[,1]-mean(income[,3]))/sd(income[,3]))
logit0 <- ceiling(logit0 + abs(min(logit0))+1.1)
t_event <- c(1:5)[logit0]
data_person <- data.frame(cbind(pid, age01, edu, income, t_event))
colnames(data_person)[4:(3+t)] <- sprintf("income%02d", c(1:t))
data_person # ダミーデータの出来上がり
pid <- 1:n
age01 <- sample(25:59, size=n, replace=TRUE)
edu <- sample(c(9, 12, 14, 16, 18), size=n, replace=TRUE, prob=c(.05, .4, .1, .35, .1))
income <- matrix(numeric(n*t), ncol=t, nrow=n)
income[,1] <- edu * 20 + rbinom(n, size=10, prob=.4)*80 # incomeはeduだけに依存
for (i in 2:t) {
income[, i] <- income[, i-1] + (rbinom(n, size=40, prob=.5)-20)*10
}
# event経験時点を，年齢，教育，収入に関連させて定義
logit0 <- t*(.08*(age01-mean(age01))/sd(age01) + .16*(edu-mean(edu))/sd(edu) + .18*(income[,1]-mean(income[,3]))/sd(income[,3]))
logit0 <- ceiling(logit0 + abs(min(logit0))+1.1)
t_event <- c(1:5)[logit0]
data_person <- data.frame(cbind(pid, age01, edu, income, t_event))
colnames(data_person)[4:(3+t)] <- sprintf("income%02d", c(1:t))
data_person # ダミーデータの出来上がり
次は，この通常のパーソンレヴェルデータを，パーソン・ピリオドデータに変換する方法を紹介する。
まずは，上で生成したパーソンレヴェルデータを，ワイド型データに変換する。
## person-level dataからwideへ
age <- matrix(numeric(n*t), ncol=t, nrow=n) # 時間依存の年齢変数の空箱
age[,1] <- age01 # 最初の時点の年齢
for (j in 2:t) {
age[,j] <- age[,j-1] + 1
} # 作成した結果を見たければ，コンソール画面で age とする。
event <- matrix(rep(NA, n*t), ncol=t, nrow=n) # event生起変数の空箱
for (i in 1:n) {
if (!is.na(t_event[i])) event[i, 1:min(t, t_event[i]-1)] <- 0; event[i, t_event[i]] <- 1
if (is.na(t_event[i])) event[i, 1:t] <- 0
} # 作成した結果を見たければ，コンソール画面で event とする。
data_wide <- data.frame(cbind(data_person[,c(1, 3:(3+t))], age, event))
colnames(data_wide)[(2+t+1):(2+t+t)] <- sprintf("age%02d", c(1:t))
colnames(data_wide)[(2+2*t+1):(2+2*t+t)] <- sprintf("event%02d", c(1:t))
data_wide # wide型データの確認
age <- matrix(numeric(n*t), ncol=t, nrow=n) # 時間依存の年齢変数の空箱
age[,1] <- age01 # 最初の時点の年齢
for (j in 2:t) {
age[,j] <- age[,j-1] + 1
} # 作成した結果を見たければ，コンソール画面で age とする。
event <- matrix(rep(NA, n*t), ncol=t, nrow=n) # event生起変数の空箱
for (i in 1:n) {
if (!is.na(t_event[i])) event[i, 1:min(t, t_event[i]-1)] <- 0; event[i, t_event[i]] <- 1
if (is.na(t_event[i])) event[i, 1:t] <- 0
} # 作成した結果を見たければ，コンソール画面で event とする。
data_wide <- data.frame(cbind(data_person[,c(1, 3:(3+t))], age, event))
colnames(data_wide)[(2+t+1):(2+t+t)] <- sprintf("age%02d", c(1:t))
colnames(data_wide)[(2+2*t+1):(2+2*t+t)] <- sprintf("event%02d", c(1:t))
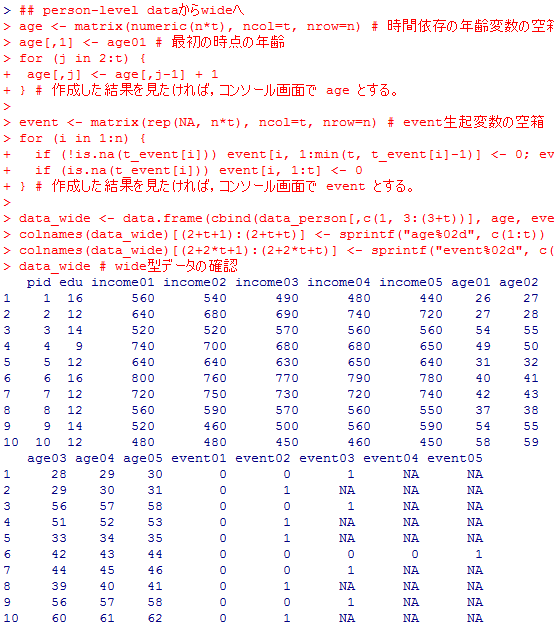
data_wide # wide型データの確認
やや難易度が高いが，それぞれ何をしているか分かる様になれば，自分で応用して使用する事が出来る様になるだろう（或はもっと簡単な方法が何処かにあるかも知れないので，Rについては常によく情報を収集しているととても楽が出来る様になる）。
さて，次にこのwide型データをlong型データ，つまりperson-period dataに変換する。不要になるincome05をdropしておく。
## reshape( )関数を使用して，wideからlongへの変換
data_wide$income00 <- NA # 観察期間前のラグ変数の準備
data_long <- reshape(data_wide, direction="long", idvar="pid",
varying=list(c(sprintf("age%02d", c(1:t))),
c(sprintf("income%02d", c(0:(t-1)))),
c(sprintf("event%02d", c(1:t)))),
v.names=c("age", "income", "event"), drop=c("income05"))
data_long[order(data_long$pid),]
data_wide$income00 <- NA # 観察期間前のラグ変数の準備
data_long <- reshape(data_wide, direction="long", idvar="pid",
varying=list(c(sprintf("age%02d", c(1:t))),
c(sprintf("income%02d", c(0:(t-1)))),
c(sprintf("event%02d", c(1:t)))),
v.names=c("age", "income", "event"), drop=c("income05"))
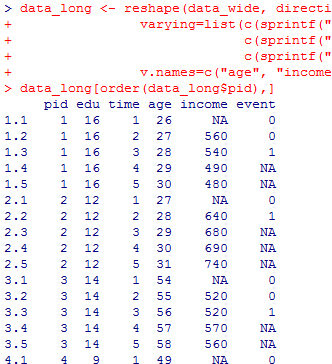
data_long[order(data_long$pid),]
なお，必要があるかどうかわからないが，reshape( )関数は，ワイド型からロング型への変換も可能である。v.names=で時間依存変数を指定すると，それ以外の変数は時間不変変数だとみなされる。不要な変数は後から列削除するとよい。
# longからwideへの変換
data_wide2 <- reshape(data_long, idvar="pid", direction="wide",
v.names=c("age","income","event"))
(data_wide3 <- data_wide2[,c(1:3, 5, 7:8, 10:11, 13:14, 16:17)]) # 必要な列のみ残す
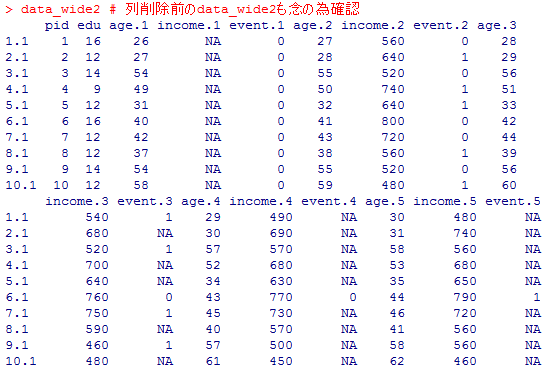
data_wide2 # 列削除前のdata_wide2も念の為確認
data_wide2 <- reshape(data_long, idvar="pid", direction="wide",
v.names=c("age","income","event"))
(data_wide3 <- data_wide2[,c(1:3, 5, 7:8, 10:11, 13:14, 16:17)]) # 必要な列のみ残す
data_wide2 # 列削除前のdata_wide2も念の為確認
2-2 離散時間ロジスティック回帰モデル(discrete-time logistic regression)
本文でも書いた様に，離散時間ロジットモデルの分析では，ロング形式データの作成が一番大変な部分で，それが出来れば分析は簡単に行われる。
以下では，n <- 30 としてデータを生成し直した上で，分析を行った結果を紹介する。
残差逸脱度が83.858，推定されるパラメタが切片を含んで4つなので，AIC=83.858+2*4=91.858となっている。
以下では，パラメタ推定値からオッズ比を計算して，要因の効果を把握している。
以下では，n <- 30 としてデータを生成し直した上で，分析を行った結果を紹介する。
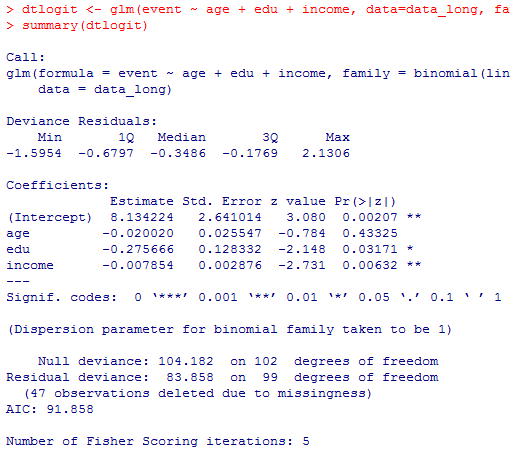
dtlogit <- glm(event ~ age + edu + income, data=data_long, family=binomial(link="logit"))
summary(dtlogit)
summary(dtlogit)
残差逸脱度が83.858，推定されるパラメタが切片を含んで4つなので，AIC=83.858+2*4=91.858となっている。
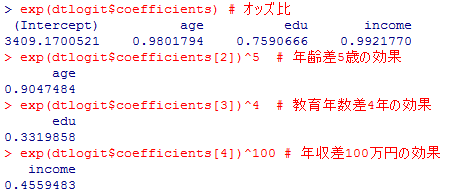
以下では，パラメタ推定値からオッズ比を計算して，要因の効果を把握している。
exp(dtlogit$coefficients) # オッズ比
exp(dtlogit$coefficients[2])^5 # 年齢差5歳の効果
exp(dtlogit$coefficients[3])^4 # 教育年数差4年の効果
exp(dtlogit$coefficients[4])^100 # 年収差100万円の効果
exp(dtlogit$coefficients[2])^5 # 年齢差5歳の効果
exp(dtlogit$coefficients[3])^4 # 教育年数差4年の効果
exp(dtlogit$coefficients[4])^100 # 年収差100万円の効果
発展1 マルチレヴェルロジットモデル(multilevel logit model)
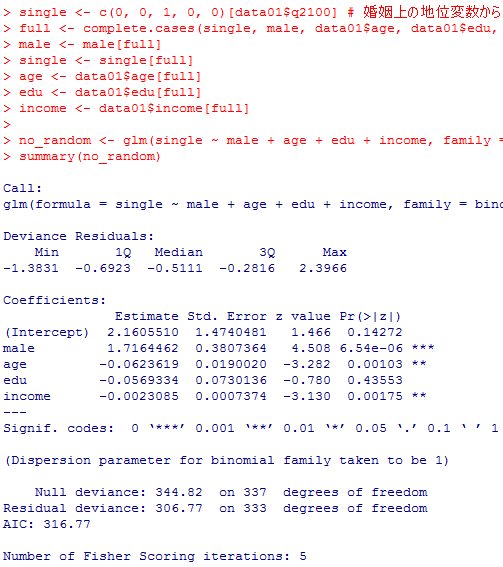
第12章1-3の，未婚オッズに対する二項ロジットモデルの分析を再掲する。
次に，地点変数siteを作成して完備ケース分析用に選択した後，lme4パッケイジのglmer( )関数を用いて，マルチレヴェルロジット分析を行ってみる。地点によって切片が異なると云うランダム切片モデルである。
結果を見比べると，パラメタ推定値は殆ど変わっておらず，AICはむしろ若干悪化している。最後に警告も出力されている通り，このモデルは余り良いモデルとは言えないが，関数の紹介やスクリプトの書き方の例としてあげた。
最後に，固定効果も変量効果も含まない切片のみのモデルをglm( )で分析して基準とし，変量効果有りのマルチレヴェルロジットモデルと変量効果無しのロジットモデルの疑似決定係数を比較してみよう。
AICが悪化していることからも想像されるように，ほとんど改善していない。あくまでこれは例示でしかないと云う事である。
male <- c(1, 0)[data01$sex] # 男性ダミーの作成
single <- c(0, 0, 1, 0, 0)[data01$q2100] # 婚姻上の地位変数から未婚ダミー作成
full <- complete.cases(single, male, data01$age, data01$edu, data01$income) # 欠損値除外
male <- male[full]
single <- single[full]
age <- data01$age[full]
edu <- data01$edu[full]
income <- data01$income[full]
no_random <- glm(single ~ male + age + edu + income, family = binomial("logit"))
summary(no_random)
single <- c(0, 0, 1, 0, 0)[data01$q2100] # 婚姻上の地位変数から未婚ダミー作成
full <- complete.cases(single, male, data01$age, data01$edu, data01$income) # 欠損値除外
male <- male[full]
single <- single[full]
age <- data01$age[full]
edu <- data01$edu[full]
income <- data01$income[full]
no_random <- glm(single ~ male + age + edu + income, family = binomial("logit"))
summary(no_random)
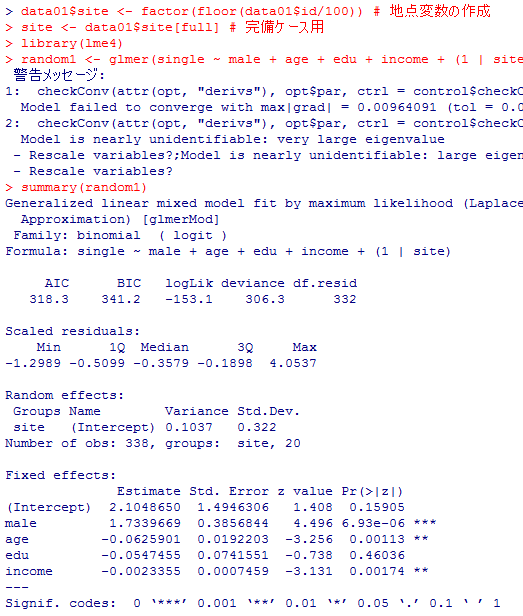
次に，地点変数siteを作成して完備ケース分析用に選択した後，lme4パッケイジのglmer( )関数を用いて，マルチレヴェルロジット分析を行ってみる。地点によって切片が異なると云うランダム切片モデルである。
data01$site <- factor(floor(data01$id/100)) # 地点変数の作成
site <- data01$site[full] # 完備ケース用
library(lme4)
random1 <- glmer(single ~ male + age + edu + income + (1 | site), family = binomial("logit"))
summary(random1)
site <- data01$site[full] # 完備ケース用
library(lme4)
random1 <- glmer(single ~ male + age + edu + income + (1 | site), family = binomial("logit"))
summary(random1)
結果を見比べると，パラメタ推定値は殆ど変わっておらず，AICはむしろ若干悪化している。最後に警告も出力されている通り，このモデルは余り良いモデルとは言えないが，関数の紹介やスクリプトの書き方の例としてあげた。
最後に，固定効果も変量効果も含まない切片のみのモデルをglm( )で分析して基準とし，変量効果有りのマルチレヴェルロジットモデルと変量効果無しのロジットモデルの疑似決定係数を比較してみよう。
# 固定効果も変量効果も含まない切片のみのモデルを基準
null <- glm(single ~ 1, family = binomial("logit"))
Lm <- logLik(random1); L0 <- logLik(null); L1 <- logLik(no_random)
n <- length(single)
1-Lm[1]/L0[1]; 1-L1[1]/L0[1] # McFadden：変量効果有りと無し
1-(exp(L0[1])/exp(Lm[1]))^(2/n) # Cox & Snell：変量効果有り
1-(exp(L0[1])/exp(L1[1]))^(2/n) # Cox & Snell：変量効果無し
(1-(exp(L0[1])/exp(Lm[1]))^(2/n))/(1-exp(L0[1])^(2/n)) # Nagelkerke：変量効果有り
(1-(exp(L0[1])/exp(L1[1]))^(2/n))/(1-exp(L0[1])^(2/n)) # Nagelkerke：変量効果無し
null <- glm(single ~ 1, family = binomial("logit"))
Lm <- logLik(random1); L0 <- logLik(null); L1 <- logLik(no_random)
n <- length(single)
1-Lm[1]/L0[1]; 1-L1[1]/L0[1] # McFadden：変量効果有りと無し
1-(exp(L0[1])/exp(Lm[1]))^(2/n) # Cox & Snell：変量効果有り
1-(exp(L0[1])/exp(L1[1]))^(2/n) # Cox & Snell：変量効果無し
(1-(exp(L0[1])/exp(Lm[1]))^(2/n))/(1-exp(L0[1])^(2/n)) # Nagelkerke：変量効果有り
(1-(exp(L0[1])/exp(L1[1]))^(2/n))/(1-exp(L0[1])^(2/n)) # Nagelkerke：変量効果無し
AICが悪化していることからも想像されるように，ほとんど改善していない。あくまでこれは例示でしかないと云う事である。
発展2 統計的因果推論(statistical causal inference)
因果推論の根本問題(fundamental problem of causal inference, FPCI)
統計学者Donald B. Rubinの基本的な考え方(Rubin's Model)として彼の教え子のPaul W. Hollandが定式化した(Paul W. Holland, 1986, 'Statistics and Causal Inference')。重要な考えであるので，これをごく簡単に概説しよう（RCM; Rubin Causal Modelとも呼ばれている）。我々が「因果関係＝原因(cause)と結果(effect, outcome)の関係」と呼ぶのは，例えば「Aさんは，有名大学を卒業した*ので*，高い収入を得られる様になった」と云った考えに表現されている関係である。有名大学卒業が高収入の「原因」であると我々が呼ぶのは，それ（原因＝有名大学卒業）が無ければ「結果（＝高収入）」が生じなかったと考えるからである。もしも，Aさんは有名大学を卒業しようが高卒後に直ぐに就職しようが同じく高い収入を得ていたであろうと我々が考えるならば，我々は「有名大学卒業」をAさんの「高収入」の原因とは呼ばないであろう。
こうした「因果関係」の言明は様々なものが有り得る。敢えて論争的な例を取り上げるならば，「長年たばこを吸っていたから肺がんになった」とか，「幼少期に特定の経験をしたから特定の性格特性が備わった」なども同じ形式であるし，個人単位でなくても，「政府支出を拡大したから（或はインフレターゲット政策を採用したから）景気が改善した」とか「積極的移民受け入れ政策を取ったから文化が繁栄した（或は政治的に不安定化した）」と云った言明も本質的に同じ形式である。いずれも，例えそれと明示していなくても，その「原因」が無ければその「結果」は無かったであろうと云う関係を想定している。個人単位の因果関係はしばしば計量的分析によってアプローチされるのに対して，国・社会を単位とする因果関係は計量分析に足るデータが存在しない事が珍しくなく，「定性的比較分析(QCA; Qualitative Comparative Analysis)」などによってアプローチされる事が多い。しかしいずれも探究している因果関係の形式は同じであると言ってよい（本当の意味で異なる種類の研究は，原因―結果と云う関係には関心を払わないタイプの研究である）。
因果関係をこの様に捉えた時，直ちに原理的な問題が浮上する。「Aさんは有名大学を卒業したから高収入を得た，有名大学を卒業していなかったら高収入を得る事は無かっただろう」と云う主張が正しいかどうかは，Aさんが実際に有名大学を卒業している限り，最早確認のしようがない。「Aさんが有名大学を卒業しなかった場合」と云うのは反実仮想(counterfactual)であり，平行世界（パラレルワールド）であり，サイエンス・フィクションの中であれば両方を観察する事が出来る（し，我々はそうした作品に余りにも親しみ過ぎていて違和感を持たない）が，現実には決して観察出来ない状態・得る事の出来ない情報なのである。これは上に例示した因果関係についての主張の全てに共通する原理的困難であり，「因果推論の根本問題」と呼ばれている。
この根本問題に直面して，だったらそんな無理な事やーめたと云って因果推論，因果関係の主張を全て放棄してしまうと云うのは一つの有り得る（潔い？）態度かも知れないが，実際には大抵の我々の思考は，余り自覚していなくても，隅々にまで「因果的思考」が行き渡っており，問題があろうがなかろうが，原理的に可能であろうが不可能であろうが，我々は因果関係を考え，因果的言明を主張している。だとすると，原理的に困難な問題を何とか近似的にでも解決もしくは対処出来ないだろうかと考えるのが，社会科学的もしくは人間行動学的な因果的探究であり，（因果）説明的研究(explanatory study)である。
因果効果(Causal Effect)
Aさんが大卒であった現実の場合の収入額(観察されたpotential outcome)と，Aさんが高卒であった反実仮想の場合の収入額(観察されないpotential outcome)が分かれば，その差額が大卒であった事の帰結，収入と云う結果に対する大卒と云う要因の因果的効果(effect of cause)と考える事が出来る。下の表で，黒の背景に白の文字の情報は原理的に観測不能（欠測; missing）であり，薄い灰色の背景に黒の文字の情報だけが実際に得られる。Aさんについての個別因果効果(ICE; Individual Causal Effect）を考えると，ICE = Yt(A) - Yc(A) となるが，計算する事は出来ない。
| 大卒のAさん | 高卒の場合の収入: Yc(A) | 大卒の場合の収入: Yt(A) |
Aさんとは大卒か高卒かが異なる以外は極めてよく似ているBさんを見付けられれば，Aさんが高卒だった場合の（＝反実仮想なので原理的にmissingな）収入の代わりに，Bさんの収入を観測する事が出来る。二つの収入の差額が，高卒か大卒かと云う要因による収入への因果効果と見做せるのではないか。
ICEの有り得る近似 ICE ≒ Yt(A) - Yc(B)
| 大卒のAさん | 高卒の場合の収入: Yc(A) | 大卒の場合の収入: Yt(A) |
| 高卒のBさん | 高卒の場合の収入: Yc(B) | 大卒の場合の収入: Yt(B) |
しかし実際には，高卒か大卒かの1点以外は全く同じ人を見付けて来る事が不可能なのは勿論，その一点を除いて極めてよく似ている人もそう簡単には見付けられない。よって他の要因による違い（誤差）を考える必要がある。誤差の影響を無くす為に，出来るだけ多くのペアを作る事を考える。
| 大卒のA1さん | 高卒の場合の収入: Yc(A1) | 大卒の場合の収入: Yt(A1) |
| 高卒のB1さん | 高卒の場合の収入: Yc(B1) | 大卒の場合の収入: Yt(B1) |
| 大卒のA2さん | 高卒の場合の収入: Yc(A2) | 大卒の場合の収入: Yt(A2) |
| 高卒のB2さん | 高卒の場合の収入: Yc(B2) | 大卒の場合の収入: Yt(B2) |
| 大卒のA3さん | 高卒の場合の収入: Yc(A3) | 大卒の場合の収入: Yt(A3) |
| 高卒のB3さん | 高卒の場合の収入: Yc(B3) | 大卒の場合の収入: Yt(B3) |
| 大卒のA4さん | 高卒の場合の収入: Yc(A4) | 大卒の場合の収入: Yt(A4) |
| 高卒のB4さん | 高卒の場合の収入: Yc(B4) | 大卒の場合の収入: Yt(B4) |
一定の条件が満たされるならば，実際には大卒の人達の，観測不能な高卒での収入の平均μc(A)は，実際に高卒の人達の観測される収入の平均μc(B)にほぼ等しいと考える事が出来る。同様に，実際には高卒の人達の，観測不能な大卒での収入の平均μt(B)は，実際に大卒の人達の観測される収入の平均μt(A)にほぼ等しいと考える事が出来る（かも知れない）。これを平均因果効果(ACE; Average Causal Effect)と呼ぶ。
ACE ≒ μt(A) - μc(B)
| 大卒のA1さん | 高卒の場合の収入の平均 μc(A) | 大卒の場合の収入平均 μt(A) |
| 大卒のA2さん | ||
| 大卒のA3さん | ||
| 大卒のA4さん | ||
| 高卒のB1さん | 高卒の場合の収入平均 μc(B) | 大卒の場合の収入平均 μt(B) |
| 高卒のB2さん | ||
| 高卒のB3さん | ||
| 高卒のB4さん |
勿論，問題は，この近似がどうしたら成立するかを適切に解明する事であり，実験研究(experimental study)ではなく観察研究(observational study)ではこの点が非常に重要になるが，話が難しくなるのでここでは割愛する。
Both QUAN and QUAL
Charles C. Raginのブール代数分析，ファジー集合理論などを典型とする定性的比較研究(QCA)の研究戦略と統計的因果推論を比較・検討する事は，単に「質／量」と分割・対置する態度を超えてそれぞれを深く理解する為に非常に有効ではないかと考える。記述(description)と説明(explanation)，相関(correlation)と因果(causation)，caseとは何か('What is a Case?', 'What is this a case of ?')，全体もしくは母集団と一部分もしくは標本，caseはどの様に選ぶべきなのか(case selection, sampling method)，複数の・競合する理論や説明の尤もらしさの比較，理論や説明の尤もらしさの変化・更新(Bayesian Theory)，単一事例研究(single case study)と複数事例研究(multiple case study)など，“量的”研究であれ“質的”研究であれ考えずに済ます事の出来ない共通の準拠問題は数多くあり，同じ問題に対する異なった・別の対処法として理解していく事をここでは推奨する。
Copyright (C) 2016-2017 SUGINO Isamu All Rights Reserved. design by tempnate