杉野 勇 (SUGINO Isamu) お茶の水女子大学・人間発達科学専攻・応用社会学コース担当
『入門・社会統計学』サポートウェブ |
第8章 単回帰分析(SRA)
1-1 最小二乗和法(Least Squares Method)
本文では式変形について丁寧に示せなかったので，ここでより詳しいPDFを上げておく。まずは最小二乗和法の式変形について。
次に，残差の平均や，残差と独立変数の共分散，残差と予測値の共分散が0になる事について。
次に，残差の平均や，残差と独立変数の共分散，残差と予測値の共分散が0になる事について。
1-2 回帰係数(regression coefficient)のt検定と区間推定(interval estimation)
このサポートウェブではデータフレイム名をdata01としているので注意されたい。世帯年収で幸福度を説明する単回帰モデルの分析結果は以下の通りである。
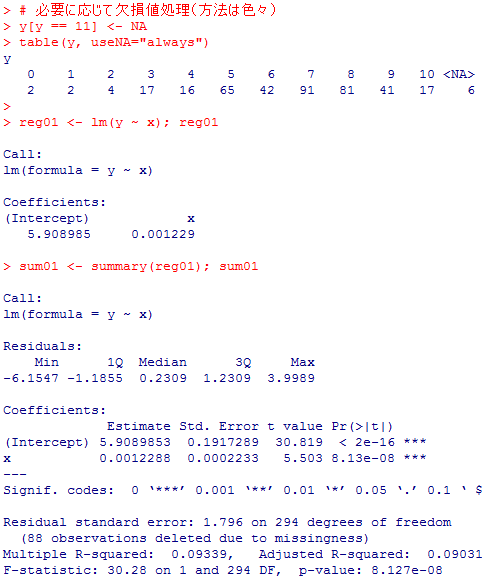
それぞれのオブジェクトにどの様な情報が格納されているのか名前を確認しておく。序に，定数項と回帰係数のt検定の両側有意確率を求めておく。
結果を見比べて，正しく計算出来ている事が確認出来る。
最後に，定数項や回帰係数の信頼区間の求め方を示す。最初は定義に従って自分で式を組み立てて求める方法，次にconfint( )関数によって自動的に求める方法である。
対応する箇所をよく見比べて欲しい。
母回帰係数の95%信頼区間が.00079から.00167であると云う事は，有意水準5%で母回帰係数のt検定を行った場合，ゼロ仮説「母回帰係数は.00079である」から「母回帰係数は.00167である」までのゼロ仮説はどれも棄却されないと云う事でもある。区間に0を含んでいないので，「母回帰係数は0である」は棄却される。これは先の回帰係数のt検定の結果の通りである。
x <- data01$fincome
y <- data01$q1700
# まずは変数の分布を確認しておく
table(x, useNA="always")
table(y, useNA="always")
# 必要に応じて欠損値処理（方法は色々）
y[y == 11] <- NA
table(y, useNA="always")
reg01 <- lm(y ~ x); reg01
sum01 <- summary(reg01); sum01
y <- data01$q1700
# まずは変数の分布を確認しておく
table(x, useNA="always")
table(y, useNA="always")
# 必要に応じて欠損値処理（方法は色々）
y[y == 11] <- NA
table(y, useNA="always")
reg01 <- lm(y ~ x); reg01
sum01 <- summary(reg01); sum01
それぞれのオブジェクトにどの様な情報が格納されているのか名前を確認しておく。序に，定数項と回帰係数のt検定の両側有意確率を求めておく。
names(reg01) # lm( )関数の結果
names(sum01) # summary( )関数の結果
reg01$coefficients
sum01$coefficients
sum01$df
# オブジェクトsum01に含まれる情報からt統計量を計算し，t検定を行う。
t0 <- sum01$coefficients[,1]/sum01$coefficients[,2]; t0
2*pt(t0, df=sum01$df[2], lower.tail=F) # 両側t検定の有意確率
names(sum01) # summary( )関数の結果
reg01$coefficients
sum01$coefficients
sum01$df
# オブジェクトsum01に含まれる情報からt統計量を計算し，t検定を行う。
t0 <- sum01$coefficients[,1]/sum01$coefficients[,2]; t0
2*pt(t0, df=sum01$df[2], lower.tail=F) # 両側t検定の有意確率
結果を見比べて，正しく計算出来ている事が確認出来る。
最後に，定数項や回帰係数の信頼区間の求め方を示す。最初は定義に従って自分で式を組み立てて求める方法，次にconfint( )関数によって自動的に求める方法である。
# 自由度と，t分布の限界値を確認
sum01$df[2]; qt(.975, df=sum01$df[2])
# 95%信頼区間下限
sum01$coefficients[,1]-qt(.975, df=sum01$df[2])*sum01$coefficients[,2]
# 95%信頼区間上限
sum01$coefficients[,1]+qt(.975, df=sum01$df[2])*sum01$coefficients[,2]
# 信頼区間を求める関数
confint(reg01, level=.95)
sum01$df[2]; qt(.975, df=sum01$df[2])
# 95%信頼区間下限
sum01$coefficients[,1]-qt(.975, df=sum01$df[2])*sum01$coefficients[,2]
# 95%信頼区間上限
sum01$coefficients[,1]+qt(.975, df=sum01$df[2])*sum01$coefficients[,2]
# 信頼区間を求める関数
confint(reg01, level=.95)
対応する箇所をよく見比べて欲しい。
母回帰係数の95%信頼区間が.00079から.00167であると云う事は，有意水準5%で母回帰係数のt検定を行った場合，ゼロ仮説「母回帰係数は.00079である」から「母回帰係数は.00167である」までのゼロ仮説はどれも棄却されないと云う事でもある。区間に0を含んでいないので，「母回帰係数は0である」は棄却される。これは先の回帰係数のt検定の結果の通りである。
1-3 回帰モデルのF検定
分散分析表を作成する為に，anova( )関数を使用する。
総平方和が従属変数の偏差平方和である事が確認出来た。
単回帰分析においては，回帰係数のt検定とモデルのF検定は同値である事を以下で示す。
# lm( )の結果であるreg01をanova( )に与える。
ano01 <- anova(reg01); ano01
names(ano01) # 格納されている情報を確認
ano01$"Sum Sq" # 偏差平方和だけを取り出す
sum(ano01$"Sum Sq") # 総平方和を計算する
# 総平方和が，従属変数の偏差平方和である事を確認する
# xかyにNAを含むケースを全て除外して完備ケースだけにしないと結果が一致しなくなるので注意
sum((y[complete.cases(y, x)]-mean(y[complete.cases(y, x)]))^2)
ano01 <- anova(reg01); ano01
names(ano01) # 格納されている情報を確認
ano01$"Sum Sq" # 偏差平方和だけを取り出す
sum(ano01$"Sum Sq") # 総平方和を計算する
# 総平方和が，従属変数の偏差平方和である事を確認する
# xかyにNAを含むケースを全て除外して完備ケースだけにしないと結果が一致しなくなるので注意
sum((y[complete.cases(y, x)]-mean(y[complete.cases(y, x)]))^2)
総平方和が従属変数の偏差平方和である事が確認出来た。
| 平方和 | 自由度 | 平均平方 | F値 | p値 | |
| 定数項 | 97.72471 | 1 | 97.72471 | 30.28453 | <.001 |
| 独立変数 | 948.70435 | 294 | 3.226886 | ||
| 合計 | 1046.42906 | 295 |
単回帰分析においては，回帰係数のt検定とモデルのF検定は同値である事を以下で示す。
# 回帰係数のt検定の結果の一部
names(sum01)
sum01$coefficients
(t0 <- sum01$coefficients[2, 3]) # t統計量
t0^2 # t統計量の二乗
# モデルのF検定の結果の一部
names(ano01)
ano01$"F value"[1] # F統計量
sum01$coefficients[2, 4] # t検定のp値
ano01$"Pr(>F)"[1] # F検定のp値
names(sum01)
sum01$coefficients
(t0 <- sum01$coefficients[2, 3]) # t統計量
t0^2 # t統計量の二乗
# モデルのF検定の結果の一部
names(ano01)
ano01$"F value"[1] # F統計量
sum01$coefficients[2, 4] # t検定のp値
ano01$"Pr(>F)"[1] # F検定のp値
1-4 決定係数(coefficient of determinance)，分散説明率(proportion of variance explained)，誤差減少率(PRE)
決定係数（分散説明率）を幾通りかの方法で確認してみよう。
lm( )関数をanova( )関数に引き渡した結果であるano01の情報から分散説明率を計算した結果は，lm( )関数をsummary( )関数に引き渡した結果であるsum01が表示する分散説明率(Multiple R-squared)に一致している。自由度調整済み分散説明率(Adjusted R-squared)は無調整の分散説明率より小さい。これは母集団における分散説明率の推定値である。
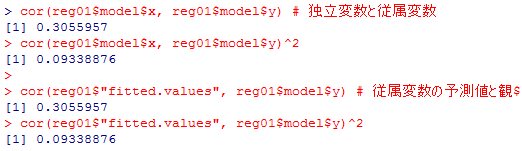
従属変数の観測値（完備ケースに限定）とその予測値(fitted.values)の積率相関係数は約.3056，その二乗は分散説明率に一致する。また，従属変数（観測値）と独立変数の積率相関係数R1はR0に一致する。予測値は独立変数の一次変換であり，積率相関係数は一次変換に関して（絶対値）不変である事を考えれば理解出来る筈である。
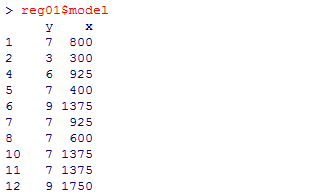
実はlm( )関数の結果であるreg01は，"model"という名前で，分析に用いられた独立変数と従属変数のデータを格納しているので，これを用いる方が相関係数の計算はスマートに出来る。
ano01$"Sum Sq"[1] # モデル平方和
sum(ano01$"Sum Sq") # 総平方和
ano01$"Sum Sq"[1]/sum(ano01$"Sum Sq") # 分散説明率
sum01 # Multiple R-squared と Adjusted R-squared に注目
# 観測値と予測値の相関係数，その二乗
names(reg01)
R0 <- cor(y[complete.cases(y, x)], reg01$"fitted.values"); R0
R0^2
# 観測値と独立変数，その二乗
R1 <- cor(y[complete.cases(y, x)], x[complete.cases(y, x)]); R1
R1^2
sum(ano01$"Sum Sq") # 総平方和
ano01$"Sum Sq"[1]/sum(ano01$"Sum Sq") # 分散説明率
sum01 # Multiple R-squared と Adjusted R-squared に注目
# 観測値と予測値の相関係数，その二乗
names(reg01)
R0 <- cor(y[complete.cases(y, x)], reg01$"fitted.values"); R0
R0^2
# 観測値と独立変数，その二乗
R1 <- cor(y[complete.cases(y, x)], x[complete.cases(y, x)]); R1
R1^2
lm( )関数をanova( )関数に引き渡した結果であるano01の情報から分散説明率を計算した結果は，lm( )関数をsummary( )関数に引き渡した結果であるsum01が表示する分散説明率(Multiple R-squared)に一致している。自由度調整済み分散説明率(Adjusted R-squared)は無調整の分散説明率より小さい。これは母集団における分散説明率の推定値である。
従属変数の観測値（完備ケースに限定）とその予測値(fitted.values)の積率相関係数は約.3056，その二乗は分散説明率に一致する。また，従属変数（観測値）と独立変数の積率相関係数R1はR0に一致する。予測値は独立変数の一次変換であり，積率相関係数は一次変換に関して（絶対値）不変である事を考えれば理解出来る筈である。
実はlm( )関数の結果であるreg01は，"model"という名前で，分析に用いられた独立変数と従属変数のデータを格納しているので，これを用いる方が相関係数の計算はスマートに出来る。
cor(reg01$model$x, reg01$model$y) # 独立変数と従属変数
cor(reg01$model$x, reg01$model$y)^2
cor(reg01$"fitted.values", reg01$model$y) # 従属変数の予測値と観測値
cor(reg01$"fitted.values", reg01$model$y)^2
cor(reg01$model$x, reg01$model$y)^2
cor(reg01$"fitted.values", reg01$model$y) # 従属変数の予測値と観測値
cor(reg01$"fitted.values", reg01$model$y)^2
2-1 相関係数と回帰係数
標本相関係数と標本回帰係数の関係を確認する。
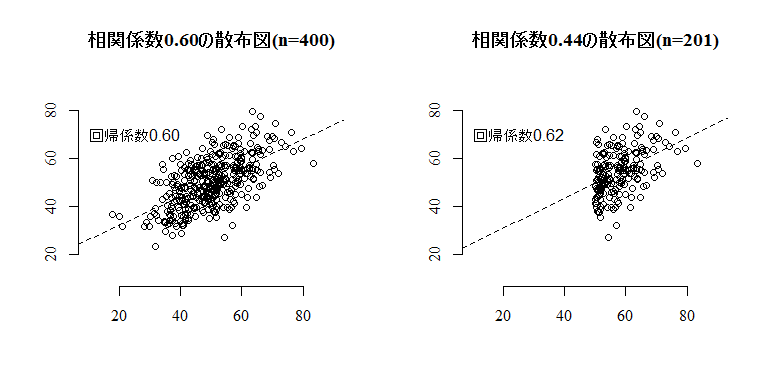
ここで，本文の様に選抜効果を確認するグラフを描くスクリプトを紹介する。設定した相関係数にぴたりと一致するヴェクトル対の作成法などは単回帰分析や合成変数の分散・共分散について深い理解を必要とするので難しく，理解出来なくても支障無いが，グラフの描き方などは知っておくと色々と便利な工夫が含まれている。
シミュレイションなので，実行するたびに多少異なった結果になる。回帰係数が殆ど変化しない場合もあれば，大きく変化する場合もある。
reg01$coefficients[2] # 標本回帰係数
# 標本相関係数R1とx,yの標準偏差から計算
R1*sd(y[complete.cases(y, x)])/sd(x[complete.cases(y, x)])
# sd( )は不偏分散の平方根なので，標本標準偏差から計算する
yc <- y[complete.cases(y, x)] # 完備ケースだけを新変数に
xc <- x[complete.cases(y, x)]
# 分散は偏差平方の平均である事を利用
R1*sqrt(mean((yc-mean(yc))^2))/sqrt(mean((xc-mean(xc))^2))
# 標本相関係数R1とx,yの標準偏差から計算
R1*sd(y[complete.cases(y, x)])/sd(x[complete.cases(y, x)])
# sd( )は不偏分散の平方根なので，標本標準偏差から計算する
yc <- y[complete.cases(y, x)] # 完備ケースだけを新変数に
xc <- x[complete.cases(y, x)]
# 分散は偏差平方の平均である事を利用
R1*sqrt(mean((yc-mean(yc))^2))/sqrt(mean((xc-mean(xc))^2))
ここで，本文の様に選抜効果を確認するグラフを描くスクリプトを紹介する。設定した相関係数にぴたりと一致するヴェクトル対の作成法などは単回帰分析や合成変数の分散・共分散について深い理解を必要とするので難しく，理解出来なくても支障無いが，グラフの描き方などは知っておくと色々と便利な工夫が含まれている。
r <- .60 # 選抜前の相関係数を任意に設定
n <- 400 # ケース数を任意に設定
y <- rnorm(n, mean=0, sd=1)
x0 <- rnorm(n, mean=0, sd=1)
x <- scale(x0)
e0 <- lm(y ~ x)$residuals
e <- scale(e0)
u <- sqrt(1-r^2)*e + r*x
cor(x, u) # 設定した相関係数にぴたりと一致するヴェクトル対が出来た
X <- x*10 + 50 # 偏差値化
U <- u*10 + 50
cor(X, U) # 相関係数は当然変わっていない
b <- lm(U ~ X)$coefficients[2] # 回帰係数をbに格納
windows(width=8, height=4) # 描画ウィンドウの大きさ指定
par(mfrow=c(1, 2)) # ウィンドウを1行2列に分割
# 選抜のない散布図
plot(X, U, bty="n", family="serif",
main=sprintf("相関係数%.2fの散布図(n=%d)", r, n),
xlab="", ylab="", xlim=c(10, 90), ylim=c(10, 90))
abline(lm(U ~ X), lty=2) # 回帰直線を点線で書き込む
text(25, 70, sprintf("回帰係数%.2f", b))
# 選抜のある散布図
X1 <- X[X >= 50]; U1 <- U[X >= 50]
r1 <- cor(X1, U1); n1 <- length(X1)
b1 <- lm(U1 ~ X1)$coefficients[2]
plot(X1, U1, bty="n", family="serif",
main=sprintf("相関係数%.2fの散布図(n=%d)", r1, n1),
xlab="", ylab="", xlim=c(10, 90), ylim=c(10, 90))
abline(lm(U1 ~ X1), lty=2) # 回帰直線を点線で書き込む
text(25, 70, sprintf("回帰係数%.2f", b1))
n <- 400 # ケース数を任意に設定
y <- rnorm(n, mean=0, sd=1)
x0 <- rnorm(n, mean=0, sd=1)
x <- scale(x0)
e0 <- lm(y ~ x)$residuals
e <- scale(e0)
u <- sqrt(1-r^2)*e + r*x
cor(x, u) # 設定した相関係数にぴたりと一致するヴェクトル対が出来た
X <- x*10 + 50 # 偏差値化
U <- u*10 + 50
cor(X, U) # 相関係数は当然変わっていない
b <- lm(U ~ X)$coefficients[2] # 回帰係数をbに格納
windows(width=8, height=4) # 描画ウィンドウの大きさ指定
par(mfrow=c(1, 2)) # ウィンドウを1行2列に分割
# 選抜のない散布図
plot(X, U, bty="n", family="serif",
main=sprintf("相関係数%.2fの散布図(n=%d)", r, n),
xlab="", ylab="", xlim=c(10, 90), ylim=c(10, 90))
abline(lm(U ~ X), lty=2) # 回帰直線を点線で書き込む
text(25, 70, sprintf("回帰係数%.2f", b))
# 選抜のある散布図
X1 <- X[X >= 50]; U1 <- U[X >= 50]
r1 <- cor(X1, U1); n1 <- length(X1)
b1 <- lm(U1 ~ X1)$coefficients[2]
plot(X1, U1, bty="n", family="serif",
main=sprintf("相関係数%.2fの散布図(n=%d)", r1, n1),
xlab="", ylab="", xlim=c(10, 90), ylim=c(10, 90))
abline(lm(U1 ~ X1), lty=2) # 回帰直線を点線で書き込む
text(25, 70, sprintf("回帰係数%.2f", b1))
シミュレイションなので，実行するたびに多少異なった結果になる。回帰係数が殆ど変化しない場合もあれば，大きく変化する場合もある。
2-2 標準化回帰係数(standardized regression coefficient)
このサポートウェブでは既に活用して来た手法だが，変数をそれぞれ単独で欠損値除外するのではなく，使用する変数全てが有効であるケースだけを残さないと，多変量解析の結果が正しく再現出来ない恐れがある。こうした分析は「完備ケース分析」といい，欠損分析の観点からは決して問題が無いとは言えないが，初歩的分析では広く使用されている。
標準化偏回帰係数を求める場合にも，完備ケースだけを選び出した後で独立変数と従属変数を標準化しないと正しい結果が得られなくなる。
本文同様，まずは独立変数と従属変数を単純にそれぞれ標準化して単回帰分析を行った結果を示す。
標準化されているので独立変数も従属変数も平均は0の筈であり，回帰直線は点（xの平均，yの平均）を通る筈なので，この場合原点を通る筈である。しかし定数項（切片）が誤差の範囲で0に一致しない。また，xの標準偏差とyの標準偏差は共に1である筈なので，回帰係数は積率相関係数に一致し，その値は.3056であると既に求められているが，ここでの回帰係数は.3039でやはりずれている。これらから，適切な変換がなされていない事が分かる。
正しくは，以下の様にする。
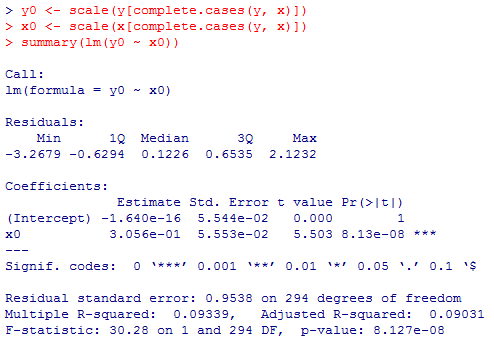
切片は（誤差の範囲で）0となり，回帰係数も上で求めた積率相関係数に一致している。
標準化偏回帰係数を求める場合にも，完備ケースだけを選び出した後で独立変数と従属変数を標準化しないと正しい結果が得られなくなる。
本文同様，まずは独立変数と従属変数を単純にそれぞれ標準化して単回帰分析を行った結果を示す。
標準化されているので独立変数も従属変数も平均は0の筈であり，回帰直線は点（xの平均，yの平均）を通る筈なので，この場合原点を通る筈である。しかし定数項（切片）が誤差の範囲で0に一致しない。また，xの標準偏差とyの標準偏差は共に1である筈なので，回帰係数は積率相関係数に一致し，その値は.3056であると既に求められているが，ここでの回帰係数は.3039でやはりずれている。これらから，適切な変換がなされていない事が分かる。
正しくは，以下の様にする。
切片は（誤差の範囲で）0となり，回帰係数も上で求めた積率相関係数に一致している。
発展1 2群の母平均の差のt検定と単回帰分析
性別と幸福度のスチューデントのt検定の結果を確認しておこう。
次に，男性ダミー変数を作成して単回帰分析を行う。
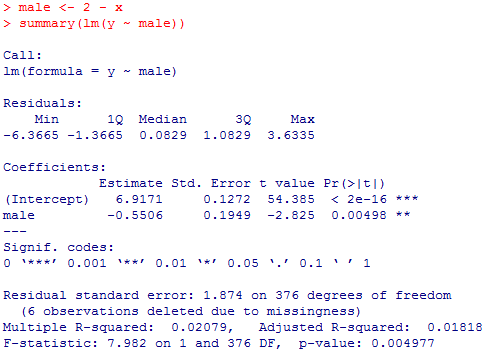
F統計量は上のt統計量の二乗に一致し，両者の有意確率も.004977で一致している。t統計量の自由度とF統計量の自由度2も勿論一致している。
単回帰分析のCoefficientsのEstimateの(Intercept)はt検定の出力における女性の平均値6.917051と（四捨五入の範囲で）一致している。男性ダミー変数の係数である-.5506は，t検定の出力における男性平均マイナス女性平均の-.550591に（四捨五入の範囲で）一致する。よく見るとその回帰係数のt検定のt統計量と有意確率も，上の二群の母平均の差のt検定におけるt統計量と有意確率に一致している。単回帰であるから，回帰係数のt検定とモデルのF検定は実質的に同じであり，そしてそれらは二群の母平均差のt検定と実質的に同じなのである。数式表現については本文を参照して欲しい。
ここでは，回帰分析による検定・推定が妥当である為のこれらの条件のチェックの方法として，残差プロット(Residuals plot)による回帰診断(regression diagnostics)を紹介する。
本章の1-2の，世帯年収で11段階幸福度を説明する単回帰の結果について，残差による診断を例示する。以下のスクリプトは，最後を除いては，実質的に1-2の再掲である。R Consoleの出力は省略し，図のみ掲載する。
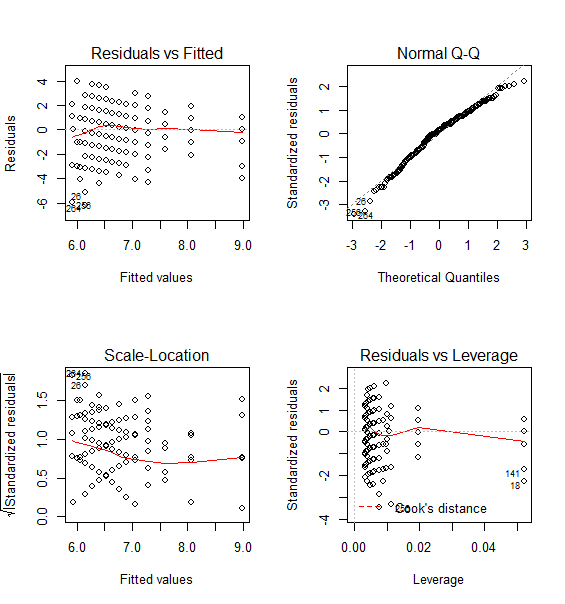
このグラフの見方について，詳しくは以下のサイトなどを参照すると良い。
University of Virginia Library, Research Data Services + Sciences, 'Understanding Diagnostic Plots for Linear Regression Analysis'(2016年12月24日閲覧)
簡単に言えば，まず?左上の'Residuals vs Fitted'プロットで，各予測値(fitted value)ごとの残差が，適切に線型パタンを示しているかどうかをチェックする。大体水平に近い赤い線が引かれれば問題無い。
次に右上の?'Normal Q-Q'プロット（正規確率プロット）で，残差の正規性が満たされているかどうかをチェックする。ほぼ45°線上に並んでいれば，理論的な正規分布からのずれが大きくないのでOKである。
左下の?'Scale-Location'では，等分散性のチェックが行われている。どの予測値に対しても，同じ様に「標準化残差の平方根」が分布していれば問題ない。
最後に右下の?'Residuals vs Leverage'プロットでは，全体の結果に対する影響力の大きいケース(high-leverage)で大きな標準化残差を持つものがあると，それだけで全体の分析結果を大きく左右する（つまり問題を孕んだ外れ値の可能性が高い）事を示す。Leverageの高い右側の方で，Standardized residualが0から遠い点に，番号が付される。これらは，全体に対して影響力の高い点であり，それを含めた分析と除外した分析で結果が少なからず変化する事を意味している。
以上の様にして，残差と予測値に関連があるか否か?，残差が正規性を充たすか?，残差が等分散性を充たすか?，問題を孕んだ外れ値が無いか?をチェックする事が出来る。
次に，男性ダミー変数を作成して単回帰分析を行う。
F統計量は上のt統計量の二乗に一致し，両者の有意確率も.004977で一致している。t統計量の自由度とF統計量の自由度2も勿論一致している。
単回帰分析のCoefficientsのEstimateの(Intercept)はt検定の出力における女性の平均値6.917051と（四捨五入の範囲で）一致している。男性ダミー変数の係数である-.5506は，t検定の出力における男性平均マイナス女性平均の-.550591に（四捨五入の範囲で）一致する。よく見るとその回帰係数のt検定のt統計量と有意確率も，上の二群の母平均の差のt検定におけるt統計量と有意確率に一致している。単回帰であるから，回帰係数のt検定とモデルのF検定は実質的に同じであり，そしてそれらは二群の母平均差のt検定と実質的に同じなのである。数式表現については本文を参照して欲しい。
等分散正規性など，残差に要求される前提について
以上で，Studentのt検定と，ダミー変数一個を用いた単回帰分析が同値である事を示した。Studentのt検定は，Welchの検定とは異なり，等分散正規性の条件を必要とするものであった（正規性の前提については，中心極限定理があるので，大標本の場合には統計的検定は頑健(robust)であるとの議論も多いが）。従って単回帰分析でも，残差について等分散正規性が要請されているのである。その他，各測定値が独立である（系列相関やクラスタとしての類似性が無い）と云う条件も満たしている必要がある。ここでは，回帰分析による検定・推定が妥当である為のこれらの条件のチェックの方法として，残差プロット(Residuals plot)による回帰診断(regression diagnostics)を紹介する。
本章の1-2の，世帯年収で11段階幸福度を説明する単回帰の結果について，残差による診断を例示する。以下のスクリプトは，最後を除いては，実質的に1-2の再掲である。R Consoleの出力は省略し，図のみ掲載する。
x <- data01$fincome
y <- data01$q1700; y[y == 11] <- NA
sum01 <- summary(reg01 <- lm(y ~ x)); sum01
par(mfrow=c(2,2)) # 4つの診断図が出力されるので，作図領域を2行2列に分割しておく
plot(reg01) # 4つの診断図を出力する
y <- data01$q1700; y[y == 11] <- NA
sum01 <- summary(reg01 <- lm(y ~ x)); sum01
par(mfrow=c(2,2)) # 4つの診断図が出力されるので，作図領域を2行2列に分割しておく
plot(reg01) # 4つの診断図を出力する
このグラフの見方について，詳しくは以下のサイトなどを参照すると良い。
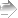University of Virginia Library, Research Data Services + Sciences, 'Understanding Diagnostic Plots for Linear Regression Analysis'(2016年12月24日閲覧)次に右上の?'Normal Q-Q'プロット（正規確率プロット）で，残差の正規性が満たされているかどうかをチェックする。ほぼ45°線上に並んでいれば，理論的な正規分布からのずれが大きくないのでOKである。
左下の?'Scale-Location'では，等分散性のチェックが行われている。どの予測値に対しても，同じ様に「標準化残差の平方根」が分布していれば問題ない。
最後に右下の?'Residuals vs Leverage'プロットでは，全体の結果に対する影響力の大きいケース(high-leverage)で大きな標準化残差を持つものがあると，それだけで全体の分析結果を大きく左右する（つまり問題を孕んだ外れ値の可能性が高い）事を示す。Leverageの高い右側の方で，Standardized residualが0から遠い点に，番号が付される。これらは，全体に対して影響力の高い点であり，それを含めた分析と除外した分析で結果が少なからず変化する事を意味している。
以上の様にして，残差と予測値に関連があるか否か?，残差が正規性を充たすか?，残差が等分散性を充たすか?，問題を孕んだ外れ値が無いか?をチェックする事が出来る。
発展2 偏相関係数(partial correlation coefficient)
ゼロ次の積率相関係数行列と，偏相関係数行列を出力する。R Commander(Rcmdr)をinstallしていない場合はインストールから行う。library(Rcmdr)でR Commanderを有効化した時に，更に追加のパッケイジを求められた場合には，指示の通りにインストールすればよい。
本文脚注でも述べたが，bookは順序尺度なので本来は間隔尺度に変換する方が良いだろうが，ここでは単純化の為にそのまま使用している。
教育年数eduを統制した場合の年収incomeと蔵書bookの偏相関係数とは，incomeをeduで説明する回帰分析の残差と，bookをeduで説明する回帰分析の残差との相関係数である。その事を以下で示そう。
library(Rcmdr)
cor(cbind("edu"=data01$edu, "income"=data01$income, "book"=data01$q0200), use="complete")
partial.cor(cbind("edu"=data01$edu, "income"=data01$income, "book"=data01$q0200), use="complete")
cor(cbind("edu"=data01$edu, "income"=data01$income, "book"=data01$q0200), use="complete")
partial.cor(cbind("edu"=data01$edu, "income"=data01$income, "book"=data01$q0200), use="complete")
本文脚注でも述べたが，bookは順序尺度なので本来は間隔尺度に変換する方が良いだろうが，ここでは単純化の為にそのまま使用している。
教育年数eduを統制した場合の年収incomeと蔵書bookの偏相関係数とは，incomeをeduで説明する回帰分析の残差と，bookをeduで説明する回帰分析の残差との相関係数である。その事を以下で示そう。
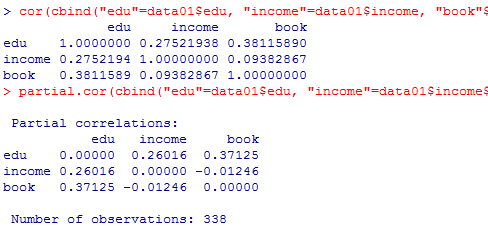
# 三つの変数が全て有効であるケースに限定する準備（完備ケース分析）
boolean <- complete.cases(data01$edu, data01$income, data01$q0200)
x <- data01$income[boolean]; y <- data01$q0200[boolean]; z <- data01$edu[boolean]
# 教育年数で年収を，教育年数で蔵書数を説明する回帰分析
summary(lmx <- lm(x ~ z)); summary(lmy <- lm(y ~ z))
# それぞれの単回帰分析の残差同士の積率相関係数
cor(lmx$residuals, lmy$residuals)
boolean <- complete.cases(data01$edu, data01$income, data01$q0200)
x <- data01$income[boolean]; y <- data01$q0200[boolean]; z <- data01$edu[boolean]
# 教育年数で年収を，教育年数で蔵書数を説明する回帰分析
summary(lmx <- lm(x ~ z)); summary(lmy <- lm(y ~ z))
# それぞれの単回帰分析の残差同士の積率相関係数
cor(lmx$residuals, lmy$residuals)
第8章の【練習問題】の解答
1) の答え：
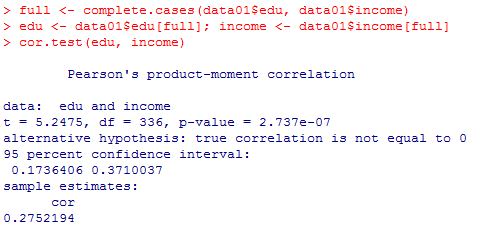
標本相関係数は.275程度（95%信頼区間は.174〜.371）であり，ゼロ仮説「母相関係数は0である」は有意水準0.1%でも棄却される。
2) の答え：
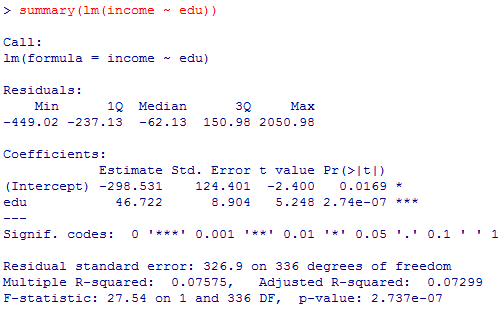
1)の相関係数のt検定と，この2)の回帰係数のt検定は一致している。t統計量5.2475の二乗は27.53626となり，F統計量27.54に一致する。自由度や有意確率も一致している。また，相関係数.2752194の二乗は.07574572で，分散説明率.07575に一致する。
3) の答え： 以下のスクリプトの結果の中に全て示されている。
4) の答え： 必要最小限なら下記のスクリプトで実行できる。
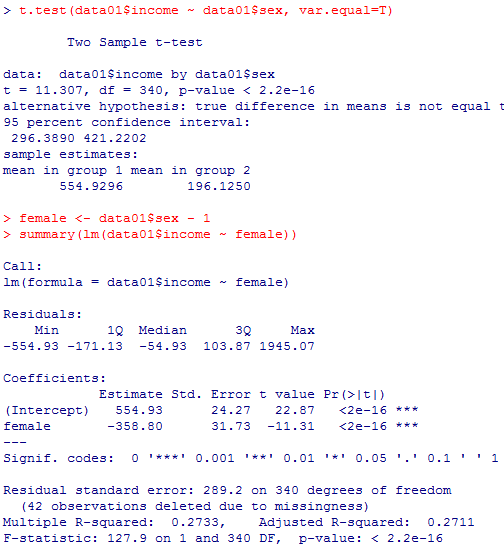
だが，それぞれの対応関係を確認する為にはやはり一旦オブジェクトに格納した方が便利である。
full <- complete.cases(data01$edu, data01$income)
edu <- data01$edu[full]; income <- data01$income[full]
cor.test(edu, income)
edu <- data01$edu[full]; income <- data01$income[full]
cor.test(edu, income)
標本相関係数は.275程度（95%信頼区間は.174〜.371）であり，ゼロ仮説「母相関係数は0である」は有意水準0.1%でも棄却される。
2) の答え：
1)の相関係数のt検定と，この2)の回帰係数のt検定は一致している。t統計量5.2475の二乗は27.53626となり，F統計量27.54に一致する。自由度や有意確率も一致している。また，相関係数.2752194の二乗は.07574572で，分散説明率.07575に一致する。
3) の答え： 以下のスクリプトの結果の中に全て示されている。
names(cor.test(edu, income))
cor.test(edu, income)$estimate
sd(edu); sd(income)
cor.test(edu, income)$estimate*sd(income)/sd(edu)
lm(income ~ edu)$coefficients[2] # 回帰係数
cor.test(edu, income)$estimate^2 # 相関係数の二乗
summary(lm(income ~ edu))$"r.squared" #分散説明
cor.test(edu, income)$estimate
sd(edu); sd(income)
cor.test(edu, income)$estimate*sd(income)/sd(edu)
lm(income ~ edu)$coefficients[2] # 回帰係数
cor.test(edu, income)$estimate^2 # 相関係数の二乗
summary(lm(income ~ edu))$"r.squared" #分散説明
4) の答え： 必要最小限なら下記のスクリプトで実行できる。
t.test(data01$income ~ data01$sex, var.equal=T)
female <- data01$sex - 1
summary(lm(data01$income ~ female))
female <- data01$sex - 1
summary(lm(data01$income ~ female))
だが，それぞれの対応関係を確認する為にはやはり一旦オブジェクトに格納した方が便利である。
t01 <- t.test(data01$income ~ data01$sex, var.equal=T)
r01 <- summary(lm(data01$income ~ female))
names(t01); names(r01)
t01$statistic^2 # t値の二乗
r01$fstatistic # F値
diff(t01$estimate) # 標本平均の差
r01$coefficients[2, 1] # 回帰係数
t01$"conf.int" # 平均値差の95%信頼区間
confint(lm(data01$income ~ female))[2, ] # 回帰係数の95%信頼区間
r01 <- summary(lm(data01$income ~ female))
names(t01); names(r01)
t01$statistic^2 # t値の二乗
r01$fstatistic # F値
diff(t01$estimate) # 標本平均の差
r01$coefficients[2, 1] # 回帰係数
t01$"conf.int" # 平均値差の95%信頼区間
confint(lm(data01$income ~ female))[2, ] # 回帰係数の95%信頼区間
Copyright (C) 2016-2017 SUGINO Isamu All Rights Reserved. design by tempnate